Information gain calculates the reduction in entropy or surprise from transforming a dataset in some way.
It is commonly used in the construction of decision trees from a training dataset, by evaluating the information gain for each variable, and selecting the variable that maximizes the information gain, which in turn minimizes the entropy and best splits the dataset into groups for effective classification.
Information gain can also be used for feature selection, by evaluating the gain of each variable in the context of the target variable. In this slightly different usage, the calculation is referred to as mutual information between the two random variables.
In this post, you will discover information gain and mutual information in machine learning.
After reading this post, you will know:
- Information gain is the reduction in entropy or surprise by transforming a dataset and is often used in training decision trees.
- Information gain is calculated by comparing the entropy of the dataset before and after a transformation.
- Mutual information calculates the statistical dependence between two variables and is the name given to information gain when applied to variable selection.
Kick-start your project with my new book Probability for Machine Learning, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
- Update Nov/2019: Improved the description of info/entropy basics (thanks HR).
- Update Aug/2020: Added missing brackets to equation (thanks David)

What is Information Gain and Mutual Information for Machine Learning
Photo by Giuseppe Milo, some rights reserved.
Overview
This tutorial is divided into five parts; they are:
- What Is Information Gain?
- Worked Example of Calculating Information Gain
- Examples of Information Gain in Machine Learning
- What Is Mutual Information?
- How Are Information Gain and Mutual Information Related?
What Is Information Gain?
Information Gain, or IG for short, measures the reduction in entropy or surprise by splitting a dataset according to a given value of a random variable.
A larger information gain suggests a lower entropy group or groups of samples, and hence less surprise.
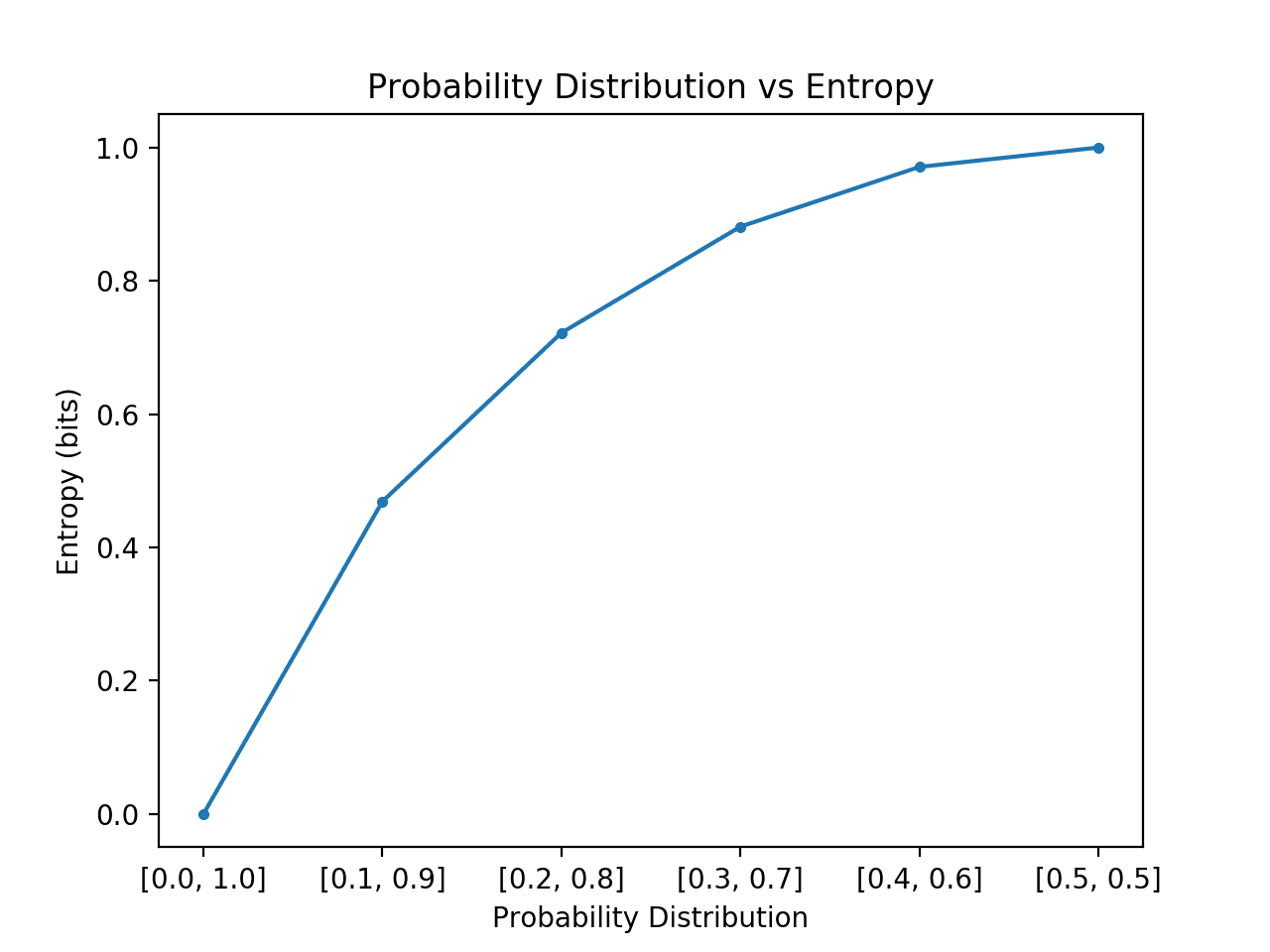
You might recall that information quantifies how surprising an event is in bits. Lower probability events have more information, higher probability events have less information. Entropy quantifies how much information there is in a random variable, or more specifically its probability distribution. A skewed distribution has a low entropy, whereas a distribution where events have equal probability has a larger entropy.
In information theory, we like to describe the “surprise” of an event. Low probability events are more surprising therefore have a larger amount of information. Whereas probability distributions where the events are equally likely are more surprising and have larger entropy.
- Skewed Probability Distribution (unsurprising): Low entropy.
- Balanced Probability Distribution (surprising): High entropy.
For more on the basics of information and entropy, see the tutorial:
Now, let’s consider the entropy of a dataset.
We can think about the entropy of a dataset in terms of the probability distribution of observations in the dataset belonging to one class or another, e.g. two classes in the case of a binary classification dataset.
One interpretation of entropy from information theory is that it specifies the minimum number of bits of information needed to encode the classification of an arbitrary member of S (i.e., a member of S drawn at random with uniform probability).
— Page 58, Machine Learning, 1997.
For example, in a binary classification problem (two classes), we can calculate the entropy of the data sample as follows:
- Entropy = -(p(0) * log(P(0)) + p(1) * log(P(1)))
A dataset with a 50/50 split of samples for the two classes would have a maximum entropy (maximum surprise) of 1 bit, whereas an imbalanced dataset with a split of 10/90 would have a smaller entropy as there would be less surprise for a randomly drawn example from the dataset.
We can demonstrate this with an example of calculating the entropy for this imbalanced dataset in Python. The complete example is listed below.
|
1 2 3 4 5 6 7 8 9 |
# calculate the entropy for a dataset from math import log2 # proportion of examples in each class class0 = 10/100 class1 = 90/100 # calculate entropy entropy = -(class0 * log2(class0) + class1 * log2(class1)) # print the result print('entropy: %.3f bits' % entropy) |
Running the example, we can see that entropy of the dataset for binary classification is less than 1 bit. That is, less than one bit of information is required to encode the class label for an arbitrary example from the dataset.
|
1 |
entropy: 0.469 bits |
In this way, entropy can be used as a calculation of the purity of a dataset, e.g. how balanced the distribution of classes happens to be.
An entropy of 0 bits indicates a dataset containing one class; an entropy of 1 or more bits suggests maximum entropy for a balanced dataset (depending on the number of classes), with values in between indicating levels between these extremes.
Information gain provides a way to use entropy to calculate how a change to the dataset impacts the purity of the dataset, e.g. the distribution of classes. A smaller entropy suggests more purity or less surprise.
… information gain, is simply the expected reduction in entropy caused by partitioning the examples according to this attribute.
— Page 57, Machine Learning, 1997.
For example, we may wish to evaluate the impact on purity by splitting a dataset S by a random variable with a range of values.
This can be calculated as follows:
- IG(S, a) = H(S) – H(S | a)
Where IG(S, a) is the information for the dataset S for the variable a for a random variable, H(S) is the entropy for the dataset before any change (described above) and H(S | a) is the conditional entropy for the dataset given the variable a.
This calculation describes the gain in the dataset S for the variable a. It is the number of bits saved when transforming the dataset.
The conditional entropy can be calculated by splitting the dataset into groups for each observed value of a and calculating the sum of the ratio of examples in each group out of the entire dataset multiplied by the entropy of each group.
- H(S | a) = sum v in a Sa(v)/S * H(Sa(v))
Where Sa(v)/S is the ratio of the number of examples in the dataset with variable a has the value v, and H(Sa(v)) is the entropy of group of samples where variable a has the value v.
This might sound a little confusing.
We can make the calculation of information gain concrete with a worked example.
Want to Learn Probability for Machine Learning
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Worked Example of Calculating Information Gain
In this section, we will make the calculation of information gain concrete with a worked example.
We can define a function to calculate the entropy of a group of samples based on the ratio of samples that belong to class 0 and class 1.
|
1 2 3 |
# calculate the entropy for the split in the dataset def entropy(class0, class1): return -(class0 * log2(class0) + class1 * log2(class1)) |
Now, consider a dataset with 20 examples, 13 for class 0 and 7 for class 1. We can calculate the entropy for this dataset, which will have less than 1 bit.
|
1 2 3 4 5 6 7 |
... # split of the main dataset class0 = 13 / 20 class1 = 7 / 20 # calculate entropy before the change s_entropy = entropy(class0, class1) print('Dataset Entropy: %.3f bits' % s_entropy) |
Now consider that one of the variables in the dataset has two unique values, say “value1” and “value2.” We are interested in calculating the information gain of this variable.
Let’s assume that if we split the dataset by value1, we have a group of eight samples, seven for class 0 and one for class 1. We can then calculate the entropy of this group of samples.
|
1 2 3 4 5 6 7 |
... # split 1 (split via value1) s1_class0 = 7 / 8 s1_class1 = 1 / 8 # calculate the entropy of the first group s1_entropy = entropy(s1_class0, s1_class1) print('Group1 Entropy: %.3f bits' % s1_entropy) |
Now, let’s assume that we split the dataset by value2; we have a group of 12 samples with six in each group. We would expect this group to have an entropy of 1.
|
1 2 3 4 5 6 7 |
... # split 2 (split via value2) s2_class0 = 6 / 12 s2_class1 = 6 / 12 # calculate the entropy of the second group s2_entropy = entropy(s2_class0, s2_class1) print('Group2 Entropy: %.3f bits' % s2_entropy) |
Finally, we can calculate the information gain for this variable based on the groups created for each value of the variable and the calculated entropy.
The first variable resulted in a group of eight examples from the dataset, and the second group had the remaining 12 samples in the data set. Therefore, we have everything we need to calculate the information gain.
In this case, information gain can be calculated as:
- Entropy(Dataset) – (Count(Group1) / Count(Dataset) * Entropy(Group1) + Count(Group2) / Count(Dataset) * Entropy(Group2))
Or:
- Entropy(13/20, 7/20) – (8/20 * Entropy(7/8, 1/8) + 12/20 * Entropy(6/12, 6/12))
Or in code:
|
1 2 3 4 |
... # calculate the information gain gain = s_entropy - (8/20 * s1_entropy + 12/20 * s2_entropy) print('Information Gain: %.3f bits' % gain) |
Tying this all together, the complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
# calculate the information gain from math import log2 # calculate the entropy for the split in the dataset def entropy(class0, class1): return -(class0 * log2(class0) + class1 * log2(class1)) # split of the main dataset class0 = 13 / 20 class1 = 7 / 20 # calculate entropy before the change s_entropy = entropy(class0, class1) print('Dataset Entropy: %.3f bits' % s_entropy) # split 1 (split via value1) s1_class0 = 7 / 8 s1_class1 = 1 / 8 # calculate the entropy of the first group s1_entropy = entropy(s1_class0, s1_class1) print('Group1 Entropy: %.3f bits' % s1_entropy) # split 2 (split via value2) s2_class0 = 6 / 12 s2_class1 = 6 / 12 # calculate the entropy of the second group s2_entropy = entropy(s2_class0, s2_class1) print('Group2 Entropy: %.3f bits' % s2_entropy) # calculate the information gain gain = s_entropy - (8/20 * s1_entropy + 12/20 * s2_entropy) print('Information Gain: %.3f bits' % gain) |
First, the entropy of the dataset is calculated at just under 1 bit. Then the entropy for the first and second groups are calculated at about 0.5 and 1 bits respectively.
Finally, the information gain for the variable is calculated as 0.117 bits. That is, the gain to the dataset by splitting it via the chosen variable is 0.117 bits.
|
1 2 3 4 |
Dataset Entropy: 0.934 bits Group1 Entropy: 0.544 bits Group2 Entropy: 1.000 bits Information Gain: 0.117 bits |
Examples of Information Gain in Machine Learning
Perhaps the most popular use of information gain in machine learning is in decision trees.
An example is the Iterative Dichotomiser 3 algorithm, or ID3 for short, used to construct a decision tree.
Information gain is precisely the measure used by ID3 to select the best attribute at each step in growing the tree.
— Page 58, Machine Learning, 1997.
The information gain is calculated for each variable in the dataset. The variable that has the largest information gain is selected to split the dataset. Generally, a larger gain indicates a smaller entropy or less surprise.
Note that minimizing the entropy is equivalent to maximizing the information gain …
— Page 547, Machine Learning: A Probabilistic Perspective, 2012.
The process is then repeated on each created group, excluding the variable that was already chosen. This stops once a desired depth to the decision tree is reached or no more splits are possible.
The process of selecting a new attribute and partitioning the training examples is now repeated for each non terminal descendant node, this time using only the training examples associated with that node. Attributes that have been incorporated higher in the tree are excluded, so that any given attribute can appear at most once along any path through the tree.
— Page 60, Machine Learning, 1997.
Information gain can be used as a split criterion in most modern implementations of decision trees, such as the implementation of the Classification and Regression Tree (CART) algorithm in the scikit-learn Python machine learning library in the DecisionTreeClassifier class for classification.
This can be achieved by setting the criterion argument to “entropy” when configuring the model; for example:
|
1 2 3 4 |
# example of a decision tree trained with information gain from sklearn.tree import DecisionTreeClassifier model = sklearn.tree.DecisionTreeClassifier(criterion='entropy') ... |
Information gain can also be used for feature selection prior to modeling.
It involves calculating the information gain between the target variable and each input variable in the training dataset. The Weka machine learning workbench provides an implementation of information gain for feature selection via the InfoGainAttributeEval class.
In this context of feature selection, information gain may be referred to as “mutual information” and calculate the statistical dependence between two variables. An example of using information gain (mutual information) for feature selection is the mutual_info_classif() scikit-learn function.
What Is Mutual Information?
Mutual information is calculated between two variables and measures the reduction in uncertainty for one variable given a known value of the other variable.
A quantity called mutual information measures the amount of information one can obtain from one random variable given another.
— Page 310, Data Mining: Practical Machine Learning Tools and Techniques, 4th edition, 2016.
The mutual information between two random variables X and Y can be stated formally as follows:
- I(X ; Y) = H(X) – H(X | Y)
Where I(X ; Y) is the mutual information for X and Y, H(X) is the entropy for X and H(X | Y) is the conditional entropy for X given Y. The result has the units of bits.
Mutual information is a measure of dependence or “mutual dependence” between two random variables. As such, the measure is symmetrical, meaning that I(X ; Y) = I(Y ; X).
It measures the average reduction in uncertainty about x that results from learning the value of y; or vice versa, the average amount of information that x conveys about y.
— Page 139, Information Theory, Inference, and Learning Algorithms, 2003.
Kullback-Leibler, or KL, divergence is a measure that calculates the difference between two probability distributions.
The mutual information can also be calculated as the KL divergence between the joint probability distribution and the product of the marginal probabilities for each variable.
If the variables are not independent, we can gain some idea of whether they are ‘close’ to being independent by considering the Kullback-Leibler divergence between the joint distribution and the product of the marginals […] which is called the mutual information between the variables
— Page 57, Pattern Recognition and Machine Learning, 2006.
This can be stated formally as follows:
- I(X ; Y) = KL(p(X, Y) || p(X) * p(Y))
Mutual information is always larger than or equal to zero, where the larger the value, the greater the relationship between the two variables. If the calculated result is zero, then the variables are independent.
Mutual information is often used as a general form of a correlation coefficient, e.g. a measure of the dependence between random variables.
It is also used as an aspect in some machine learning algorithms. A common example is the Independent Component Analysis, or ICA for short, that provides a projection of statistically independent components of a dataset.
How Are Information Gain and Mutual Information Related?
Mutual Information and Information Gain are the same thing, although the context or usage of the measure often gives rise to the different names.
For example:
- Effect of Transforms to a Dataset (decision trees): Information Gain.
- Dependence Between Variables (feature selection): Mutual Information.
Notice the similarity in the way that the mutual information is calculated and the way that information gain is calculated; they are equivalent:
- I(X ; Y) = H(X) – H(X | Y)
and
- IG(S, a) = H(S) – H(S | a)
As such, mutual information is sometimes used as a synonym for information gain. Technically, they calculate the same quantity if applied to the same data.
We can understand the relationship between the two as the more the difference in the joint and marginal probability distributions (mutual information), the larger the gain in information (information gain).
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Books
- Information Theory, Inference, and Learning Algorithms, 2003.
- Machine Learning: A Probabilistic Perspective, 2012.
- Pattern Recognition and Machine Learning, 2006.
- Machine Learning, 1997.
- Data Mining: Practical Machine Learning Tools and Techniques, 4th edition, 2016.
API
Articles
- Entropy (information theory), Wikipedia.
- Information gain in decision trees, Wikipedia.
- ID3 algorithm, Wikipedia.
- Information gain ratio, Wikipedia.
- Mutual Information, Wikipedia.
Summary
In this post, you discovered information gain and mutual information in machine learning.
Specifically, you learned:
- Information gain is the reduction in entropy or surprise by transforming a dataset and is often used in training decision trees.
- Information gain is calculated by comparing the entropy of the dataset before and after a transformation.
- Mutual information calculates the statistical dependence between two variables and is the name given to information gain when applied to variable selection.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.






Very informative about machine learning
Thanks.
1.can u please provide me any example of how to calculate mutual information.
2.please give me example of how to plot graph of mutual information vs number of parameters and then to estimate number of bits per per parameter.
See the above tutorial for the calculation.
Sorry, I cannot create the plot you’re describing.
mutual information= b+b (p log2p +(1-p) log2(1-p))
p is fraction of correctly classified samples.
b is number of samples
X is (n x b) ,y=(1Xb )
n is dimentionality of input
can u explain how should i implement it by using lstm ??
CAPACITY AND TRAINABILITY IN RECURRENT
NEURAL NETWORKS — 2.1.1 section
How would mutual information be relevant to an LSTM?
Hi,
“A larger entropy suggests lower probability events or more surprise, whereas…”
I think that lower probability events (or more surprise) are related to small entropy, isn’t it?
thank you
No, the relationship is inverted.
See this:
https://machinelearningmastery.com/what-is-information-entropy/
Hello Jason,
Thank you.
This is exactly what I mean: -p*log(p) –> 0 as p->0, so
a smaller entropy = more surprise (e.g. a rainy day in the desert), rather than larger entropy…
sincerely,
HR
Ah yes, my language around this was poor. I was mixing the probability to information relationship with the probability distribution to entropy relationship.
I have updated the intro comments.
Thanks again!
Very well explained. Thank you.
One thing I always wonder is how we can compute an entropy of a dataset if we don’t have its real distribution.
For example, for dataset X = {x_i \in R^D}, how to calculate the H(X) = integrate p(x_i) log p(x_i) d x_i?
Do we use approximation, like sum_j p(bin_j) log p(bin_j)? And, bin_j represents a range of values x_i’s falling into.
Thanks!
Good question, I think this will help:
https://machinelearningmastery.com/what-is-information-entropy/
Hi Jason,
You have explained the article very well, really appreciable !!!
I think, for the below formula, just before the calculation for Group 2, instead of ‘+’, it should be ‘-‘,
Entropy(Dataset) – Count(Group1) / Count(Dataset) * Entropy(Group1) + Count(Group2) / Count(Dataset) * Entropy(Group2)
same for below equation:
Entropy(13/20, 7/20) – 8/20 * Entropy(7/8, 1/8) + 12/20 * Entropy(6/12, 6/12)
Why do you say that exactly?
The subtraction is for the both split1 and split2 gains. So the final “+” needs to be a “-” or place parentheses to group split1 & split2 together.
Thanks David, updated.
Hi,
I have a dataset with huge number of features (~13000) ( all numerical), and number of data points close to 2000, from my analysis it is evident that NOT all the variables contribute to the response, and there is a need for feature selection, but I am having a hard time selecting a feature selection method, could you please suggest me any method for this kind of problem?
Good question, this will help:
https://machinelearningmastery.com/faq/single-faq/what-feature-selection-method-should-i-use
Thanks for your discription, it’s totally helpful.
I have a question that is: In terms of a neural network, how to caculate the mutual information of input ‘x’ and output ‘y’, or ‘x’ and latent representation ‘z’? They have different shapes and we don’t know their distributions, could you please suggest me any information of this problem?
You’re welcome.
I’m not sure off the cuff, sorry. Perhaps experiment.
1- Does high information mean something good, something like getting more information? if yes, how information gain is called “gain” despite it opposite to entropy, more entropy means more surprise, so more information. So. how less information (less entropy) called “information gain”?
2- You said “A smaller entropy suggests more purity or less surprise.” but what I understood that the purity means how balanced is the probability distribution. So, how smaller entropy suggest more purity ? – small entropy should mean more un-balanced distribution! –
Information is neither good nor bad, it is just something we can measure.
“Gain” just means a change in information.
Perhaps this will help in understanding entropy better:
https://machinelearningmastery.com/what-is-information-entropy/
Hi Jason,
Thanks for your great article (as usual) and your reply!
Regarding the second point, I am already read the article and as far as I understood surprising means more information and in case of Balanced/Uniform Probability Distribution, we are more surprising, so more information, more entropy. That contradicts this “A smaller entropy suggests more purity” (if purity means how balanced is the probability distribution.).
Thank you very much for this great explanation!
can I use MI to find the representative feature mean if I had two classes that can be discriminated by a set of features( Of course there will be some feature in common), and I want to say that features 1 and 2 are for class1, and 2,3 for class 2. or is there a simpler way for that.
You’re welcome.
Yes, mutual information can helpful to score feature importance and can be used in filter-based feature selection. I have many examples on the blog you can use as a starting point, use the search box.
I gained a lot of information. Haha.
Thanks!
Hi,
First of all, thank you for this post!
My question is the following:
Can we use Mutual Information when variables are not normally distributed?
Thank you
Have a nice day
I believe so.
HI Jason,
Thank you for the great post. I have been reading the Probabilities for Machine Learning book but I am struggling to understand the relationship between Information Gain and Mutual Information. Specifically, it was stated that the formula for calculating the I(X; Y) and IG(S, a) are equivalent. However, I’m not sure that I fully follow that.
I understood I(X; Y) focuses on the relationship between 2 random variables X and Y, whereas IG(S, a) measures the reduction in entropy by splitting a dataset by random variable a. Therefore, in IG formula, isn’t a part of S? I gave a great example for IG, but if possible, could you help clarify the I(X; Y) formula by given an example which shows IG and I(X; Y) are equivalent?
Thank you!
You’re welcome.
S and a are two “variables” just like X and Y. We perform the same calculation on a split of the data as we do on two columns in a dataset.
Thanks for your helpful post.
I think that it would be better if you mention before the section on mutual information that the information gain and mutual information are the same. it’s not clear when reading what’s the difference between them … (till your note at the end that there isn’t any difference)
Thanks for the suggestion!
My experience is that the mutual information and feature importance from a trained tree-based model will give different results and rankings in terms of important features. So if information gain and mutual information are the same, I am wondering what causes the difference?
Probably some random nature in the training procedure of your tree model?
Thank you very much for the helpful and great explanation, I learned a lot from it since I was practicing the VFDT algorithm these days. But, I got something confused, hope you can answer it :D.
I am struggling with the entropy calculation. In my situation, not all the values in features will match a class (binary class 0,1). So when I was calculating the entropy. There will always be zero-number-class value.
For example,
…
# split 1 (split via value1)
s1_class0 = 8 / 8
s1_class1 = 0 / 8
s1_entropy = entropy(s1_class0, s1_class1)
However, in this case, since s1_class1 = 0, entropy calculation will give NaN since log2(0) cannot be calculated.
…
def entropy(class0, class1):
return -(class0 * log2(class0) + class1 * log2(class1))
Idk whether I am misunderstanding something, but it looks weird.
True. Usually the way is to ignore zero probabilities. In other words, for the equation “p log(p)” where p is zero, we assume it to be zero (0 times NaN = 0)
In the book – Understanding machine learning from theory to algorithms, it says the gain measure can be calculated in various ways like, train error, information gain & gini index. Gini Index is used in CART & information gain is used in ID3 algorithm. What about the train error & is it similar to information gain?
How can we calculate gain using the train error – any post?
Quoting the book:
Implementations of the gain measure:
Train Error: The simplest definition of gain is the decrease in training error.
Formally, let C(a) = min{a, 1−a}. Note that the training error before splitting on
feature i is C(PS[y = 1]), since we took a majority vote among labels. Similarly,
the error after splitting on feature i is
(given formula)
Information Gain: Another popular gain measure that is used in the ID3
and C4.5 algorithms of Quinlan (1993) is the information gain. The information
gain is the difference between the entropy of the label before and after the split,
and is achieved by replacing the function C in the previous expression by the
entropy function,
C(a) = −a log(a) − (1 − a) log(1 − a).
For the error used in training loop, I think this post will help: https://machinelearningmastery.com/cross-entropy-for-machine-learning/
Hello Jason,
I have a dataset with about 20,000 features and I would like to compute the mutual information for lets say feature 1 and 2 . I would be grateful if you can provide some guidance on that.
The aim is to able to do a pairwise feature comparison by looking at the mutual information.
Thanks in advance.
Find the probability distribution (empirical distribution is sufficient) of feature 1, feature 2, and the multivariate distribution of both features 1 and 2. Then you can apply the formula for that.
Hi Jason,
I have a dataset with over 20,0000 features. I would like to do a pairwise comparison of the features . From the tutorial on this page, mutual information is used to select features. My question is how, do I calculate the mutual information between any two features.
You need to find the probability distribution of the features first. Then apply the formula. You may also consider using scikit-learn: https://scikit-learn.org/stable/modules/generated/sklearn.feature_selection.mutual_info_classif.html
Hello,
I want to compute the attribute weight for the categorical feature in the regression problem.
Something similar to attribute-weighted value difference metric for regression tasks.
can you give me any suggestions?
Hi Nal…I would recommend reviewing the various regression metrics for regression applications:
https://machinelearningmastery.com/regression-metrics-for-machine-learning/
What’s the relationship between using this approach vs using conventional Lasso / Ridge Regression for variable selection?
Hi Eugene…the following may be of interest to you:
https://machinelearningmastery.com/lasso-regression-with-python/
Hello, Article is very informative. I would like to know in the case of multiclass datasets, do we still consider log2 or logn while calculating entropy (n represents the number of classes)?
Hi Aparna…the following resource may help clarify:
https://gombru.github.io/2018/05/23/cross_entropy_loss/
Hi Jason,
Thanks for the article it is really interesting and useful !
I have 2 questions :
1) Are there rules of thumbs to decide the right percentage of features to keep during feature selection ? Is is 10%, 20%, 30%, more ?
2) I read somewhere that mutual information is a positive number that has no bound.
However, It is rare to have a mutual information greater than 2.
Knowing that, is there a threshold for mutual information beyond which the feature is most likely relevant to predict the target variable ?
Thanks !
In which book of yours is Imformation Gain explained?
Hi Omkar…The following resource provides content related to this topic:
https://machinelearningmastery.com/probability-for-machine-learning/
Hi, thanks for this great explanation!
Does mutual_info_score of the scikit-learn do the same job?
Hi Shayan…The following reference may add clarity:
https://scikit-learn.org/stable/modules/generated/sklearn.metrics.mutual_info_score.html
In section What is information gain? 4th paragraph “In information theory, we like to describe the “surprise” of an event. Low probability events are more surprising therefore have a larger amount of information.”
isn’t this supposed to be low probability events are “less surprising”…?
Hi Sahil…You are correct. The term was used to indicate a relative comparison that could be measured based upon probability values. In other words, it was used just a term to attach the scoring of events.
Great great explanation and makes me more interested in the topic. The logic chain is so clear and the best for beginners.
Thank you for your feedback Alicia! We appreciate it!