Last Updated on August 7, 2019
Attention is a mechanism that was developed to improve the performance of the Encoder-Decoder RNN on machine translation.
In this tutorial, you will discover the attention mechanism for the Encoder-Decoder model.
After completing this tutorial, you will know:
- About the Encoder-Decoder model and attention mechanism for machine translation.
- How to implement the attention mechanism step-by-step.
- Applications and extensions to the attention mechanism.
Kick-start your project with my new book Deep Learning for Natural Language Processing, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
- Update Dec/2017: Fixed a small typo in Step 4, thanks Cynthia Freeman.
Tutorial Overview
This tutorial is divided into 4 parts; they are:
- Encoder-Decoder Model
- Attention Model
- Worked Example of Attention
- Extensions to Attention
Encoder-Decoder Model
The Encoder-Decoder model for recurrent neural networks was introduced in two papers.
Both developed the technique to address the sequence-to-sequence nature of machine translation where input sequences differ in length from output sequences.
Ilya Sutskever, et al. do so in the paper “Sequence to Sequence Learning with Neural Networks” using LSTMs.
Kyunghyun Cho, et al. do so in the paper “Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation“. This work, and some of the same authors (Bahdanau, Cho and Bengio) developed their specific model later to develop an attention model. Therefore we will take a quick look at the Encoder-Decoder model as described in this paper.
From a high-level, the model is comprised of two sub-models: an encoder and a decoder.
- Encoder: The encoder is responsible for stepping through the input time steps and encoding the entire sequence into a fixed length vector called a context vector.
- Decoder: The decoder is responsible for stepping through the output time steps while reading from the context vector.
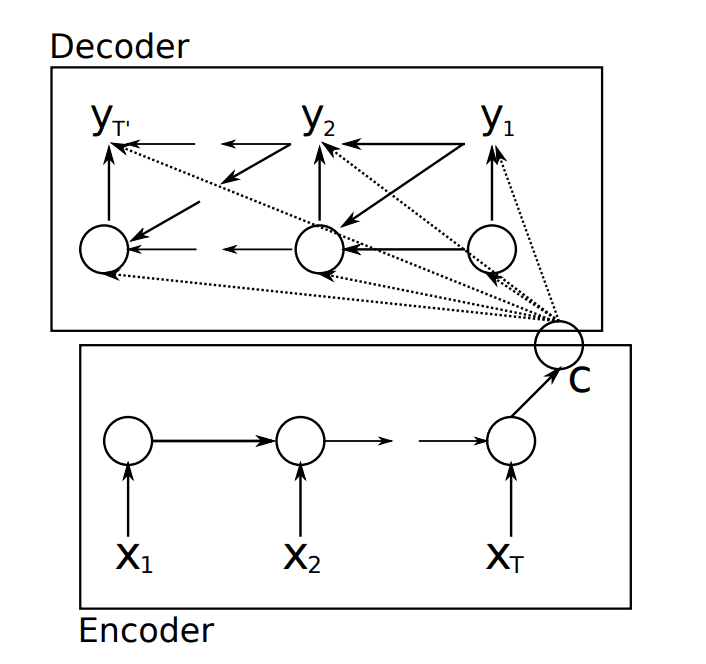
Encoder-Decoder Recurrent Neural Network Model.
Taken from “Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation”
we propose a novel neural network architecture that learns to encode a variable-length sequence into a fixed-length vector representation and to decode a given fixed-length vector representation back into a variable-length sequence.
— Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation, 2014.
Key to the model is that the entire model, including encoder and decoder, is trained end-to-end, as opposed to training the elements separately.
The model is described generically such that different specific RNN models could be used as the encoder and decoder.
Instead of using the popular Long Short-Term Memory (LSTM) RNN, the authors develop and use their own simple type of RNN, later called the Gated Recurrent Unit, or GRU.
Further, unlike the Sutskever, et al. model, the output of the decoder from the previous time step is fed as an input to decoding the next output time step. You can see this in the image above where the output y2 uses the context vector (C), the hidden state passed from decoding y1 as well as the output y1.
… both y(t) and h(i) are also conditioned on y(t−1) and on the summary c of the input sequence.
— Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation, 2014
Attention Model
Attention was presented by Dzmitry Bahdanau, et al. in their paper “Neural Machine Translation by Jointly Learning to Align and Translate” that reads as a natural extension of their previous work on the Encoder-Decoder model.
Attention is proposed as a solution to the limitation of the Encoder-Decoder model encoding the input sequence to one fixed length vector from which to decode each output time step. This issue is believed to be more of a problem when decoding long sequences.
A potential issue with this encoder–decoder approach is that a neural network needs to be able to compress all the necessary information of a source sentence into a fixed-length vector. This may make it difficult for the neural network to cope with long sentences, especially those that are longer than the sentences in the training corpus.
— Neural Machine Translation by Jointly Learning to Align and Translate, 2015.
Attention is proposed as a method to both align and translate.
Alignment is the problem in machine translation that identifies which parts of the input sequence are relevant to each word in the output, whereas translation is the process of using the relevant information to select the appropriate output.
… we introduce an extension to the encoder–decoder model which learns to align and translate jointly. Each time the proposed model generates a word in a translation, it (soft-)searches for a set of positions in a source sentence where the most relevant information is concentrated. The model then predicts a target word based on the context vectors associated with these source positions and all the previous generated target words.
— Neural Machine Translation by Jointly Learning to Align and Translate, 2015.
Instead of encoding the input sequence into a single fixed context vector, the attention model develops a context vector that is filtered specifically for each output time step.
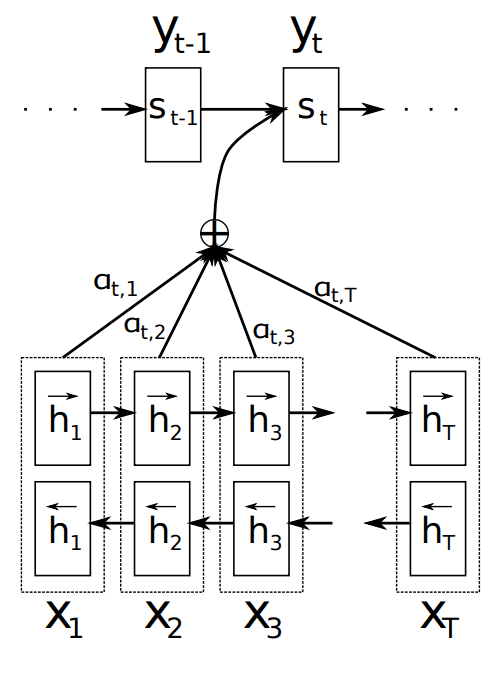
Example of Attention
Taken from “Neural Machine Translation by Jointly Learning to Align and Translate”, 2015.
As with the Encoder-Decoder paper, the technique is applied to a machine translation problem and uses GRU units rather than LSTM memory cells. In this case, a bidirectional input is used where the input sequences are provided both forward and backward, which are then concatenated before being passed on to the decoder.
Rather than re-iterate the equations for calculating attention, we will look at a worked example.
Need help with Deep Learning for Text Data?
Take my free 7-day email crash course now (with code).
Click to sign-up and also get a free PDF Ebook version of the course.
Worked Example of Attention
In this section, we will make attention concrete with a small worked example. Specifically, we will step through the calculations with un-vectorized terms.
This will give you a sufficiently detailed understanding that you could add attention to your own encoder-decoder implementation.
This worked example is divided into the following 6 sections:
- Problem
- Encoding
- Alignment
- Weighting
- Context Vector
- Decode
1. Problem
The problem is a simple sequence-to-sequence prediction problem.
There are three input time steps:
|
1 |
x1, x2, x3 |
The model is required to predict 1 time step:
|
1 |
y1 |
In this example, we will ignore the type of RNN being used in the encoder and decoder and ignore the use of a bidirectional input layer. These elements are not salient to understanding the calculation of attention in the decoder.
2. Encoding
In the encoder-decoder model, the input would be encoded as a single fixed-length vector. This is the output of the encoder model for the last time step.
|
1 |
h1 = Encoder(x1, x2, x3) |
The attention model requires access to the output from the encoder for each input time step. The paper refers to these as “annotations” for each time step. In this case:
|
1 |
h1, h2, h3 = Encoder(x1, x2, x3) |
3. Alignment
The decoder outputs one value at a time, which is passed on to perhaps more layers before finally outputting a prediction (y) for the current output time step.
The alignment model scores (e) how well each encoded input (h) matches the current output of the decoder (s).
The calculation of the score requires the output from the decoder from the previous output time step, e.g. s(t-1). When scoring the very first output for the decoder, this will be 0.
Scoring is performed using a function a(). We can score each annotation (h) for the first output time step as follows:
|
1 2 3 |
e11 = a(0, h1) e12 = a(0, h2) e13 = a(0, h3) |
We use two subscripts for these scores, e.g. e11 where the first “1” represents the output time step, and the second “1” represents the input time step.
We can imagine that if we had a sequence-to-sequence problem with two output time steps, that later we could score the annotations for the second time step as follows (assuming we had already calculated our s1):
|
1 2 3 |
e21 = a(s1, h1) e22 = a(s1, h2) e23 = a(s1, h3) |
The function a() is called the alignment model in the paper and is implemented as a feedforward neural network.
This is a traditional one layer network where each input (s(t-1) and h1, h2, and h3) is weighted, a hyperbolic tangent (tanh) transfer function is used and the output is also weighted.
4. Weighting
Next, the alignment scores are normalized using a softmax function.
The normalization of the scores allows them to be treated like probabilities, indicating the likelihood of each encoded input time step (annotation) being relevant to the current output time step.
These normalized scores are called annotation weights.
For example, we can calculate the softmax annotation weights (a) given the calculated alignment scores (e) as follows:
|
1 2 3 |
a11 = exp(e11) / (exp(e11) + exp(e12) + exp(e13)) a12 = exp(e12) / (exp(e11) + exp(e12) + exp(e13)) a13 = exp(e13) / (exp(e11) + exp(e12) + exp(e13)) |
If we had two output time steps, the annotation weights for the second output time step would be calculated as follows:
|
1 2 3 |
a21 = exp(e21) / (exp(e21) + exp(e22) + exp(e23)) a22 = exp(e22) / (exp(e21) + exp(e22) + exp(e23)) a23 = exp(e23) / (exp(e21) + exp(e22) + exp(e23)) |
5. Context Vector
Next, each annotation (h) is multiplied by the annotation weights (a) to produce a new attended context vector from which the current output time step can be decoded.
We only have one output time step for simplicity, so we can calculate the single element context vector as follows (with brackets for readability):
|
1 |
c1 = (a11 * h1) + (a12 * h2) + (a13 * h3) |
The context vector is a weighted sum of the annotations and normalized alignment scores.
If we had two output time steps, the context vector would be comprised of two elements [c1, c2], calculated as follows:
|
1 2 |
c1 = a11 * h1 + a12 * h2 + a13 * h3 c2 = a21 * h1 + a22 * h2 + a23 * h3 |
6. Decode
Decoding is then performed as per the Encoder-Decoder model, although in this case using the attended context vector for the current time step.
The output of the decoder (s) is referred to as a hidden state in the paper.
|
1 |
s1 = Decoder(c1) |
This may be fed into additional layers before ultimately exiting the model as a prediction (y1) for the time step.
Extensions to Attention
This section looks at some additional applications of the Bahdanau, et al. attention mechanism.
Hard and Soft Attention
In the 2015 paper “Show, Attend and Tell: Neural Image Caption Generation with Visual Attention“, Kelvin Xu, et al. applied attention to image data using convolutional neural nets as feature extractors for image data on the problem of captioning photos.
They develop two attention mechanisms, one they call “soft attention,” which resembles attention as described above with a weighted context vector, and the second “hard attention” where the crisp decisions are made about elements in the context vector for each word.
They also propose double attention where attention is focused on specific parts of the image.
Dropping the Previous Hidden State
There have been some applications of the mechanism where the approach was simplified so that the hidden state from the last output time step (s(t-1)) is dropped from the scoring of annotations (Step 3. above).
Two examples are:
- Hierarchical Attention Networks for Document Classification, 2016.
- Attention-Based Bidirectional Long Short-Term Memory Networks for Relation Classification, 2016
This has the effect of not providing the model with an idea of the previously decoded output, which is intended to aid in alignment.
This is noted in the equations listed in the papers, and it is not clear if the mission was an intentional change to the model or merely an omission from the equations. No discussion of dropping the term was seen in either paper.
Study the Previous Hidden State
Minh-Thang Luong, et al. in their 2015 paper “Effective Approaches to Attention-based Neural Machine Translation” explicitly restructure the use of the previous decoder hidden state in the scoring of annotations. Also, see the presentation of the paper and associated Matlab code.
They developed a framework to contrast the different ways to score annotations. Their framework calls out and explicitly excludes the previous hidden state in the scoring of annotations.
Instead, they take the previous attentional context vector and pass it as an input to the decoder. The intention is to allow the decoder to be aware of past alignment decisions.
… we propose an input-feeding approach in which attentional vectors ht are concatenated with inputs at the next time steps […]. The effects of having such connections are two-fold: (a) we hope to make the model fully aware of previous alignment choices and (b) we create a very deep network spanning both horizontally and vertically
— Effective Approaches to Attention-based Neural Machine Translation, 2015.
Below is a picture of this approach taken from the paper. Note the dotted lines explictly showing the use of the decoders attended hidden state output (ht) providing input to the decoder on the next timestep.
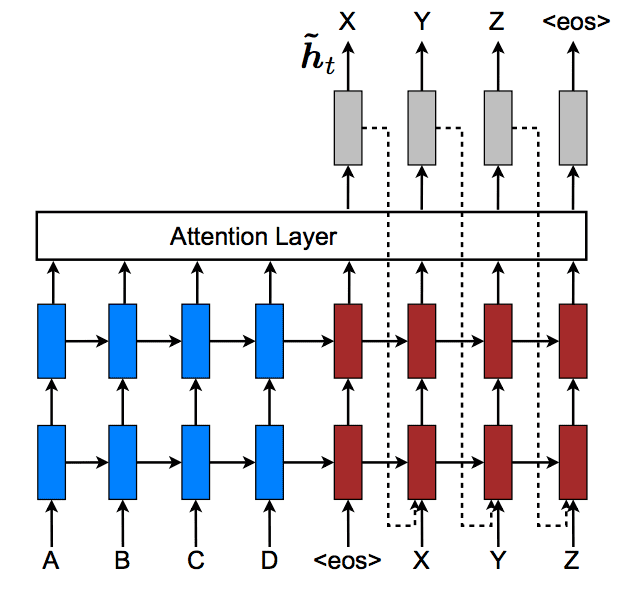
Feeding Hidden State as Input to Decoder
Taken from “Effective Approaches to Attention-based Neural Machine Translation”, 2015.
They also develop “global” vs “local” attention, where local attention is a modification of the approach that learns a fixed-sized window to impose over the attentional vector for each output time step. It is seen as a simpler approach to the “hard attention” presented by Xu, et al.
The global attention has a drawback that it has to attend to all words on the source side for each target word, which is expensive and can potentially render it impractical to translate longer sequences, e.g., paragraphs or documents. To address this deficiency, we propose a local attentional mechanism that chooses to focus only on a small subset of the source positions per target word.
— Effective Approaches to Attention-based Neural Machine Translation, 2015.
Analysis in the paper of global and local attention with different annotation scoring functions suggests that local attention provides better results on the translation task.
Further Reading
This section provides more resources on the topic if you are looking go deeper.
Encoder-Decoder Papers
- Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation, 2014.
- Sequence to Sequence Learning with Neural Networks, 2014.
Attention Papers
- Neural Machine Translation by Jointly Learning to Align and Translate, 2015.
- Show, Attend and Tell: Neural Image Caption Generation with Visual Attention, 2015.
- Hierarchical Attention Networks for Document Classification, 2016.
- Attention-Based Bidirectional Long Short-Term Memory Networks for Relation Classification, 2016
- Effective Approaches to Attention-based Neural Machine Translation, 2015.
More on Attention
- Attention in Long Short-Term Memory Recurrent Neural Networks
- Lecture 10: Neural Machine Translation and Models with Attention, Stanford, 2017
- Lecture 8 – Generating Language with Attention, Oxford.
Summary
In this tutorial, you discovered the attention mechanism for Encoder-Decoder model.
Specifically, you learned:
- About the Encoder-Decoder model and attention mechanism for machine translation.
- How to implement the attention mechanism step-by-step.
- Applications and extensions to the attention mechanism.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
Develop Deep Learning models for Text Data Today!
Develop Your Own Text models in Minutes
...with just a few lines of python code
Discover how in my new Ebook:
Deep Learning for Natural Language Processing
It provides self-study tutorials on topics like:
Bag-of-Words, Word Embedding, Language Models, Caption Generation, Text Translation and much more...
Finally Bring Deep Learning to your Natural Language Processing Projects
Skip the Academics. Just Results.
Hello sir, thanks for the great tutorial. I didn’t get the part how the context vector is practically used in the model. Shall we concatenate the state vector s_t with c_t ([s_t;c_t]) or replace s_t with c_t after calculating it.
Great question.
It is often used as the initial state for the decoder.
Alternately, it could be used as input to the decoder or input to something down stream of the decoder as you describe.
Hi,
I have been struggling with the problem of attention in machine translation.
If the context vector is passed as initial state to the decoder, won’t that be propagated through all the time steps. How will it take a new context vector at every time step?
Also, the initial state needs both hidden state and cell state(context vector). If I initialize the decoder state, what should be given in place of the hidden state?
If I give the context vector as an input to the decoder LSTM, there are shape issues.
Please assist.
Hello,
I’m new to this field, and I did an excellent course by Andrew Ng on Sequence Models on Coursera. In his implementation of the attention model in an assignment, the context vector is actually provided as an input into the decoder LSTM, and not as an initial state.
A sample code is as follows (uses Keras):
decoder_LSTM_cell = LSTM(128, return_state = True)
context = output_of_attention
s, _, c = decoder_LSTM_cell(context, initial_state = [s,c])
Where s and c are the hidden state and cell state at each time step of the decoder LSTM.
Thank you very much, Jason.
But I have a question that if the context vector Ci is the initial_state of Decoder at time step i, what is the initial cell state for it? What I understand is that we need to give both hidden state and cell state for LSTM cell.Thanks!
Great tutorial.
In the worked example you say “There are three input time steps”. Why are there three? Is it three just because of the way you’ve decided to set up the problem? Or, is it three because there are, by definition, always three time time steps in an Encoder Decoder with Attention? Maybe there are three time steps because you have decide to set up the problem such that there are three tokens(words) in the input? (I have a feeling this question shows great ignorance. Should I be reading a more basic tutorial first?
It is arbitrary, it is just as an example.
Just for the sake of correctness, I think you meant in step 4: a13 and a23 instead of a12 and a22 twice
Thanks Cynthia, fixed!
Hi Jason,
It’s a great articles!!
I have a question, in the alignment part, e is the score to tell how well h1, h2… match the current “s” and then continue to calculate the weights and form the context vector. Finally we decode the context vector to get “s”. What are the differences between the first “s” and second “s”? All the score and weight are derived from the first “s” and then we use these values to get “s”? It seems weird to me… Am I understanding right? Thank you!
Hello,
From what I understand, ‘s’ happens to be the hidden state output of the decoder LSTM, and you’re not considering the LSTM layer and the difference in time steps, that lies in between the context vectors and the hidden outputs ‘s’.
The context vector at a particular time step is generated with the help of both the output (‘s’) of the previous time step of the decoder LSTM, and also the hidden state outputs of the encoder LSTM.
So in your question, the first ‘s’ is actually the output of the previous time step of the decoder LSTM, which is used to generate the context vector of the current time step, and this is then passed to the decoder LSTM as input for the current time step, and this generates the second ‘s’ in your question. This ‘s’ will then be used for the next time step and so on.
Hi Jason, thank you for the article!
I’ve been trying to find an answer to this question across the web and couldn’t so far – everybody is quiet about it.
Because the Alignment model a( ) contains a matrix inside of it, does this mean our LSTM is restricted to a fixed number of timesteps? In other words, my English-to-French translation must contain, say, exactly, 10 english words to be translated into, say, exactly 12 French words?
It seems important to impose this restriction since LSTM must learn weights to the input states, and hence the number of timesteps must never change – am I right?
Then it would drastically negate most of RNN’s benefit
Yes.
No, you can work with long sequences, say paragraphs at a time.
Hi Jason,
I recently read a paper in which the attention mechanism of LSTM neural networks was used for Time Series Prediction:
https://arxiv.org/abs/1704.02971
I was thinking of applying it to the Beijing pollution dataset, to see if it can perform better than the classic LSTM that your propose in one of your tutorial.
I would like to know what do you think and if you know if there already some implementation of it in Time Series Prediction or any useful material i can use/read.
Thanks a lot ,
Marco
Thanks for the link to the paper. I’ll read it.
I don’t know if there is an implementation, perhaps you can contact the authors and see if they are willing to share their code?
The font size is too small. But, very nice content! Thank you for that.
Thanks Fred.
hey Jason I want to clear my small doubt regarding the context vector ‘c’ i.e. what will be the desired output of a context vector … ? will it be a number only or an array of vector?
A vector.
can you give me an example please . 🙂
For the line “Instead of decoding the input sequence into a single fixed context vector…” should it be “Instead of encoding the input sequence… “?
Yes, typo. Thanks, fixed.
Hmm i am maybe a bit dumb but i dont get this stuff – why is this so complex :-/
A thing i had a ín my mind for ocr some while ago – cant we just do this:
Translate the label (a word or setence) into a fix size vector – where each character get a specific number /index (like a dictionary)
Now just do the training and tell the cnn to map my input features/activations – to the label vector – which represents my word he should detect. Thats all.
Does this makes any sense at all and is this realistic?
Would i need a custom loss function?
Thank you for any comments on this.
In your case, perhaps attention is not required, it sounds like a straight image classification task.
Actually you are right! Thank you for your answer and helping me rethink 🙂
No problem.
How can the attention models be used to generate text (sequence of characters) from a handwritten image?
(Handwriting recognition and generation of the corresponding text).
Sorry, I don’t have an example of this.
Hi, sir. How the decoder knows when to end? I mean, when translating a sentence how do we know how many words should be in the target sentence?
You can decide to stop calling it or it can output a “end of sequence” token.
Yes, but how does decoder “know” when to end? It is the result of training? that means decoder treats EOS as a normal word, right?
It learns how long sequences are and when to end them.
This applies to encoder-decoder type models, such as the language model in the caption generator as a example:
https://machinelearningmastery.com/develop-a-deep-learning-caption-generation-model-in-python/
“The function a() is called the alignment model in the paper and is implemented as a feedforward neural network.” – one question regarding this function a(.):
What target values it use? I mean if a(.) is “a traditional one layer network where each input (s(t-1) and h1, h2, and h3) is weighted, a hyperbolic tangent (tanh) transfer function is used and the output is also weighted”, then what are the target_values for this network?
Thank you in advance, I couldn’t find the answer by googling.
Another Excellent tutorial by Jason. Hey Jason, it was the most clear explanation of encoder-decoders on the whole internet. I just wanted to make a request. Can You please make a tutorial on how to use: tf.keras.layers.AdditiveAttention layer. As Keras is easy to implement and understand, using Attention layer in it would also be easy. So, I request you Jason to please make a tutorial on this.
Thanks in advance!
Sorry, I meant the most clear explanation of attention in encoder-decoders on the whole internet
Thanks.
Yes, I hope to write new tutorials on this topic soon.
Hello, Jason. The attention which you taught to implement in this tutorial, was that Bahdanau attention or which attention?
Yes.
Can you please make a tutorial on how to implement the things described here, as I am just getting started with machine Learning.
Yes.
Hello Jason,
a21 = exp(e21) / (exp(e21) + exp(e22) + exp(e23))
What does exp mean here?
It is a specification of one aspect of the attention layer described in the paper.
CAN YOU PLEASE MAKE A TUTORIAL ON IMPLEMENTING THESE THINGS IN KERAS ON AN NLP TASK
Thanks for the suggestion.
Hello Jason, I tested my first Bahdanau attention model on Machine Language Translation problem. But, unfortunately, the model without attention mechanism performed better than the one with attention. What could be the reason to this?
Perhaps attention is a bad fit for your model.
Perhaps your model with attention requires tuning.
Perhaps an alternate type of attention is required.
…
Do you have a working example with code for Encoder – Decoder RNNs with attention? If so, could you give me the link?
Not at this stage.
How a Transformer Network is different from an Encoder – Decoder RNNs with attention layer.
Thank you.
Sorry, I don’t have tutorials on the transformer. I hope to write about the topic in the future.
One of your best articles!
Thank you! Hope you enjoyed it.
Hi. I am confused that when the context vector is being calculated, they say the last hidden state of decoder is used, but when I look at the sample codes, all hidden states of the decoder until time step t-1 are used in the attention layer. Which one is correct? Thanks.
Attention should include all time steps.