Do Not Use Random Guessing As Your Baseline Classifier

I recently received the following question via email:

Hi Jason, quick question. A case of class imbalance: 90 cases of thumbs up 10 cases of thumbs down. How would we calculate random guessing accuracy in this case?

We can answer this question using some basic probability (I opened excel and typed in some numbers).

Kick-start your project with my new book Probability for Machine Learning, including step-by-step tutorials and the Python source code files for all examples.

Let’s get started.

Note, for a more detailed tutorial on this topic, see:

• How to Develop and Evaluate Naive Classifier Strategies Using Probability

Don’t Use Random Guessing As Your Baseline Classifier
Photo by cbgrfx123, some rights reserved.

Let’s say the split is 90%-10% for class 0 and class 1. Let’s also say that you will guess randomly using the same ratio.

The theoretical accuracy of random guessing on a two-classification problem is:

We can test this on our example 90%-10% split:

To check the math, you can plug-in a 50%-50% split of your data and it matches your intuition:

If we look on Google, we find a similar question on Cross Validated “What is the chance level accuracy in unbalanced classification problems?” with an almost identical answer. Again, a nice confirmation.

Interesting, but there is an important takeaway point from all of this.

Don’t Use Random Guessing As A Baseline

If you are looking for a classifier to use as a baseline accuracy, don’t use random guessing.

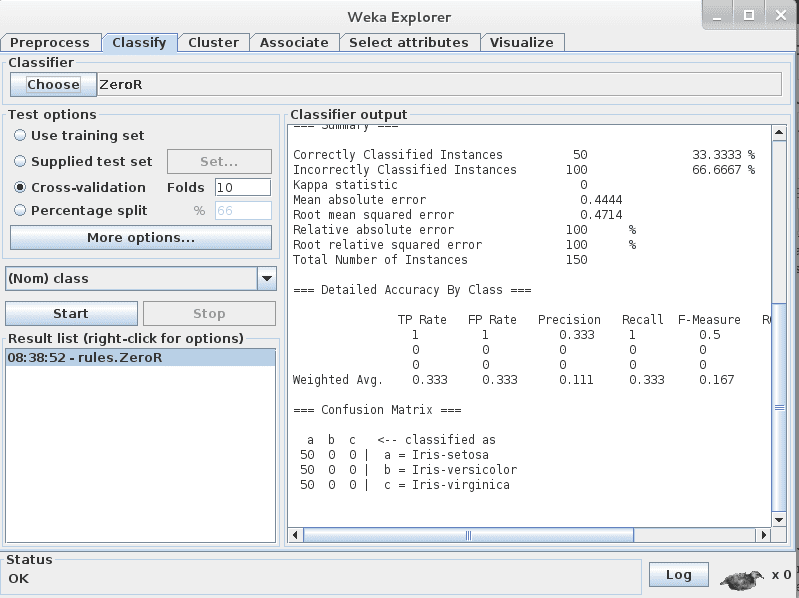
There is a classifier called Zero Rule (or 0R or ZeroR for short). It is the simplest rule you can use on a classification problem and it simply predicts the majority class in your dataset (e.g. the mode).

In the example above with a 90%-10% for class 0 and class 1 it would predict class 0 for every prediction and achieve an accuracy of 90%. This is 8% better than the theoretical maximum using random guessing.

Use the Zero Rule method as a baseline.

Also, in imbalanced classification problems like this, you should use metrics other than Accuracy such as Kappa or Area under ROC Curve.

For more information about alternative performance measures on classification problems see the post:

• Classification Accuracy is Not Enough: More Performance Measures You Can Use

For more on working with imbalanced classification problems see the post:

• 8 Tactics to Combat Imbalanced Classes in Your Machine Learning Dataset

Do you have any questions about this post? Ask in the comments.

Get a Handle on Probability for Machine Learning!

Develop Your Understanding of Probability

...with just a few lines of python code

Discover how in my new Ebook:
Probability for Machine Learning

It provides self-study tutorials and end-to-end projects on:
Bayes Theorem, Bayesian Optimization, Distributions, Maximum Likelihood, Cross-Entropy, Calibrating Models
and much more...

Finally Harness Uncertainty in Your Projects

Skip the Academics. Just Results.

See What's Inside