Training deep neural networks with tens of layers is challenging as they can be sensitive to the initial random weights and configuration of the learning algorithm.
One possible reason for this difficulty is the distribution of the inputs to layers deep in the network may change after each mini-batch when the weights are updated. This can cause the learning algorithm to forever chase a moving target. This change in the distribution of inputs to layers in the network is referred to the technical name “internal covariate shift.”
Batch normalization is a technique for training very deep neural networks that standardizes the inputs to a layer for each mini-batch. This has the effect of stabilizing the learning process and dramatically reducing the number of training epochs required to train deep networks.
In this post, you will discover the batch normalization method used to accelerate the training of deep learning neural networks.
After reading this post, you will know:
- Deep neural networks are challenging to train, not least because the input from prior layers can change after weight updates.
- Batch normalization is a technique to standardize the inputs to a network, applied to ether the activations of a prior layer or inputs directly.
- Batch normalization accelerates training, in some cases by halving the epochs or better, and provides some regularization, reducing generalization error.
Kick-start your project with my new book Better Deep Learning, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.

A Gentle Introduction to Batch Normalization for Deep Neural Networks
Photo by Dennis Jarvis, some rights reserved.
Overview
This tutorial is divided into five parts; they are:
- Problem of Training Deep Networks
- Standardize Layer Inputs
- How to Standardize Layer Inputs
- Examples of Using Batch Normalization
- Tips for Using Batch Normalization
Problem of Training Deep Networks
Training deep neural networks, e.g. networks with tens of hidden layers, is challenging.
One aspect of this challenge is that the model is updated layer-by-layer backward from the output to the input using an estimate of error that assumes the weights in the layers prior to the current layer are fixed.
Very deep models involve the composition of several functions or layers. The gradient tells how to update each parameter, under the assumption that the other layers do not change. In practice, we update all of the layers simultaneously.
— Page 317, Deep Learning, 2016.
Because all layers are changed during an update, the update procedure is forever chasing a moving target.
For example, the weights of a layer are updated given an expectation that the prior layer outputs values with a given distribution. This distribution is likely changed after the weights of the prior layer are updated.
Training Deep Neural Networks is complicated by the fact that the distribution of each layer’s inputs changes during training, as the parameters of the previous layers change. This slows down the training by requiring lower learning rates and careful parameter initialization, and makes it notoriously hard to train models with saturating nonlinearities.
— Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift, 2015.
The authors of the paper introducing batch normalization refer to change in the distribution of inputs during training as “internal covariate shift.”
We refer to the change in the distributions of internal nodes of a deep network, in the course of training, as Internal Covariate Shift.
— Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift, 2015.
Want Better Results with Deep Learning?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Standardize Layer Inputs
Batch normalization, or batchnorm for short, is proposed as a technique to help coordinate the update of multiple layers in the model.
Batch normalization provides an elegant way of reparametrizing almost any deep network. The reparametrization significantly reduces the problem of coordinating updates across many layers.
— Page 318, Deep Learning, 2016.
It does this scaling the output of the layer, specifically by standardizing the activations of each input variable per mini-batch, such as the activations of a node from the previous layer. Recall that standardization refers to rescaling data to have a mean of zero and a standard deviation of one, e.g. a standard Gaussian.
Batch normalization reparametrizes the model to make some units always be standardized by definition
— Page 319, Deep Learning, 2016.
This process is also called “whitening” when applied to images in computer vision.
By whitening the inputs to each layer, we would take a step towards achieving the fixed distributions of inputs that would remove the ill effects of the internal covariate shift.
— Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift, 2015.
Standardizing the activations of the prior layer means that assumptions the subsequent layer makes about the spread and distribution of inputs during the weight update will not change, at least not dramatically. This has the effect of stabilizing and speeding-up the training process of deep neural networks.
Batch normalization acts to standardize only the mean and variance of each unit in order to stabilize learning, but allows the relationships between units and the nonlinear statistics of a single unit to change.
— Page 320, Deep Learning, 2016.
Normalizing the inputs to the layer has an effect on the training of the model, dramatically reducing the number of epochs required. It can also have a regularizing effect, reducing generalization error much like the use of activation regularization.
Batch normalization can have a dramatic effect on optimization performance, especially for convolutional networks and networks with sigmoidal nonlinearities.
— Page 425, Deep Learning, 2016.
Although reducing “internal covariate shift” was a motivation in the development of the method, there is some suggestion that instead batch normalization is effective because it smooths and, in turn, simplifies the optimization function that is being solved when training the network.
… BatchNorm impacts network training in a fundamental way: it makes the landscape of the corresponding optimization problem be significantly more smooth. This ensures, in particular, that the gradients are more predictive and thus allow for use of larger range of learning rates and faster network convergence.
— How Does Batch Normalization Help Optimization? (No, It Is Not About Internal Covariate Shift), 2018.
How to Standardize Layer Inputs
Batch normalization can be implemented during training by calculating the mean and standard deviation of each input variable to a layer per mini-batch and using these statistics to perform the standardization.
Alternately, a running average of mean and standard deviation can be maintained across mini-batches, but may result in unstable training.
It is natural to ask whether we could simply use the moving averages […] to perform the normalization during training […]. This, however, has been observed to lead to the model blowing up.
— Batch Renormalization: Towards Reducing Minibatch Dependence in Batch-Normalized Models, 2017.
After training, the mean and standard deviation of inputs for the layer can be set as mean values observed over the training dataset.
For small mini-batch sizes or mini-batches that do not contain a representative distribution of examples from the training dataset, the differences in the standardized inputs between training and inference (using the model after training) can result in noticeable differences in performance. This can be addressed with a modification of the method called Batch Renormalization (or BatchRenorm for short) that makes the estimates of the variable mean and standard deviation more stable across mini-batches.
Batch Renormalization extends batchnorm with a per-dimension correction to ensure that the activations match between the training and inference networks.
— Batch Renormalization: Towards Reducing Minibatch Dependence in Batch-Normalized Models, 2017.
This standardization of inputs may be applied to input variables for the first hidden layer or to the activations from a hidden layer for deeper layers.
In practice, it is common to allow the layer to learn two new parameters, namely a new mean and standard deviation, Beta and Gamma respectively, that allow the automatic scaling and shifting of the standardized layer inputs. These parameters are learned by the model as part of the training process.
Note that simply normalizing each input of a layer may change what the layer can represent. […] These parameters are learned along with the original model parameters, and restore the representation power of the network.
— Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift, 2015.
Importantly the backpropagation algorithm is updated to operate upon the transformed inputs, and error is also used to update the new scale and shifting parameters learned by the model.
The standardization is applied to the inputs to the layer, namely the input variables or the output of the activation function from the prior layer. Given the choice of activation function, the distribution of the inputs to the layer may be quite non-Gaussian. In this case, there may be benefit in standardizing the summed activation before the activation function in the previous layer.
We add the BN transform immediately before the nonlinearity […] We could have also normalized the layer inputs u, but since u is likely the output of another nonlinearity, the shape of its distribution is likely to change during training, and constraining its first and second moments would not eliminate the covariate shift.
— Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift, 2015.
Examples of Using Batch Normalization
This section provides a few examples of milestone papers and popular models that make use of batch normalization.
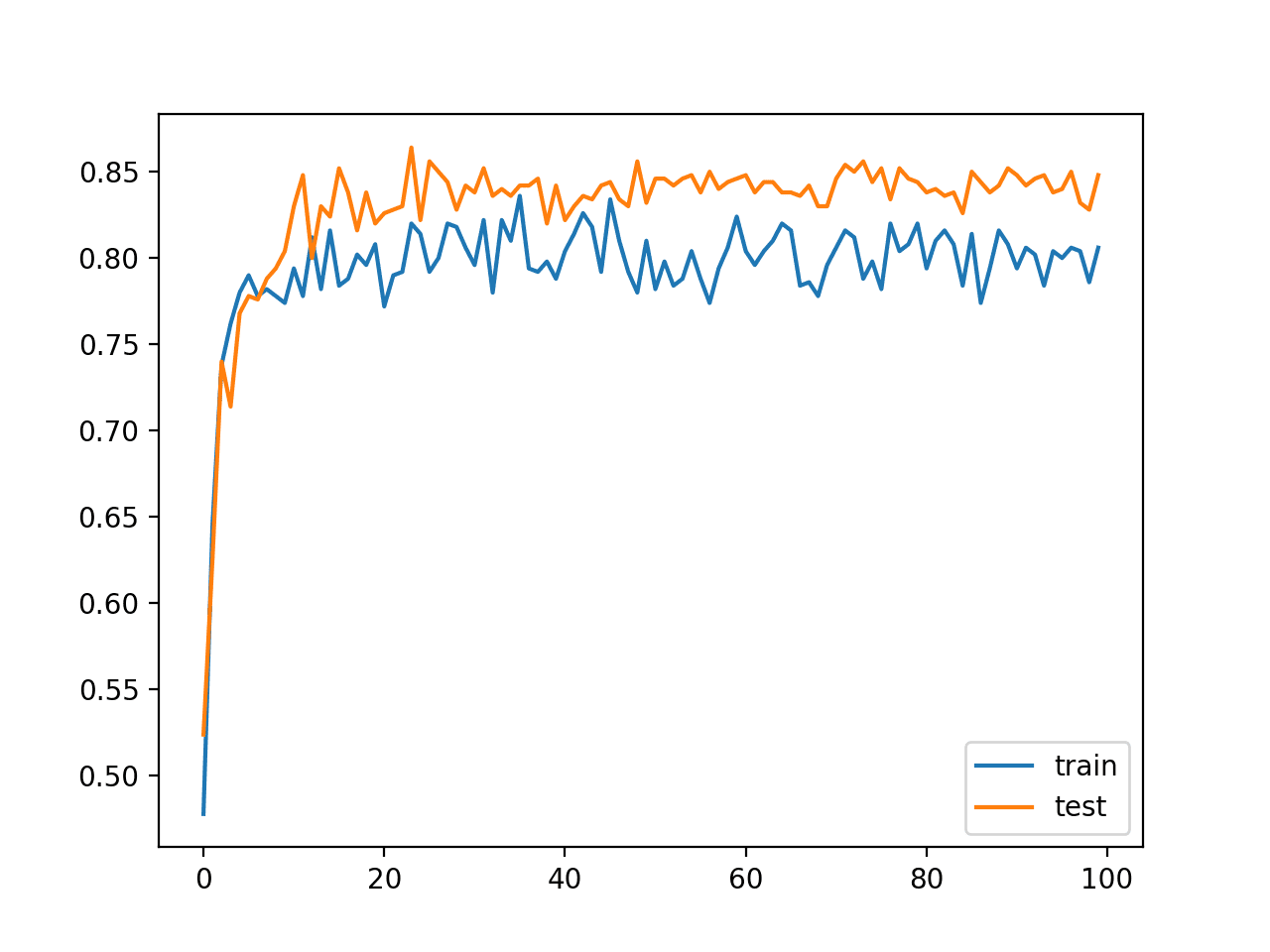
In the 2015 paper that introduced the technique titled “Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift,” the authors Sergey Ioffe and Christian Szegedy from Google demonstrated a dramatic speedup of an Inception-based convolutional neural network for photo classification over a baseline method.
By only using Batch Normalization […], we match the accuracy of Inception in less than half the number of training steps.
Kaiming He, et al. in their 2015 paper titled “Deep Residual Learning for Image Recognition” used batch normalization after the convolutional layers in their very deep model referred to as ResNet and achieve then state-of-the-art results on the ImageNet dataset, a standard photo classification task.
We adopt batch normalization (BN) right after each convolution and before activation …
Christian Szegedy, et al. from Google in their 2016 paper titled “Rethinking the Inception Architecture for Computer Vision” used batch normalization in their updated inception model referred to as GoogleNet Inception-v3, achieving then state-of-the-art results on the ImageNet dataset.
BN-auxiliary refers to the version in which the fully connected layer of the auxiliary classifier is also batch-normalized, not just the convolutions.
Dario Amodei from Baidu in their 2016 paper titled “Deep Speech 2 : End-to-End Speech Recognition in English and Mandarin” use a variation of batch normalization recurrent neural networks in their end-to-end deep model for speech recognition.
… we find that when applied to very deep networks of RNNs on large data sets, the variant of BatchNorm we use substantially improves final generalization error in addition to accelerating training
Tips for Using Batch Normalization
This section provides tips and suggestions for using batch normalization with your own neural networks.
Use With Different Network Types
Batch normalization is a general technique that can be used to normalize the inputs to a layer.
It can be used with most network types, such as Multilayer Perceptrons, Convolutional Neural Networks and Recurrent Neural Networks.
Probably Use Before the Activation
Batch normalization may be used on the inputs to the layer before or after the activation function in the previous layer.
It may be more appropriate after the activation function if for s-shaped functions like the hyperbolic tangent and logistic function.
It may be appropriate before the activation function for activations that may result in non-Gaussian distributions like the rectified linear activation function, the modern default for most network types.
The goal of Batch Normalization is to achieve a stable distribution of activation values throughout training, and in our experiments we apply it before the nonlinearity since that is where matching the first and second moments is more likely to result in a stable distribution
— Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift, 2015.
Perhaps test both approaches with your network.
Use Large Learning Rates
Using batch normalization makes the network more stable during training.
This may require the use of much larger than normal learning rates, that in turn may further speed up the learning process.
In a batch-normalized model, we have been able to achieve a training speedup from higher learning rates, with no ill side effects
— Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift, 2015.
The faster training also means that the decay rate used for the learning rate may be increased.
Less Sensitive to Weight Initialization
Deep neural networks can be quite sensitive to the technique used to initialize the weights prior to training.
The stability to training brought by batch normalization can make training deep networks less sensitive to the choice of weight initialization method.
Alternate to Data Preparation
Batch normalization could be used to standardize raw input variables that have differing scales.
If the mean and standard deviations calculated for each input feature are calculated over the mini-batch instead of over the entire training dataset, then the batch size must be sufficiently representative of the range of each variable.
It may not be appropriate for variables that have a data distribution that is highly non-Gaussian, in which case it might be better to perform data scaling as a pre-processing step.
Don’t Use With Dropout
Batch normalization offers some regularization effect, reducing generalization error, perhaps no longer requiring the use of dropout for regularization.
Removing Dropout from Modified BN-Inception speeds up training, without increasing overfitting.
— Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift, 2015.
Further, it may not be a good idea to use batch normalization and dropout in the same network.
The reason is that the statistics used to normalize the activations of the prior layer may become noisy given the random dropping out of nodes during the dropout procedure.
Batch normalization also sometimes reduces generalization error and allows dropout to be omitted, due to the noise in the estimate of the statistics used to normalize each variable.
— Page 425, Deep Learning, 2016.
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Books
- Section – 8.7.1 Batch Normalization, Deep Learning, 2016.
- Section 7.3.1. Advanced architecture patterns, Deep Learning With Python, 2017.
Papers
- Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift, 2015.
- Batch Renormalization: Towards Reducing Minibatch Dependence in Batch-Normalized Models, 2017.
- How Does Batch Normalization Help Optimization? (No, It Is Not About Internal Covariate Shift), 2018.
Articles
- Batch normalization, Wikipedia.
- Why Does Batch Norm Work?, deeplearning.ai, Video
- Batch Normalization, OpenAI, 2016.
- Batch Normalization before or after ReLU?, Reddit.
Summary
In this post, you discovered the batch normalization method used to accelerate the training of deep learning neural networks.
Specifically, you learned:
- Deep neural networks are challenging to train, not least because the input from prior layers can change after weight updates.
- Batch normalization is a technique to standardize the inputs to a network, applied to ether the activations of a prior layer or inputs directly.
- Batch normalization accelerates training, in some cases by halving the epochs or better, and provides some regularization, reducing generalization error.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.






Thanks for sharing such nice useful content !! I appreciate .
Thanks, I’m glad that you found it useful!
thanks for the great sharing with us.
Thanks, I’m glad the tutorials are helpful!
This is awesome! By far the most comprehensive discussion I have ever read about batchnorm. Thanks for sharing this!
Thanks Wei!
Hi Dr. Brownlee,
I got stuck while reading the batch norm paper at this paragraph that said
“For example, consider a layer
with the input u that adds the learned bias b, and normalizes the result by subtracting the mean of the activation
computed over the training data: xb = x − E[x]. If a gradient
descent step ignores the dependence of E[x] on b, then it
will update b ← b + ∆b, where ∆b ∝ −∂ℓ/∂xb. Then
u + (b + ∆b) − E[u + (b + ∆b)] = u + b − E[u + b].
Thus, the combination of the update to b and subsequent
change in normalization led to no change in the output
of the layer nor, consequently, the loss. As the training
continues, b will grow indefinitely while the loss remains
fixed. This problem can get worse if the normalization not
only centers but also scales the activations.”
If I interpret correctly, this says that how much ever the value of the bias increases, the output of the layer won’t change. i even tried out with the weight multiplication and the bias term in numpy and the standardization of the W*x+b term produces the same output even when i changed the weight and bias values as would happen during gradient descent. Could you please explain a bit more about what the paper is trying to say about this effect? Thank you.
Nice observation!
Thanks for the suggestion, perhaps in a future post.
Good observation
Thanks.
Hello,
I am attempting to train an LSTM NN to predict the stock price of a company eg. AAPL. In this case suppose I want to feed in the historic price data (Open,low,close,high). How would I normalize data? would batch normalization be an appropriate technique?
Perhaps compare raw vs standardized vs normalized data and see what works best for your specific dataset.
Good morning Jason!
According to this post, Batch Normalization (possibly with increased learning rate) can serve as a great acceleration technique for training deep models. Are there any known drawback of this approach? If not – do you recommend it to be applied by default by ML practitioners?
Regards!
Not really.
Yes!
Does Batch Normalization also help with Vanishing / Exploding Gradient problem?
No, it accelerates the training process.
If we normalise the inputs to each sigmoid layer, then is it possible to alleviate the saturation of sigmoid? Inputs around zero will have non-zero derivatives
Hi Sieg…Normalization will help to alleviate the saturation.
The ReLU activation function can help prevent vanishing gradients.
Batch normalization can help prevent exploding gradients, as can lowering the learning rate.
Ref: Google Crash Course.
your tutorials are very informative and very easy to follow.
Thanks!
Thanks for sharing this useful blog! I love the way you cite other resources and give your own understandings.
Thanks!
Hi Dr. Brownlee, is it acceptable to use the Batch Normalization with 3 layers deep (BGRU + 2 GRU). Basically I already did that and the results were improved in a very good way.
If it is acceptable, can you please provide me with any reference.
Use whatever works best for your model and dataset.
What role does batch normalization play in making predictions, where the batch may be only one case? Do you still use the trained scale and shift coefficients, but maybe not normalize across the units? Thanks in advance.
Yes, the coefficients are set from the training set at the end of training I believe, or the last batch of training in some cases.
Would you put batch normalisation after each layer or just a few selected layers? In convnets it seems it is a good idea to place them after each convolutional layer, what about dense layers? Finally, if you train an Autoencoder, if you use batch normalisation in the encoder, would it automatically be assumed to use it also in a decoder for symmetry?
It depends. It is best to test to see what works best for your specific model and dataset.
No, encoder-decoders do not have to be symmetrical.
Hi Jason, can you talk about how batch norm will affect inference? The official documentation on this matter is a little confusing. I’m also seeing people reporting cases that batch norm will help training but hurt inference. What’s your thought on this? Thanks.
Batch norm has parameters that are set at the end of training from the last batch or the entire training dataset, then fixed for inference.
Use whatever gives the best performance on your dataset and model.
Hi Jason, Your post helps me a lot. Thanks you so!.
You’re welcome!
HI, I have been reading a paper which basically says that the roots of the success of batch normalization is not because of reducing ICS, and that the experiments they have done proof that and the reason that it works is the relation of the optimization of landscape and smoothing the landscape
The paper: https://papers.nips.cc/paper/2018/file/905056c1ac1dad141560467e0a99e1cf-Paper.pdf
I have been wondering what do u think about this as I value ur opinion so much!
Thanks for sharing.
As you said
“Batch normalization could be used to standardize raw input variables that have differing scales. It may not be appropriate for variables that have a data distribution that is highly non-Gaussian, in which case it might be better to perform data scaling as a pre-processing step.”
is this means we can use Batch normalization before Conv layer and after Sequential() layer in CNN?
for this, we have to check each image is Guassian distribution or not?How can we do?
It can be used that way, but that is not the intent. I recommend standardising data manually prior to modeling.
If you need help preparing data, see this:
https://machinelearningmastery.com/standardscaler-and-minmaxscaler-transforms-in-python/
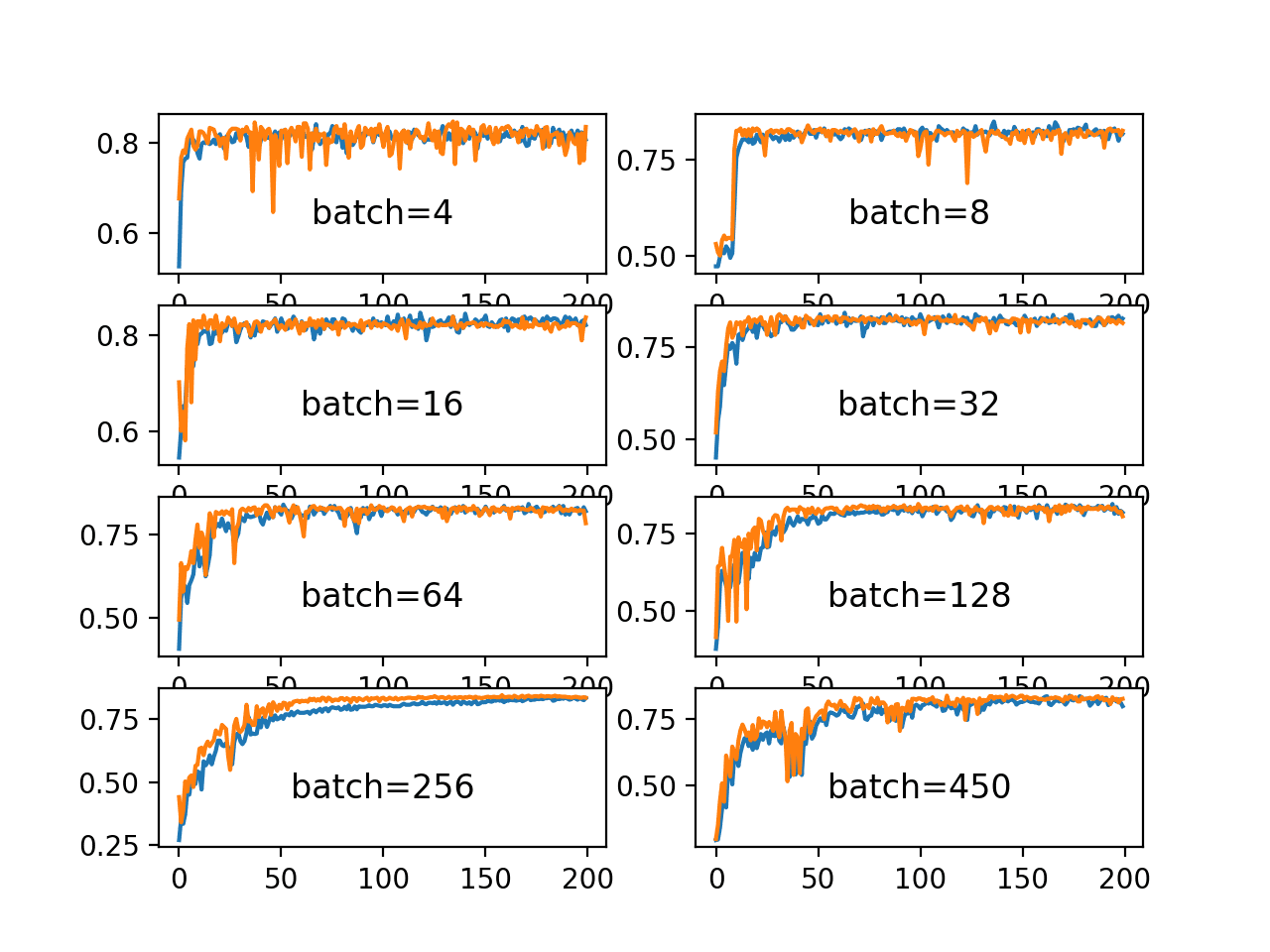
Thanks for such a nice article. I was wondering if batch normalization is useful when my batch size is larger? I assume that when using larger batches, the distribution of the data in the batches is likely to not radically change between epochs.
You’re welcome.
Perhaps. It depends on the model and on the data.
Bravooo!
Thanks!
I briefly mentioned this in the autoencoder article, but since this is focused on BN, I thought I would put this here.
I have been building an autoencoder LSTM model and was applying BN, even though my batch size was 1. My results show that even with my batch size of 1, my training was faster, my learning curves were smoother, and I could use a higher learning rate.
A few things I tweaked, which seemed to align with articles I read, were setting use_bias=False in the LSTM layer, and then applying BN before the Activation layer. I did this on layers with return_sequences=true and also for layers where return_sequences=false.
And for whatever reason, my model training was unstable when I did NOT use BN, where I would still struggle with exploding gradients.
One question still lingers: are the BN layers able to properly deal with the padded sequences and masking that I applied?
Great result, thanks for sharing.
I believe the padded inputs are filtered out by the LSTM layer before hitting the BN layer.
Thanks! Have you looked at any of the research papers where they applied BN selectively, which I assume means they built custom BN layers and applied them to the various states of the LSTM layer(s)? And if so, any thoughts on those approaches?
No, I don’t thinks no.
The ideal of applying it selectively me has me worried. I like doing the same thing to all data. As soon as I blunder in and start telling models “how”, I mess things up.
Hi, I believe whitening also requires a step that de-correlates the features, not just normalizing each individual feature such that it has mean zero and variance one. Thanks for the post!
Thanks.
Thanks the posts are really helping me to learn
You are very welcome Alagu!
This is so great. Thanks very much for your sharing.
Thank you for the feedback Rong!
This is an incredibly clear and intuitive explanation of the topic while still being detailed and precise, thank you!.
One question: You made emphasis on the fact that barchnorm is useful for very deep nets with multiple hidden layers, but I don’t see why it wouldn’t also be useful for nets with only a few layers, is there a downside to using it in shallow architectures?
Thank you for the feedback and support Sam! The following resources may be of interest to you:
https://towardsdatascience.com/curse-of-batch-normalization-8e6dd20bc304
https://medium.com/geekculture/is-batch-normalization-harmful-improving-normalizer-free-resnets-cf44f2fc0b2e