Indeterminate forms are often encountered when evaluating limits of functions, and limits in turn play an important role in mathematics and calculus. They are essential for learning about derivatives, gradients, Hessians, and a lot more.
In this tutorial, you will discover how to evaluate the limits of indeterminate forms and the L’Hospital’s rule for solving them.
After completing this tutorial, you will know:
- How to evaluate the limits of functions having indeterminate types of the form 0/0 and ∞/∞
- L’Hospital’s rule for evaluating indeterminate types
- How to convert more complex indeterminate types and apply L’Hospital’s rule to them
Let’s get started.

A Gentle Introduction to Indeterminate Forms and L’Hospital’s Rule Photo by Mehreen Saeed, some rights reserved.
Tutorial Overview
This tutorial is divided into 2 parts; they are:
- The indeterminate forms of type 0/0 and ∞/∞
- How to apply L’Hospital’s rule to these types
- Solved examples of these two indeterminate types
- More complex indeterminate types
- How to convert the more complex indeterminate types to 0/0 and ∞/∞ forms
- Solved examples of such types
Prerequisites
This tutorial requires a basic understanding of the following two topics:
If you are not familiar with these topics, you can review them by clicking the above links.
What are Indeterminate Forms?
When evaluating limits, we come across situations where the basic rules for evaluating limits might fail. For example, we can apply the quotient rule in case of rational functions:
lim(x→a) f(x)/g(x) = (lim(x→a)f(x))/(lim(x→a)g(x)) if lim(x→a)g(x)≠0
The above rule can only be applied if the expression in the denominator does not approach zero as x approaches a. A more complicated situation arises if both the numerator and denominator both approach zero as x approaches a. This is called an indeterminate form of type 0/0. Similarly, there are indeterminate forms of the type ∞/∞, given by:
lim(x→a) f(x)/g(x) = (lim(x→a)f(x))/(lim(x→a)g(x)) when lim(x→a)f(x)=∞ and lim(x→a)g(x)=∞
What is L’Hospital’s Rule?
The L’Hospital rule states the following:
When to Apply L’Hospital’s Rule
An important point to note is that L’Hospital’s rule is only applicable when the conditions for f(x) and g(x) are met. For example:
- lim(????→0) sin(x)/(x+1) Cannot apply L’Hospital’s rule as it’s not 0/0 form
- lim(????→0) sin(x)/x Can apply the rule as it’s 0/0 form
- lim(????→∞) (e^x)/(1/x+1) Cannot apply L’Hospital’s rule as it’s not ∞/∞ form
- lim(????→∞) (e^x)/x Can apply L’Hospital’s rule as it is ∞/∞ form
Examples of 0/0 and ∞/∞
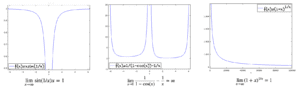
Some examples of these two types, and how to solve them are shown below. You can also refer to the figure below to refer to these functions.
Example 1.1: 0/0
Evaluate lim(????→2) ln(x-1)/(x-2) (See the left graph in the figure)
Example 1.2: ∞/∞
Evaluate lim(????→∞) ln(x)/x (See the right graph in the figure)
More Indeterminate Forms
The L’Hospital rule only tells us how to deal with 0/0 or ∞/∞ forms. However, there are more indeterminate forms that involve products, differences, and powers. So how do we deal with the rest? We can use some clever tricks in mathematics to convert products, differences and powers into quotients. This can enable us to easily apply L’Hospital rule to almost all indeterminate forms. The table below shows various indeterminate forms and how to deal with them.
Examples
The following examples show how you can convert one indeterminate form to either 0/0 or ∞/∞ form and apply L’Hospital’s rule to solve the limit. After the worked out examples you can also look at the graphs of all the functions whose limits are calculated.
Example 2.1: 0.∞
Evaluate lim(????→∞) x.sin(1/x) (See the first graph in the figure)
Example 2.2: ∞-∞
Evaluate lim(????→0) 1/(1-cos(x)) – 1/x (See the second graph in the figure below)
Example 2.3: Power form
Evaluate lim(????→∞) (1+x)^(1/x) (See the third graph in the figure below)
Extensions
This section lists some ideas for extending the tutorial that you may wish to explore.
- Cauchy’s Mean Value Theorem
- Rolle’s theorem
If you explore any of these extensions, I’d love to know. Post your findings in the comments below.
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Tutorials
Resources
- Additional resources on Calculus Books for Machine Learning
Books
- Thomas’ Calculus, 14th edition, 2017. (based on the original works of George B. Thomas, revised by Joel Hass, Christopher Heil, Maurice Weir)
- Calculus, 3rd Edition, 2017. (Gilbert Strang)
- Calculus, 8th edition, 2015. (James Stewart)
Summary
In this tutorial, you discovered the concept of indeterminate forms and how to evaluate them.
Specifically, you learned:
- Indeterminate forms of type 0/0 and ∞/∞
- L’Hospital rule for evaluating types 0/0 and ∞/∞
- Indeterminate forms of type 0.∞, ∞-∞, and power forms, and how to evaluate them.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.


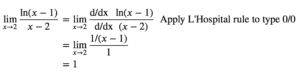



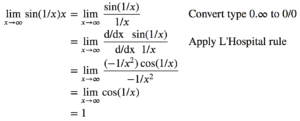
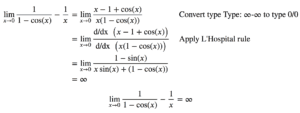







Thanks for sharing but I have a question in example 2.3 why is limit of the exponential becomes the exponential of the limit in the third equality ?
Hi Yasser
This is one of the rules for evaluating limits. Please see this article. There is a table with rules in this article:
https://machinelearningmastery.com/a-gentle-introduction-to-evaluating-limits/
Hope it helps.
Because exponential(e) is simply a constant whose value lies between 2 and 3 .And since ‘ e’ is raised to power which is a variable and gives indeterminant form as we apply limit . So the limit is only applied to the power or variable or simply the domain of the exponential function. ‘ e’ being a constant has a fixed value so there is no point of limits being applied to it .
Hello, nice post.
1) In practical ML projects- is this L’Hospital’s rule really applicable at all? I mean normally we work with data rows rather than analytical functions, so gradients are rather computed using iterative methods or extrapolations.
2) Link to “View all posts by Mehreen Saeed” seems to be broken.
Regards and good luck!
Hi, thanks for the nice post. However, I believe the correct name is “L’Hôpital” not hospital…
According to my French calculus teacher, the two spellings are equivalent and you will see both in math literature.