Training Logistic Regression with Cross-Entropy Loss in PyTorch

By Muhammad Asad Iqbal Khan on April 8, 2023 in Deep Learning with PyTorch 1

In the previous session of our PyTorch series, we demonstrated how badly initialized weights can impact the accuracy of a classification model when mean square error (MSE) loss is used. We noticed that the model didn’t converge during training and its accuracy was also significantly reduced.

In the following, you will see what happens if you randomly initialize the weights and use cross-entropy as loss function for model training. This loss function fits logistic regression and other categorical classification problems better. Therefore, cross-entropy loss is used for most of the classification problems today.

In this tutorial, you will train a logistic regression model using cross-entropy loss and make predictions on test data. Particularly, you will learn:

How to train a logistic regression model with Cross-Entropy loss in Pytorch.
How Cross-Entropy loss can influence the model accuracy.

Kick-start your project with my book Deep Learning with PyTorch. It provides self-study tutorials with working code.

Let’s get started.

Training Logistic Regression with Cross-Entropy Loss in PyTorch.
Picture by Y K. Some rights reserved.

Overview

This tutorial is in three parts; they are

Preparing the Data and Building a Model
Model Training with Cross-Entropy
Verifying with Test Data

Preparing the Data and the Model

Just like the previous tutorials, you will build a class to get the dataset to perform the experiments. This dataset will be split into train and test samples. The test samples are an unseen data used to measure the performance of the trained model.

First, we make a Dataset class:

import torch
from torch.utils.data import Dataset

# Creating the dataset class
class Data(Dataset):
    # Constructor
    def __init__(self):
        self.x = torch.arange(-2, 2, 0.1).view(-1, 1)
        self.y = torch.zeros(self.x.shape[0], 1)
        self.y[self.x[:, 0] > 0.2] = 1
        self.len = self.x.shape[0]
    # Getter
    def __getitem__(self, idx):          
        return self.x[idx], self.y[idx] 
    # getting data length
    def __len__(self):
        return self.len

import torch

from torch.utils.data import Dataset

# Creating the dataset class

class Data(Dataset):

# Constructor

def __init__(self):

self.x = torch.arange(-2, 2, 0.1).view(-1, 1)

self.y = torch.zeros(self.x.shape[0], 1)

self.y[self.x[:, 0] > 0.2] = 1

self.len = self.x.shape[0]

# Getter

def __getitem__(self, idx):

return self.x[idx], self.y[idx]

# getting data length

def __len__(self):

return self.len

Then, instantiate the dataset object.

# Creating dataset object
data_set = Data()

1 2	# Creating dataset object data_set = Data()

Next, you’ll build a custom module for our logistic regression model. It will be based on the attributes and methods from PyTorch’s nn.Module. This package allows us to build sophisticated custom modules for our deep learning models and makes the overall process a lot easier.

The module consist of only one linear layer, as follows:

# build custom module for logistic regression
class LogisticRegression(torch.nn.Module):    
    # build the constructor
    def __init__(self, n_inputs):
        super().__init__()
        self.linear = torch.nn.Linear(n_inputs, 1)
    # make predictions
    def forward(self, x):
        y_pred = torch.sigmoid(self.linear(x))
        return y_pred

# build custom module for logistic regression

class LogisticRegression(torch.nn.Module):

# build the constructor

def __init__(self, n_inputs):

super().__init__()

self.linear = torch.nn.Linear(n_inputs, 1)

# make predictions

def forward(self, x):

y_pred = torch.sigmoid(self.linear(x))

return y_pred

Let’s create the model object.

log_regr = LogisticRegression(1)

1	log_regr = LogisticRegression(1)

This model should have randomized weights. You can check this by printing its states:

print("checking parameters: ", log_regr.state_dict())

1	print("checking parameters: ", log_regr.state_dict())

You may see:

checking parameters:  OrderedDict([('linear.weight', tensor([[-0.0075]])), ('linear.bias', tensor([0.5364]))])

1	checking parameters: OrderedDict([('linear.weight', tensor([[-0.0075]])), ('linear.bias', tensor([0.5364]))])

Want to Get Started With Deep Learning with PyTorch?

Take my free email crash course now (with sample code).

Click to sign-up and also get a free PDF Ebook version of the course.

Model Training with Cross-Entropy

Recall that this model didn’t converge when you used these parameter values with MSE loss in the previous tutorial. Let’s see what happens when cross-entropy loss is used.

Since you are performing logistic regression with one output, it is a classification problem with two classes. In other words, it is a binary classification problem and hence we are using binary cross-entropy. You set up the optimizer and the loss function as follows.

...
optimizer = torch.optim.SGD(log_regr.parameters(), lr=2)
# binary cross-entropy
criterion = torch.nn.BCELoss()

...

optimizer = torch.optim.SGD(log_regr.parameters(), lr=2)

# binary cross-entropy

criterion = torch.nn.BCELoss()

Next, we prepare a DataLoader and train the model for 50 epochs.

# load data into the dataloader
train_loader = DataLoader(dataset=data_set, batch_size=2)
# Train the model
Loss = []
epochs = 50
for epoch in range(epochs):
    for x,y in train_loader:
        y_pred = log_regr(x)
        loss = criterion(y_pred, y)
        Loss.append(loss.item())
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()   
    print(f"epoch = {epoch}, loss = {loss}")
print("Done!")

# load data into the dataloader

train_loader = DataLoader(dataset=data_set, batch_size=2)

# Train the model

Loss = []

epochs = 50

for epoch in range(epochs):

for x,y in train_loader:

y_pred = log_regr(x)

loss = criterion(y_pred, y)

Loss.append(loss.item())

optimizer.zero_grad()

loss.backward()

optimizer.step()

print(f"epoch = {epoch}, loss = {loss}")

print("Done!")

The output during training would be like the following:

checking weights:  OrderedDict([('linear.weight', tensor([[-5.]])), ('linear.bias', tensor([-10.]))])

1	checking weights: OrderedDict([('linear.weight', tensor([[-5.]])), ('linear.bias', tensor([-10.]))])

As you can see, the loss reduces during the training and converges to a minimum. Let’s also plot the training graph.

import matplotlib.pyplot as plt

plt.plot(Loss)
plt.xlabel("no. of iterations")
plt.ylabel("total loss")
plt.show()

import matplotlib.pyplot as plt

plt.plot(Loss)

plt.xlabel("no. of iterations")

plt.ylabel("total loss")

plt.show()

You shall see the following: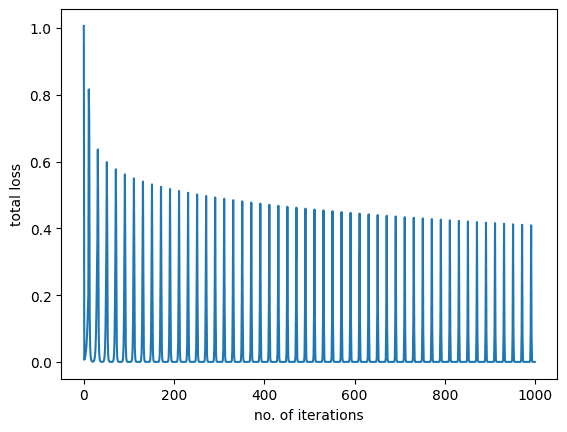

Verifying with Test Data

The plot above shows that the model learned well on the training data. Lastly, let’s check how the model performs on unseen data.

# get the model predictions on test data
y_pred = log_regr(data_set.x)
label = y_pred > 0.5 # setting the threshold between zero and one.
print("model accuracy on test data: ",
      torch.mean((label == data_set.y.type(torch.ByteTensor)).type(torch.float)))

# get the model predictions on test data

y_pred = log_regr(data_set.x)

label = y_pred > 0.5 # setting the threshold between zero and one.

print("model accuracy on test data: ",

torch.mean((label == data_set.y.type(torch.ByteTensor)).type(torch.float)))

which gives

model accuracy on test data:  tensor(1.)

1	model accuracy on test data: tensor(1.)

When the model is trained on MSE loss, it didn’t do well. It was around 57% accurate previously. But here, we get a perfect prediction. Partially because the model is simple, a one-variable logsitic function. Partially because we set up the training correctly. Hence the cross-entropy loss significantly improves the model accuracy over MSE loss as we demonstrated in our experiments.

Putting everything together, the following is the complete code:

import matplotlib.pyplot as plt 
import torch
from torch.utils.data import Dataset, DataLoader
torch.manual_seed(0)

# Creating the dataset class
class Data(Dataset):
    def __init__(self):
        self.x = torch.arange(-2, 2, 0.1).view(-1, 1)
        self.y = torch.zeros(self.x.shape[0], 1)
        self.y[self.x[:, 0] > 0.2] = 1
        self.len = self.x.shape[0]

    def __getitem__(self, idx):          
        return self.x[idx], self.y[idx] 

    def __len__(self):
        return self.len

# building dataset object
data_set = Data()

# build custom module for logistic regression
class LogisticRegression(torch.nn.Module):    
    # build the constructor
    def __init__(self, n_inputs):
        super().__init__()
        self.linear = torch.nn.Linear(n_inputs, 1)
    # make predictions
    def forward(self, x):
        y_pred = torch.sigmoid(self.linear(x))
        return y_pred

log_regr = LogisticRegression(1)
print("checking parameters: ", log_regr.state_dict())

optimizer = torch.optim.SGD(log_regr.parameters(), lr=2)
# binary cross-entropy
criterion = torch.nn.BCELoss()

# load data into the dataloader
train_loader = DataLoader(dataset=data_set, batch_size=2)
# Train the model
Loss = []
epochs = 50
for epoch in range(epochs):
    for x,y in train_loader:
        y_pred = log_regr(x)
        loss = criterion(y_pred, y)
        Loss.append(loss.item())
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()   
    print(f"epoch = {epoch}, loss = {loss}")
print("Done!")

plt.plot(Loss)
plt.xlabel("no. of iterations")
plt.ylabel("total loss")
plt.show()

# get the model predictions on test data
y_pred = log_regr(data_set.x)
label = y_pred > 0.5 # setting the threshold between zero and one.
print("model accuracy on test data: ",
      torch.mean((label == data_set.y.type(torch.ByteTensor)).type(torch.float)))