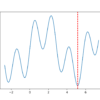
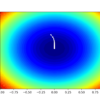
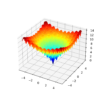
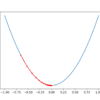
Function optimization is a field of study that seeks an input to a function that results in the maximum or minimum output of the function. There are a large number of optimization algorithms and it is important to study and develop intuitions for optimization algorithms on simple and easy-to-visualize test functions. One-dimensional functions take a […]