Loss Functions in TensorFlow

The loss metric is very important for neural networks. As all machine learning models are one optimization problem or another, the loss is the objective function to minimize. In neural networks, the optimization is done with gradient descent and backpropagation. But what are loss functions, and how are they affecting your neural networks?

In this post, you will learn what loss functions are and delve into some commonly used loss functions and how you can apply them to your neural networks.

After reading this article, you will learn:

• What are loss functions, and how they are different from metrics
• Common loss functions for regression and classification problems
• How to use loss functions in your TensorFlow model

Let’s get started!

Loss functions in TensorFlow
Photo by Ian Taylor. Some rights reserved.

Overview

This article is divided into five sections; they are:

• What are loss functions?
• Mean absolute error
• Mean squared error
• Categorical cross-entropy
• Loss functions in practice

What Are Loss Functions?

In neural networks, loss functions help optimize the performance of the model. They are usually used to measure some penalty that the model incurs on its predictions, such as the deviation of the prediction away from the ground truth label. Loss functions are usually differentiable across their domain (but it is allowed that the gradient is undefined only for very specific points, such as x = 0, which is basically ignored in practice). In the training loop, they are differentiated with respect to parameters, and these gradients are used for your backpropagation and gradient descent steps to optimize your model on the training set.

Loss functions are also slightly different from metrics. While loss functions can tell you the performance of our model, they might not be of direct interest or easily explainable by humans. This is where metrics come in. Metrics such as accuracy are much more useful for humans to understand the performance of a neural network even though they might not be good choices for loss functions since they might not be differentiable.

In the following, let’s explore some common loss functions: the mean absolute error, mean squared error, and categorical cross entropy.

Mean Absolute Error

The mean absolute error (MAE) measures the absolute difference between predicted values and the ground truth labels and takes the mean of the difference across all training examples. Mathematically, it is equal to $\frac{1}{m}\sum_{i=1}^m\lvert\hat{y}_i–y_i\rvert$ where $m$ is the number of training examples and $y_i$ and $\hat{y}_i$ are the ground truth and predicted values, respectively, averaged over all training examples.

The MAE is never negative and would be zero only if the prediction matched the ground truth perfectly. It is an intuitive loss function and might also be used as one of your metrics, specifically for regression problems, since you want to minimize the error in your predictions.

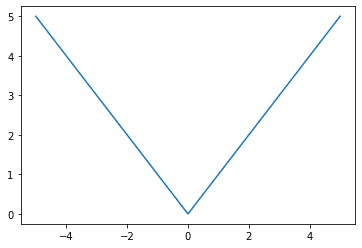
Let’s look at what the mean absolute error loss function looks like graphically:

Mean absolute error loss function, ground truth at x = 0 and x-axis represent the predicted value

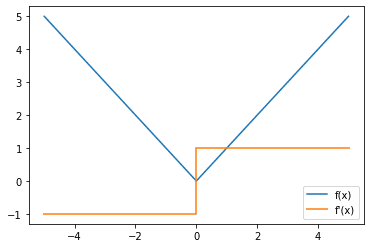
Similar to activation functions, you might also be interested in what the gradient of the loss function looks like since you are using the gradient later to do backpropagation to train your model’s parameters.

Mean absolute error loss function (blue) and gradient (orange)

You might notice a discontinuity in the gradient function for the mean absolute loss function. Many tend to ignore it since it occurs only at x = 0, which, in practice, rarely happens since it is the probability of a single point in a continuous distribution.

Let’s take a look at how to implement this loss function in TensorFlow using the Keras losses module:

This gives you 2.0 as the output as expected, since $ \frac{1}{2}(\lvert 2-1\rvert + \lvert 3-0\rvert) = \frac{1}{2}(4) = 4 $. Next, let’s explore another loss function for regression models with slightly different properties, the mean squared error.

Mean Squared Error

Another popular loss function for regression models is the mean squared error (MSE), which is equal to $\frac{1}{m}\sum_{i=1}^m(\hat{y}_i–y_i)^2$. It is similar to the mean absolute error as it also measures the deviation of the predicted value from the ground truth value. However, the mean squared error squares this difference (always non-negative since squares of real numbers are always non-negative), which gives it slightly different properties.

One notable one is that the mean squared error favors a large number of small errors over a small number of large errors, which leads to models with fewer outliers or at least outliers that are less severe than models trained with a mean absolute error. This is because a large error would have a significantly larger impact on the error and, consequently, the gradient of the error when compared to a small error.

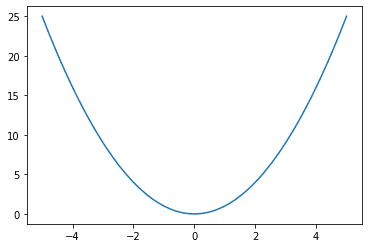
Graphically,

Mean squared error loss function, ground truth at x = 0 and x-axis represent the predicted value

Then, looking at the gradient,

Mean squared error loss function (blue) and gradient (orange)

Notice that larger errors would lead to a larger magnitude for the gradient and a larger loss. Hence, for example, two training examples that deviate from their ground truths by 1 unit would lead to a loss of 2, while a single training example that deviates from its ground truth by 2 units would lead to a loss of 4, hence having a larger impact.

Let’s look at how to implement the mean squared loss in TensorFlow.

This gives the output 5.0 as expected since $\frac{1}{2}[(2-1)^2 + (3-0)^2] = \frac{1}{2}(10) = 5$. Notice that the second example with a predicted value of 3 and actual value of 0 contributes 90% of the error under the mean squared error vs. 75% under the mean absolute error.

Sometimes, you may see people use root mean squared error (RMSE) as a metric. This will take the square root of MSE. From the perspective of a loss function, MSE and RMSE are equivalent.

Both MAE and MSE measure values in a continuous range. Hence they are for regression problems. For classification problems, you can use categorical cross-entropy.

Categorical Cross-Entropy

The previous two loss functions are for regression models, where the output could be any real number. However, for classification problems, there is a small, discrete set of numbers that the output could take. Furthermore, the number used to label-encode the classes is arbitrary and with no semantic meaning (e.g., using the labels 0 for cat, 1 for dog, and 2 for horse does not represent that a dog is half cat and half horse). Therefore, it should not have an impact on the performance of the model.

In a classification problem, the model’s output is a vector of probability for each category. In Keras models, this vector is usually expected to be “logits,” i.e., real numbers to be transformed to probability using the softmax function or the output of a softmax activation function.

The cross-entropy between two probability distributions is a measure of the difference between the two probability distributions. Precisely, it is $-\sum_i P(X = x_i) \log Q(X = x_i)$ for probability $P$ and $Q$. In machine learning, we usually have the probability $P$ provided by the training data and $Q$ predicted by the model, in which $P$ is 1 for the correct class and 0 for every other class. The predicted probability $Q$, however, is usually valued between 0 and 1. Hence when used for classification problems in machine learning, this formula can be simplified into: $$\text{categorical cross entropy} = – \log p_{gt}$$ where $p_{gt}$ is the model-predicted probability of the ground truth class for that particular sample.

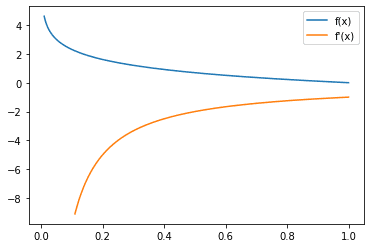
Cross-entropy metrics have a negative sign because $\log(x)$ tends to negative infinity as $x$ tends to zero. We want a higher loss when the probability approaches 0 and a lower loss when the probability approaches 1. Graphically,

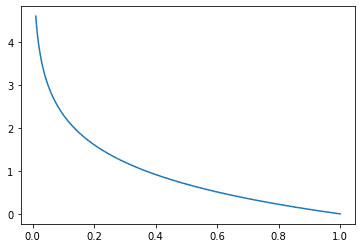
Categorical cross entropy loss function, where x is the predicted probability of the ground truth class

Notice that the loss is exactly 0 if the probability of the ground truth class is 1 as desired. Also, as the probability of the ground truth class tends to 0, the loss tends to positive infinity as well, hence substantially penalizing bad predictions. You might recognize this loss function for logistic regression, which is similar except the logistic regression loss is specific to the case of binary classes.

Now, looking at the gradient of the cross entropy loss,

Categorical cross entropy loss function (blue) and gradient (orange)

Looking at the gradient, you can see that the gradient is generally negative, which is also expected since, to decrease this loss, you would want the probability on the ground truth class to be as high as possible. Recall that gradient descent goes in the opposite direction of the gradient.

There are two different ways to implement categorical cross entropy in TensorFlow. The first method takes in one-hot vectors as input:

This gives the output as 0.2876821 which is equal to $-log(0.75)$ as expected. The other way of implementing the categorical cross entropy loss in TensorFlow is using a label-encoded representation for the class, where the class is represented by a single non-negative integer indicating the ground truth class instead.

This likewise gives the output 0.2876821.

Now that you’ve explored loss functions for both regression and classification models, let’s take a look at how you can use loss functions in your machine learning models.

Loss Functions in Practice

Let’s explore how to use loss functions in practice. You’ll explore this through a simple dense model on the MNIST digit classification dataset.

First, download the data from the Keras datasets module:

Then, build your model:

And look at the model architecture outputted from the above code:

You can then compile your model, which is also where you introduce the loss function. Since this is a classification problem, use the cross entropy loss. In particular, since the MNIST dataset in Keras datasets is represented as a label instead of a one-hot vector, use the SparseCategoricalCrossEntropy loss.

And finally, you train your model:

And your model successfully trains with the following output:

And that’s one example of how to use a loss function in a TensorFlow model.

Further Reading

Below is some documentation on loss functions from TensorFlow/Keras:

• Mean absolute error: https://www.tensorflow.org/api_docs/python/tf/keras/losses/MeanAbsoluteError
• Mean squared error: https://www.tensorflow.org/api_docs/python/tf/keras/losses/MeanSquaredError
• Categorical cross entropy: https://www.tensorflow.org/api_docs/python/tf/keras/losses/CategoricalCrossentropy
• Sparse categorical cross entropy: https://www.tensorflow.org/api_docs/python/tf/keras/losses/SparseCategoricalCrossentropy

Conclusion

In this post, you have seen loss functions and the role that they play in a neural network. You have also seen some popular loss functions used in regression and classification models, as well as how to use the cross entropy loss function in a TensorFlow model.

Specifically, you learned:

• What are loss functions, and how they are different from metrics
• Common loss functions for regression and classification problems
• How to use loss functions in your TensorFlow model