PyTorch library is for deep learning. Some applications of deep learning models are to solve regression or classification problems.
In this post, you will discover how to use PyTorch to develop and evaluate neural network models for binary classification problems.
After completing this post, you will know:
How to load training data and make it available to PyTorch
How to design and train a neural network
How to evaluate the performance of a neural network model using k-fold cross validation
How to run a model in inference mode
How to create receiver operating characteristics curve for a binary classification model
Kick-start your project with my book Deep Learning with PyTorch. It provides self-study tutorials with working code.
Let’s get started.
Building a Binary Classification Model in PyTorch Photo by David Tang. Some rights reserved.
Description of the Dataset
The dataset you will use in this tutorial is the Sonar dataset.
This is a dataset that describes sonar chirp returns bouncing off different services. The 60 input variables are the strength of the returns at different angles. It is a binary classification problem that requires a model to differentiate rocks from metal cylinders.
It is a well-understood dataset. All the variables are continuous and generally in the range of 0 to 1. The output variable is a string “M” for mine and “R” for rock, which will need to be converted to integers 1 and 0.
A benefit of using this dataset is that it is a standard benchmark problem. This means that we have some idea of the expected skill of a good model. Using cross-validation, a neural network should be able to achieve a performance of 84% to 88% accuracy.
Load the Dataset
If you have downloaded the dataset in CSV format and saved it as sonar.csv in the local directory, you can load the dataset using pandas. There are 60 input variables (X) and one output variable (y). Because the file contains mixed data of strings and numbers, it is easier to read them using pandas rather than other tools such as NumPy.
Data can be read as follows:
1
2
3
4
5
6
import pandas aspd
# Read data
data=pd.read_csv("sonar.csv",header=None)
X=data.iloc[:,0:60]
y=data.iloc[:,60]
It is a binary classification dataset. You would prefer a numeric label over a string label. You can do such conversion with LabelEncoder in scikit-learn. The LabelEncoder is to map each label to an integer. In this case, there are only two labels and they will become 0 and 1.
Using it, you need to first call the fit() function to make it learn what labels are available. Then call transform() to do the actual conversion. Below is how you use LabelEncoder to convert y from strings into 0 and 1:
1
2
3
4
5
from sklearn.preprocessing import LabelEncoder
encoder=LabelEncoder()
encoder.fit(y)
y=encoder.transform(y)
You can see the labels using:
1
print(encoder.classes_)
which outputs:
1
['M' 'R']
and if you run print(y), you would see the following
You see the labels are converted into 0 and 1. From the encoder.classes_, you know that 0 means “M” and 1 means “R”. They are also called the negative and positive classes respectively in the context of binary classification.
Afterward, you should convert them into PyTorch tensors as this is the format a PyTorch model would like to work with.
Want to Get Started With Deep Learning with PyTorch?
Take my free email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Creating a Model
Now you’re ready for the neural network model.
As you have seen in some previous posts, the easiest neural network model is a 3-layer model that has only one hidden layer. A deep learning model is usually referring to those with more than one hidden layer. All neural network models have parameters called weights. The more parameters a model has, heuristically we believe that it is more powerful. Should you use a model with fewer layers but more parameters on each layer, or a model with more layers but less parameters each? Let’s find out.
A model with more parameters on each layer is called a wider model. In this example, the input data has 60 features to predict one binary variable. You can assume to make a wide model with one hidden layer of 180 neurons (three times the input features). Such model can be built using PyTorch:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
import torch.nn asnn
classWide(nn.Module):
def __init__(self):
super().__init__()
self.hidden=nn.Linear(60,180)
self.relu=nn.ReLU()
self.output=nn.Linear(180,1)
self.sigmoid=nn.Sigmoid()
def forward(self,x):
x=self.relu(self.hidden(x))
x=self.sigmoid(self.output(x))
returnx
Because it is a binary classification problem, the output have to be a vector of length 1. Then you also want the output to be between 0 and 1 so you can consider that as probability or the model’s confidence of prediction that the input corresponds to the “positive” class.
A model with more layer is called a deeper model. Considering that the previous model has one layer with 180 neurons, you can try one with three layers of 60 neurons each instead. Such model can be built using PyTorch:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
classDeep(nn.Module):
def __init__(self):
super().__init__()
self.layer1=nn.Linear(60,60)
self.act1=nn.ReLU()
self.layer2=nn.Linear(60,60)
self.act2=nn.ReLU()
self.layer3=nn.Linear(60,60)
self.act3=nn.ReLU()
self.output=nn.Linear(60,1)
self.sigmoid=nn.Sigmoid()
def forward(self,x):
x=self.act1(self.layer1(x))
x=self.act2(self.layer2(x))
x=self.act3(self.layer3(x))
x=self.sigmoid(self.output(x))
returnx
You can confirm that these two models are having similar number of parameters, as follows:
There will be all the model’s parameters returned by model1.parameters() and each is a PyTorch tensors. Then you can reformat each tensor into a vector and count the length of the vector, using x.reshape(-1).shape[0]. So the above sum up the total number of parameters in each model.
Comparing Models with Cross-Validation
Should you use a wide model or a deep model? One way to tell is to use cross-validation to compare them.
It is a technique that, use a “training set” of data to train the model and then use a “test set” of data to see how accurate the model can predict. The result from test set is what you should focus on. But you do not want to test a model once because if you see an extremely good or bad result, it may be by chance. You want to run this process $k$ times with different training and test sets, such that you are ensured that you are comparing the **model design**, not the result of a particular training.
The technique that you can use here is called k-fold cross validation. It is to split a larger dataset into $k$ portions and take one portion as the test set while the $k-1$ portions are combined as the training set. There are $k$ different such combinations. Therefore you can repeat the experiment for $k$ times and take the average result.
In scikit-learn, you have a function for stratified k-fold. Stratified means that when the data is split into $k$ portions, the algorithm will look at the labels (i.e., the positive and negative classes in a binary classification problem) to ensure it is split in such a way that each portion contains equal number of either classes.
Running k-fold cross validation is trivial, such as the following:
Simply speaking, you use StratifiedKFold() from scikit-learn to split the dataset. This function returns to you the indices. Hence you can create the splitted dataset using X[train] and X[test] and named them training set and validation set (so it is not confused with “test set” which will be used later, after we picked our model design). You assume to have a function that runs the training loop on a model and give you the accuracy on the validation set. You can than find the mean and standard deviation of this score as the performance metric of such model design. Note that you need to create a new model every time in the for-loop above because you should not re-train a trained model in the k-fold cross valiation.
with tqdm.tqdm(batch_start,unit="batch",mininterval=0,disable=True)asbar:
bar.set_description(f"Epoch {epoch}")
forstart inbar:
# take a batch
X_batch=X_train[start:start+batch_size]
y_batch=y_train[start:start+batch_size]
# forward pass
y_pred=model(X_batch)
loss=loss_fn(y_pred,y_batch)
# backward pass
optimizer.zero_grad()
loss.backward()
# update weights
optimizer.step()
# print progress
acc=(y_pred.round()==y_batch).float().mean()
bar.set_postfix(
loss=float(loss),
acc=float(acc)
)
# evaluate accuracy at end of each epoch
model.eval()
y_pred=model(X_val)
acc=(y_pred.round()==y_val).float().mean()
acc=float(acc)
ifacc>best_acc:
best_acc=acc
best_weights=copy.deepcopy(model.state_dict())
# restore model and return best accuracy
model.load_state_dict(best_weights)
returnbest_acc
The training loop above contains the usual elements: The forward pass, the backward pass, and the gradient descent weight updates. But it is extended to have an evaluation step after each epoch: You run the model at evaluation mode and check how the model predicts the validation set. The accuracy on the validation set is remembered along with the model weight. At the end of the training, the best weight is restored to the model and the best accuracy is returned. This returned value is the best you ever encountered during the many epochs of training and it is based on the validation set.
Note that you set disable=True in the tqdm above. You can set it to False to see the training set loss and accuracy as you progress in the training.
Remind that the goal is to pick the best design and train the model again, which in the training, you want to have an evaluation score so you know what to expect in production. Thus you should split the entire dataset you obtained into a training set and test set. Then you further split the training set in k-fold cross validation.
With these, here is how you can compare the two model designs: By running k-fold cross validation on each and compare the accuracy:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
from sklearn.model_selection import StratifiedKFold,train_test_split
# train-test split: Hold out the test set for final model evaluation
So you found that the deeper model is better than the wider model, in the sense that the mean accuracy is higher and its standard deviation is lower.
Retrain the Final Model
Now you know which design to pick, you want to rebuild the model and retrain it. Usually in k-fold cross validation, you will use a smaller dataset to make the training faster. The final accuracy is not an issue because the gold of k-fold cross validation to to tell which design is better. In the final model, you want to provide more data and produce a better model, since this is what you will use in production.
As you already split the data into training and test set, these are what you will use. In Python code,
You can reuse the model_train() function as it is doing all the required training and validation. This is because the training procedure doesn’t change for the final model or during k-fold cross validation.
This model is what you can use in production. Usually it is unlike training, prediction is one data sample at a time in production. The following is how we demonstate using the model for inference by running five samples from the test set:
You run the code under torch.no_grad() context because you sure there’s no need to run the optimizer on the result. Hence you want to relieve the tensors involved from remembering how the values are computed.
The output of a binary classification neural network is between 0 and 1 (because of the sigmoid function at the end). From encoder.classes_, you can see that 0 means “M” and 1 means “R”. For a value between 0 and 1, you can simply round it to the nearest integer and interpret the 0-1 result, i.e.,
1
2
y_pred=model(X_test[i:i+1])
y_pred=y_pred.round()# 0 or 1
or use any other threshold to quantize the value into 0 or 1, i.e.,
1
2
3
threshold=0.68
y_pred=model(X_test[i:i+1])
y_pred=(y_pred>threshold).float()# 0.0 or 1.0
Indeed, round to the nearest integer is equivalent to using 0.5 as the threshold. A good model should be robust to the choice of threshold. It is when the model output exactly 0 or 1. Otherwise you would prefer a model that seldom report values in the middle but often return values close to 0 or close to 1. To see if your model is good, you can use receiver operating characteristic curve (ROC), which is to plot the true positive rate against the false positive rate of the model under various threshold. You can make use of scikit-learn and matplotlib to plot the ROC:
1
2
3
4
5
6
7
8
9
10
11
12
from sklearn.metrics import roc_curve
import matplotlib.pyplot asplt
with torch.no_grad():
# Plot the ROC curve
y_pred=model(X_test)
fpr,tpr,thresholds=roc_curve(y_test,y_pred)
plt.plot(fpr,tpr)# ROC curve = TPR vs FPR
plt.title("Receiver Operating Characteristics")
plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plt.show()
You may see the following. The curve is always start from the lower left corner and ends at upper right corner. The closer the curve to the upper left corner, the better your model is.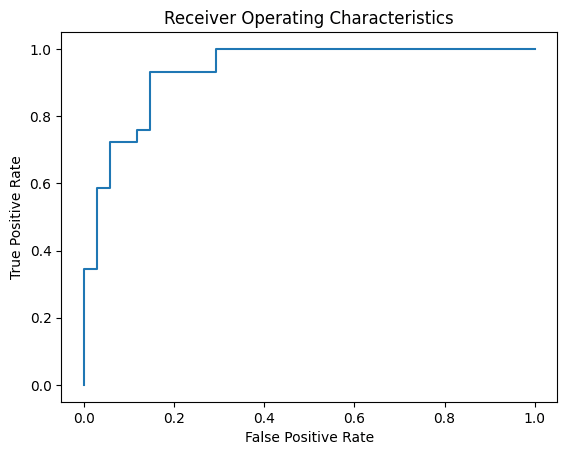
Complete Code
Putting everything together, the following is the complete code of the above:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
import copy
import matplotlib.pyplot asplt
import numpy asnp
import pandas aspd
import torch
import torch.nn asnn
import torch.optim asoptim
import tqdm
from sklearn.metrics import roc_curve
from sklearn.model_selection import StratifiedKFold,train_test_split
It provides self-study tutorials with hundreds of working code to turn you from a novice to expert. It equips you with tensor operation, training, evaluation, hyperparameter optimization,
and much more...
Kick-start your deep learning journey with hands-on exercises
Hello, there is a problem I don’t understand. In the two loops of fold.split, there is model=Wide() or Deep() at the beginning of each loop. Is this a reset of the model? If each loop continues to train the best model in the previous cycle, Whether model=Wide() or Deep() should be placed outside the loop to avoid reassignment of the model
Hello, there is a problem I don’t understand. In the two loops of fold.split, there is model=Wide() or Deep() at the beginning of each loop. Is this a reset of the model? If each loop continues to train the best model in the previous cycle, Whether model=Wide() or Deep() should be placed outside the loop to avoid reassignment of the model