Applied machine learning is challenging because the designing of a perfect learning system for a given problem is intractable.
There is no best training data or best algorithm for your problem, only the best that you can discover.
The application of machine learning is best thought of as search problem for the best mapping of inputs to outputs given the knowledge and resources available to you for a given project.
In this post, you will discover the conceptualization of applied machine learning as a search problem.
After reading this post, you will know:
- That applied machine learning is the problem of approximating an unknown underlying mapping function from inputs to outputs.
- That design decisions such as the choice of data and choice of algorithm narrow the scope of possible mapping functions that you may ultimately choose.
- That the conceptualization of machine learning as a search helps to rationalize the use of ensembles, the spot checking of algorithms and the understanding of what is happening when algorithms learn.
Kick-start your project with my new book Optimization for Machine Learning, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
A Gentle Introduction to Applied Machine Learning as a Search Problem
Photo by tonko43, some rights reserved.
Overview
This post is divided into 5 parts; they are:
- Problem of Function Approximation
- Function Approximation as Search
- Choice of Data
- Choice of Algorithm
- Implications of Machine Learning as Search
Problem of Function Approximation
Applied machine learning is the development of a learning system to address a specific learning problem.
The learning problem is characterized by observations comprised of input data and output data and some unknown but coherent relationship between the two.
The goal of the learning system is to learn a generalized mapping between input and output data such that skillful predictions can be made for new instances drawn from the domain where the output variable is unknown.
In statistical learning, a statistical perspective on machine learning, the problem is framed as the learning of a mapping function (f) given input data (X) and associated output data (y).
|
1 |
y = f(X) |
We have a sample of X and y and do our best to come up with a function that approximates f, e.g. fprime, such that we can make predictions (yhat) given new examples (Xhat) in the future.
|
1 |
yhat = fprime(Xhat) |
As such, applied machine learning can be thought of as the problem of function approximation.
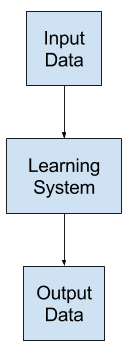
Machine learning as the mapping from inputs to outputs
The learned mapping will be imperfect.
The problem of designing and developing a learning system is the problem of learning a useful approximate of the unknown underlying function that maps the input variables to the output variables.
We do not know the form of the function, because if we did, we would not need a learning system; we could specify the solution directly.
Because we do not know the true underlying function, we must approximate it, meaning we do not know and may never know how close of an approximation the learning system is to the true mapping.
Want to Get Started With Optimization Algorithms?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Function Approximation as Search
We must search for an approximation of the true underlying function that is good enough for our purposes.
There are many sources of noise that introduce error into the learning process that can make the process more challenging and in turn result in a less useful mapping. For example:
- The choice of the framing of the learning problem.
- The choice of the observations used to train the system.
- The choice of how the training data is prepared.
- The choice of the representational form for the predictive model.
- The choice of the learning algorithm to fit the model on the training data.
- The choice of the performance measure by which to evaluate predictive skill.
And so much more.
You can see that there are many decision points in the development of a learning system, and none of the answers are known beforehand.
You can think of all possible learning systems for a learning problem as a huge search space, where each decision point narrows the search.
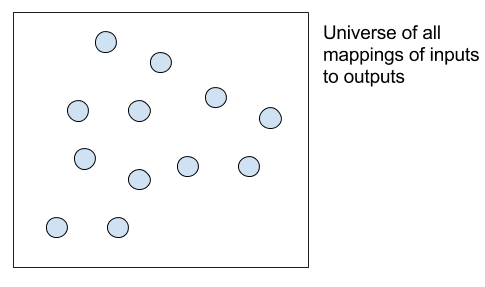
Search space of all possible mapping functions from inputs to outputs
For example, if the learning problem was to predict the species of flowers, one of millions of possible learning systems could be narrowed down as follows:
- Choose to frame the problem as predicting a species class label, e.g. classification.
- Choose measurements of the flowers of a given species and their associated sub-species.
- Choose flowers in one specific nursery to measure in order to collect training data.
- Choose a decision tree model representation so that predictions can be explained to stakeholders.
- Choose the CART algorithm to fit the decision tree model.
- Choose classification accuracy to evaluate the skill of models.
And so on.
You can also see that there may be a natural hierarchy for many of the decisions involved in developing a learning system, each of which further narrows the space of possible learning systems that we could build.
This narrowing introduces a useful bias that intentionally selects one subset of possible learning systems over another with the goal of getting closer to a useful mapping that we can use in practice. This biasing applies both at the top level in the framing of the problem and at low levels, such as the choice of machine learning algorithm or algorithm configuration.
Choice of Data
The chosen framing of the learning problem and the data used to train the system are a big point of leverage in the development of your learning system.
You do not have access to all data: that is all pairs of inputs and outputs. If you did, you would not need a predictive model in order to make output predictions for new input observations.
You do have some historical input-output pairs. If you didn’t, you would not have any data with which to train a predictive model.
But maybe you have a lot of data and you need to select only some of it for training. Or maybe you have the freedom to generate data at will and are challenged by what and how much data to generate or collect.
The data that you choose to model your learning system on must sufficiently capture the relationship between the input and output data for both the data that you have available and data that the model will be expected to make predictions on in the future.
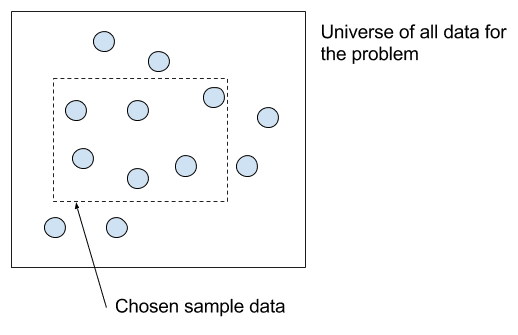
Choice of training data from the universe of all data for a problem
Choice of Algorithm
You must choose the representation of the model and the algorithm used to fit the model on the training data. This, again, is another big point of leverage on the development of your learning system.
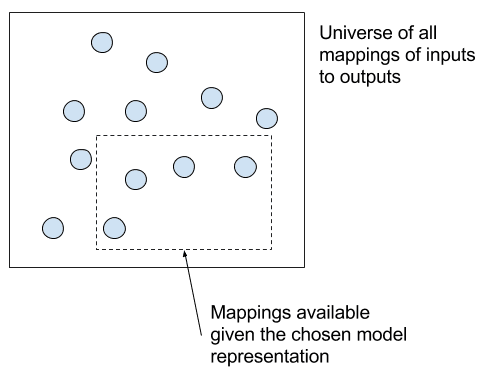
Choice of algorithm from the universe of all algorithms for a problem
Often this decision is simplified to the selection of an algorithm, although it is common for the project stakeholders to impose constraints on the project, such as the model being able to explain predictions which in turn imposes constraints on the form of the final model representation and in turn on the scope of mappings that you can search.
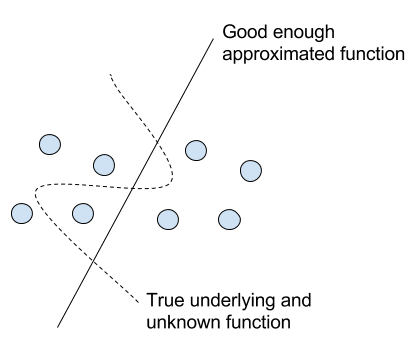
Effect of choosing an approximate mapping from inputs to outputs
Implications of Machine Learning as Search
This conceptualization of developing learning systems as a search problem helps to make clear many related concerns in applied machine learning.
This section looks at a few.
Algorithms that Learn Iteratively
The algorithm used to learn the mapping will impose further constraints, and it, along with the chosen algorithm configuration, will control how the space of possible candidate mappings is navigated as the model is fit (e.g. for machine learning algorithms that learn iteratively).
Here, we can see that the act of learning from training data by a machine learning algorithm is in effect navigating the space of possible mappings for the learning system, hopefully moving from poor mappings to better mappings (e.g. hill climbing).
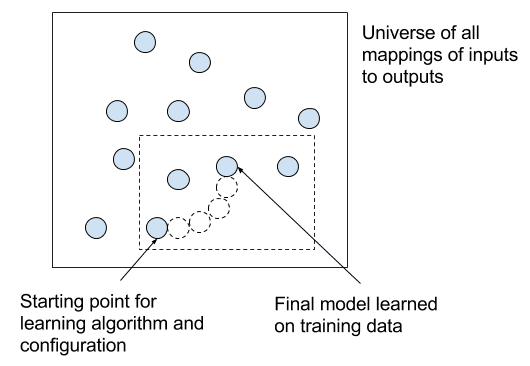
Effect of a learning algorithm iteratively training on data
This provides a conceptual rationale for the role of optimization algorithms in the heart of machine learning algorithms to get the most out of the model representation for the specific training data.
Rationale for Ensembles
We can also see that different model representations will occupy quite different locations in the space of all possible function mappings, and in turn have quite different behavior when making predictions (e.g. uncorrelated prediction errors).
This provides a conceptual rationale for the role of ensemble methods that combine the predictions from different but skillful predictive models.
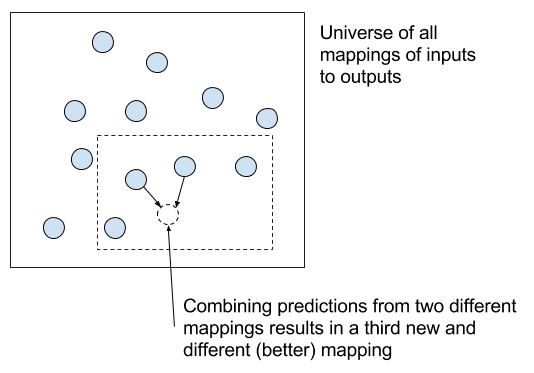
Interpretation of combining predictions from multiple final models
Rationale for Spot Checking
Different algorithms with different representations may start in different positions in the space of possible function mappings, and will navigate the space differently.
If the constrained space that these algorithms are navigating is well specified by an appropriating framing and good data, then most algorithms will likely discover good and similar mapping functions.
We can also see how a good framing and careful selection of training data can open up a space of candidate mappings that may be found by a suite of modern powerful machine learning algorithms.
This provides rationale for spot checking a suite of algorithms on a given machine learning problem and doubling down on the one that shows the most promise, or selecting the most parsimonious solution (e.g. Occam’s razor).
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
- Chapter 2, Machine Learning, 1997.
- Generalization as Search, 1982.
- Chapter 1, Data Mining: Practical Machine Learning Tools and Techniques, 2016.
- On algorithm selection, with an application to combinatorial search problems, 2012.
- Algorithm Selection on Wikipedia
Summary
In this post, you discovered the conceptualization of applied machine learning as a search problem.
Specifically, you learned:
- That applied machine learning is the problem of approximating an unknown underlying mapping function from inputs to outputs.
- That design decisions such as the choice of data and choice of algorithm narrow the scope of possible mapping functions that you may ultimately choose.
- That the conceptualization of machine learning as search helps to rationalize the use of ensembles, the spot checking of algorithms and the understanding of what is happening when algorithms learn.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.






This is a great post! I’d like to see more posts like this one. Also it would be good if you can write more about statistical methods for ML!
Thanks!
Very interesting. Made a lot of sense.
Thanks,
Roberto Cadena
Thanks Roberto.
Thanks Jason, the simplified explanations make it quite easy to understand and relate to.
tHanks, I’m glad to hear that.
Jason,
This is a great article and begs some questions, and maybe a separate blog to tell us your thoughts on this. I am seeing in my work a general shift of types of applications of ML and actual competition between different general categories of algorithms, and it seems to have a lot to do with how they are applied in terms of the type of “search” algorithms used, as you point out. In particular, I am seeing NN’s which were once confined to specific specialist tasks, like image and speech processing, are now coming to the fore based on changing configurations to compete generally with some of the best of our “classic” ML techniques (let’s say, for example, XGBoost). Has there been any systematic attempt you know of in the literature or in research to track this shifting by closely tracking the changing efficiencies as we develop new NN technologies comparing them to classic ML? The result would be that in specific instances we would know when we actually need to think about shifting our strategies for advanced analytics for benchmark cases, such as fraud detection…
Craig
Good question Craig.
It’s intractable to map techniques to problems. A small change in the input features used can dramatically change the “problem”, for example.
The best we can do is to evaluate a suite of methods on each specific problem we encounter to see what works best.
Any claims of neural nets are for “A” and xgboost is for “B” is probably anecdotal at best when it really comes down to it.
We often don’t have the resources for full evaluations, so the short cut is to use the methods that others (in the literature) have reported to work well.
Does that help?
Sir it is in High level language.How can all the people like me are going to understand.Please Try to Put In a Low level language for us to understand
Sorry to hear that. Which part don’t you understand?
Thks Jason for these fruitful ideas!
I think that ML/DL main success depend on the mathematics below !. And math can be a serious issue (when you go through very complex symbolic formulas and theorems and at that momento very really hard to follow). But also math can be approached as “intuitive” or approximative way (later you can iterate to get more deeper approach normally) as a natural tool when you explain basic or physical or analogous concepts to introduce your problem or case.
Talking about your spaces of this blog (i.e. the math below) where algorithms models (and also input/output data) “live in”, my suggestion is to introduce also maths ideas from HILBERT SPACES (https://en.wikipedia.org/wiki/Hilbert_space) with infinite dimensions and even comprising the domain of infinite functions.
That is to say, I guess everybody has the “Euclidean space “natural” concepts” such as angles, vectors, projections, dimensions (normally 3D) , metrics as distance, derived from scalar and vectors multiplication from this plane. So the intuitive force is coming from “geometric approach” …then what happens when we extrapolated to higher dimensions of 3D? and what about functions instead of numbers? or infinite dimensions instead of finite Euclidean dimensions? …that really are hard to deal with (so the symbolic and math formulas replace your natural ideas and transport you to infinite dimensions, infinite projections, … even if nobody understand it physically…So I guess Hilbert Space approach will have many thing to deal with in this data and Machine/Deep Learning approach math model/algorithms approach…
For me one of the most natural ideas coming from euclidean approach are metrics (distance of vectors) and projections (how we can break down or split something like algorithms or data into other more familiars parts …filters and convolution layers I guess do that in ML/DL…but because it has infinite dimensions, we only capture some few patterns (image, data,..) …visualize convolutions layers like this help a lot of (at least for me).
other idea for this blog, in addition of Hilbert space “logic and math approach” that has to be mentioned is the HEURISTIC approach, i.e. there is not rational or fully method to search for the best or optimal solutions, but exists many more intuitive ways that put us in front of particular solutions, even if they are not the optimal solutions at all, pending to be discovered, if they exist (because the live in an “infinite domain”) …
The math can add depth, but is not required.
I do not need to know how to design or even repair combustion engines in order to drive my car.
OK
Many thanks dear.
Really, so gentle an introduction to an applied machine learning: concise and informative!
I’m glad it helped.
Jason I’m loving your sharing of your knowledge and insights. My wife thinks I’m silly reading about this on holiday but it’s so enjoyable to be learning. I can’t thank you enough.
Thanks Nelson!
You picked a great post to read too, I’m a massive fan of the “ml as search” way of thinking.
Thanks article, Jason.
I have a lot of your materials.
Many thanks.
Thanks.
Very Precise, definitely planning to go through each and every blog.
Thanks Jason.
Thanks.