How To Use Regression Machine Learning Algorithms in Weka

Weka has a large number of regression algorithms available on the platform.

The large number of machine learning algorithms supported by Weka is one of the biggest benefits of using the platform.

In this post you will discover how to use top regression machine learning algorithms in Weka.

After reading this post you will know:

• About 5 top regression algorithms supported by Weka.
• How to use regression machine learning algorithms for predictive modeling in Weka.
• About the key configuration options of regression algorithms in Weka.

Kick-start your project with my new book Machine Learning Mastery With Weka, including step-by-step tutorials and clear screenshots for all examples.

Let’s get started.

How To Use Regression Machine Learning Algorithms in Weka
Photo by solarisgirl, some rights reserved.

Regression Algorithms Overview

We are going to take a tour of 5 top regression algorithms in Weka.

Each algorithm that we cover will be briefly described in terms of how it works, key algorithm parameters will be highlighted and the algorithm will be demonstrated in the Weka Explorer interface.

The 5 algorithms that we will review are:

1. Linear Regression
2. k-Nearest Neighbors
3. Decision Tree
4. Support Vector Machines
5. Multi-Layer Perceptron

These are 5 algorithms that you can try on your regression problem as a starting point.

A standard machine learning regression problem will be used to demonstrate each algorithm.

Specifically, the Boston House Price Dataset. Each instance describes the properties of a Boston suburb and the task is to predict the house prices in thousands of dollars. There are 13 numerical input variables with varying scales describing the properties of suburbs. You can learn more about this dataset on the UCI Machine Learning Repository.

Start the Weka Explorer:

1. Open the Weka GUI Chooser.
2. Click the “Explorer” button to open the Weka Explorer.
3. Load the Boston house price dataset from the housing.arff file.
4. Click “Classify” to open the Classify tab.

Let’s start things off by looking at the linear regression algorithm.

Linear Regression

Linear regression only supports regression type problems.

It works by estimating coefficients for a line or hyperplane that best fits the training data. It is a very simple regression algorithm, fast to train and can have great performance if the output variable for your data is a linear combination of your inputs.

It is good idea to evaluate linear regression on your problem before moving onto more complex algorithms in case it performs well.

Choose the linear regression algorithm:

1. Click the “Choose” button and select “LinearRegression” under the “functions” group.
2. Click on the name of the algorithm to review the algorithm configuration.

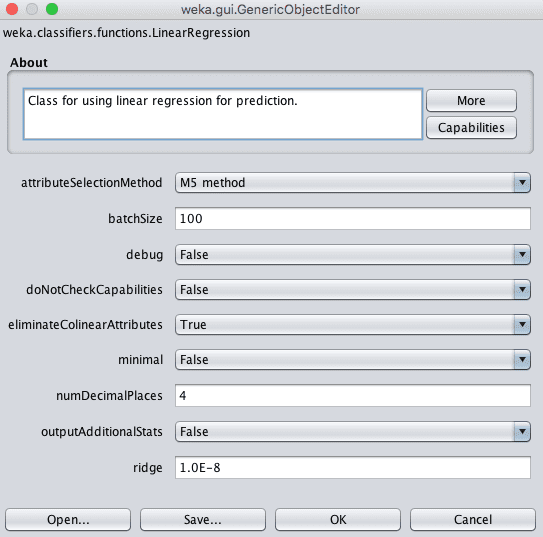
Weka Configuration of Linear Regression

The performance of linear regression can be reduced if your training data has input attributes that are highly correlated. Weka can detect and remove highly correlated input attributes automatically by setting eliminateColinearAttributes to True, which is the default.

Additionally, attributes that are unrelated to the output variable can also negatively impact performance. Weka can automatically perform feature selection to only select those relevant attributes by setting the attributeSelectionMethod. This is enabled by default and can be disabled.

Finally, the Weka implementation uses a ridge regularization technique in order to reduce the complexity of the learned model. It does this by minimizing the square of the absolute sum of the learned coefficients, which will prevent any specific coefficient from becoming too large (a sign of complexity in regression models).

1. Click “OK” to close the algorithm configuration.
2. Click the “Start” button to run the algorithm on the Boston house price dataset.

You can see that with the default configuration that linear regression achieves an RMSE of 4.9.

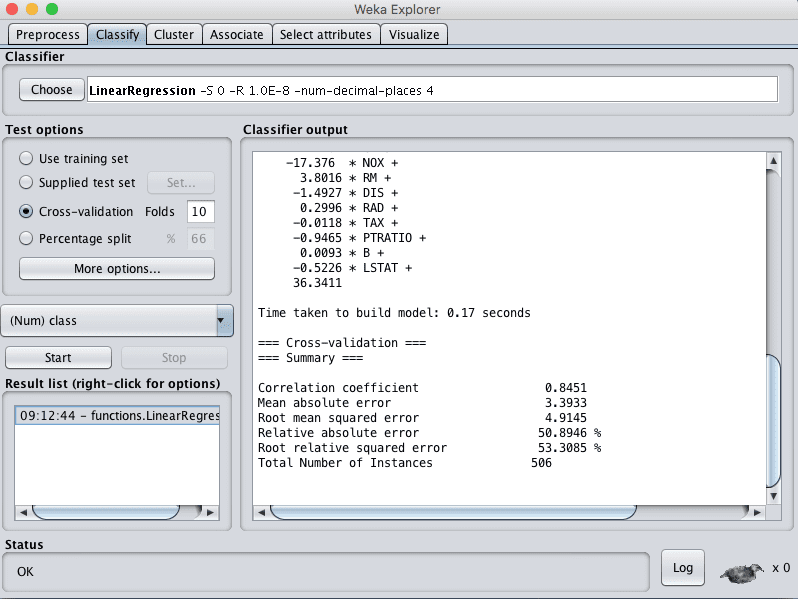
Weka Results for Linear Regression

k-Nearest Neighbors

The k-nearest neighbors algorithm supports both classification and regression. It is also called kNN for short. It works by storing the entire training dataset and querying it to locate the k most similar training patterns when making a prediction.

As such, there is no model other than the raw training dataset and the only computation performed is the querying of the training dataset when a prediction is requested.

It is a simple algorithm, but one that does not assume very much about the problem other than that the distance between data instances is meaningful in making predictions. As such, it often achieves very good performance.

When making predictions on regression problems, KNN will take the mean of the k most similar instances in the training dataset. Choose the KNN algorithm:

1. Click the “Choose” button and select “IBk” under the “lazy” group.
2. Click on the name of the algorithm to review the algorithm configuration.

In Weka KNN is called IBk which stands for Instance Based k.

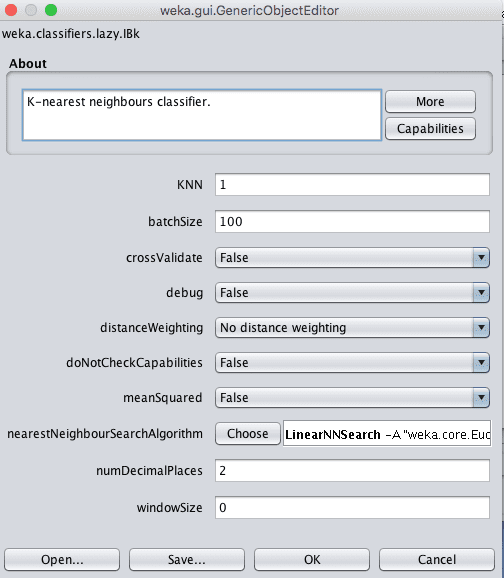
Weka k-Nearest Neighbors Configuration

The size of the neighborhood is controlled by the k parameter. For example, if set to 1, then predictions are made using the single most similar training instance to a given new pattern for which a prediction is requested. Common values for k are 3, 7, 11 and 21, larger for larger dataset sizes. Weka can automatically discover a good value for k using cross validation inside the algorithm by setting the crossValidate parameter to True.

Another important parameter is the distance measure used. This is configured in the nearestNeighbourSearchAlgorithm which controls the way in which the training data is stored and searched. The default is a LinearNNSearch. Clicking the name of this search algorithm will provide another configuration window where you can choose a distanceFunction parameter. By default, Euclidean distance is used to calculate the distance between instances, which is good for numerical data with the same scale. Manhattan distance is good to use if your attributes differ in measures or type.

It is a good idea to try a suite of different k values and distance measures on your problem and see what works best.

1. Click “OK” to close the algorithm configuration.
2. Click the “Start” button to run the algorithm on the Boston house price dataset.

You can see that with the default configuration that KNN algorithm achieves an RMSE of 4.6.

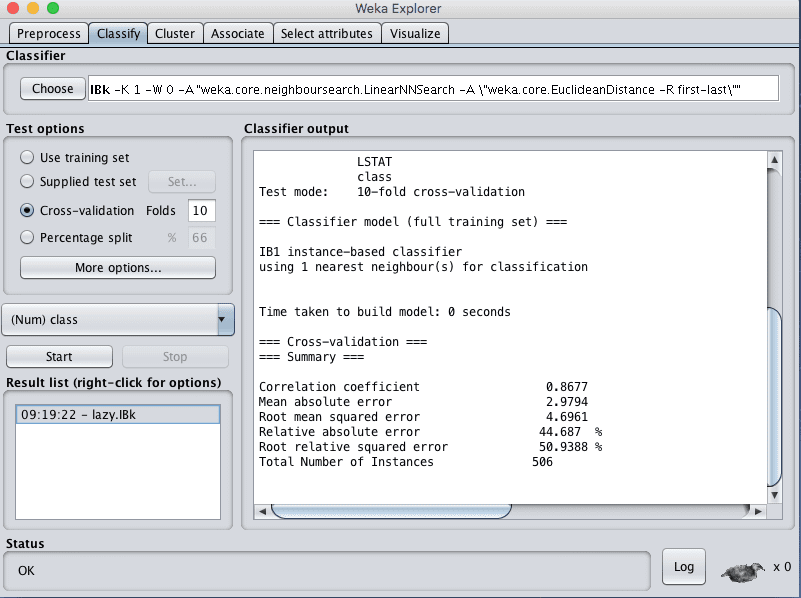
Weka Regression Results for the k-Nearest Neighbors Algorithm

Decision Tree

Decision trees can support classification and regression problems.

Decision trees are more recently referred to as Classification And Regression Trees or CART. They work by creating a tree to evaluate an instance of data, start at the root of the tree and moving town to the leaves (roots because the tree is drawn with an inverted prospective) until a prediction can be made. The process of creating a decision tree works by greedily selecting the best split point in order to make predictions and repeating the process until the tree is a fixed depth.

After the tree is construct, it is pruned in order to improve the model’s ability to generalize to new data.

Choose the decision tree algorithm:

1. Click the “Choose” button and select “REPTree” under the “trees” group.
2. Click on the name of the algorithm to review the algorithm configuration.

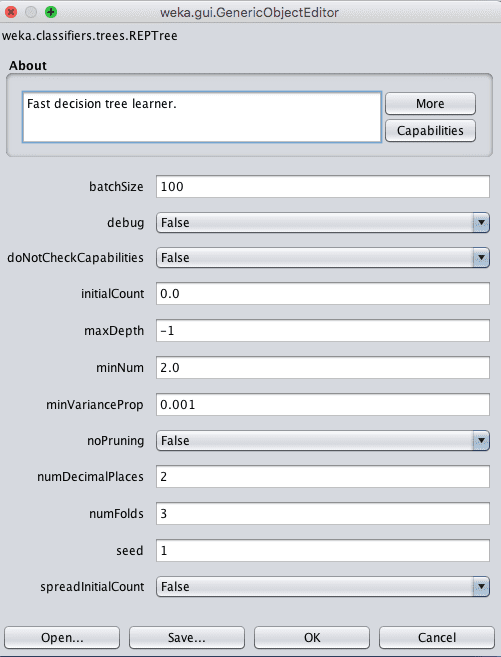
Weka Configuration for Decision Tree Algorithm

The depth of the tree is defined automatically, but can specify a depth in the maxDepth attribute.

You can also choose to turn off pruning by setting the noPruning parameter to True, although this may result in worse performance.

The minNum parameter defines the minimum number of instances supported by the tree in a leaf node when constructing the tree from the training data.

1. Click “OK” to close the algorithm configuration.
2. Click the “Start” button to run the algorithm on the Boston house price dataset.

You can see that with the default configuration that decision tree algorithm achieves an RMSE of 4.8.

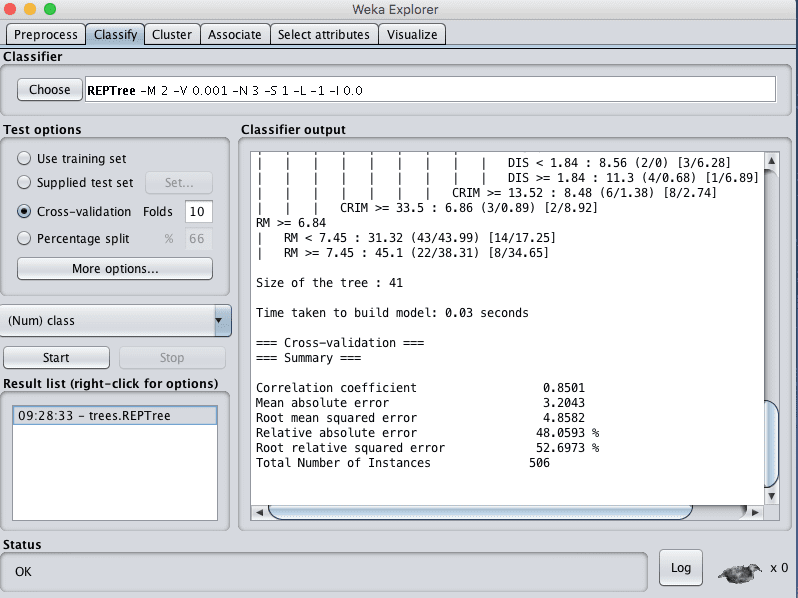
Weka Regression Results for the Decision Tree Algorithm

Support Vector Regression

Support Vector Machines were developed for binary classification problems, although extensions to the technique have been made to support multi-class classification and regression problems. The adaptation of SVM for regression is called Support Vector Regression or SVR for short.

SVM was developed for numerical input variables, although will automatically convert nominal values to numerical values. Input data is also normalized before being used.

Unlike SVM that finds a line that best separates the training data into classes, SVR works by finding a line of best fit that minimizes the error of a cost function. This is done using an optimization process that only considers those data instances in the training dataset that are closest to the line with the minimum cost. These instances are called support vectors, hence the name of the technique.

In almost all problems of interest, a line cannot be drawn to best fit the data, therefore a margin is added around the line to relax the constraint, allowing some bad predictions to be tolerated but allowing a better result overall.

Finally, few datasets can be fit with just a straight line. Sometimes a line with curves or even polygonal regions need to be marked out. This is achieved by projecting the data into a higher dimensional space in order to draw the lines and make predictions. Different kernels can be used to control the projection and the amount of flexibility.

Choose the SVR algorithm:

1. Click the “Choose” button and select “SMOreg” under the “function” group.
2. Click on the name of the algorithm to review the algorithm configuration.

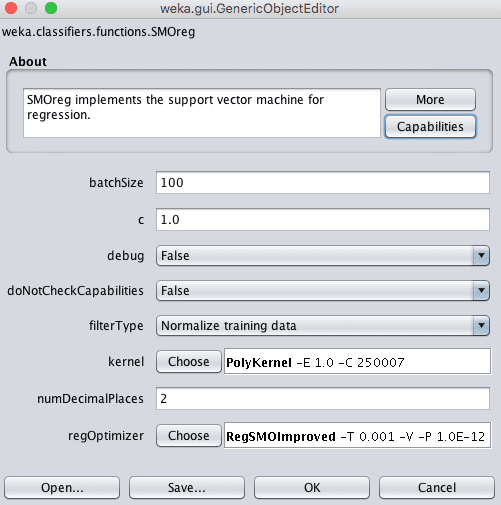
Weka Configuration for the Support Vector Regression Algorithm

The C parameter, called the complexity parameter in Weka controls how flexible the process for drawing the line to fit the data can be. A value of 0 allows no violations of the margin, whereas the default is 1.

A key parameter in SVM is the type of Kernel to use. The simplest kernel is a Linear kernel that separates data with a straight line or hyperplane. The default in Weka is a Polynomial Kernel that will fit the data using a curved or wiggly line, the higher the polynomial, the more wiggly (the exponent value).

The Polynomial Kernel has a default exponent of 1, which makes it equivalent to a linear kernel. A popular and powerful kernel is the RBF Kernel or Radial Basis Function Kernel that is capable of learning closed polygons and complex shapes to fit the training data.

It is a good idea to try a suite of different kernels and C (complexity) values on your problem and see what works best.

1. Click “OK” to close the algorithm configuration.
2. Click the “Start” button to run the algorithm on the Boston house price dataset.

You can see that with the default configuration that SVR algorithm achieves an RMSE of 5.1.

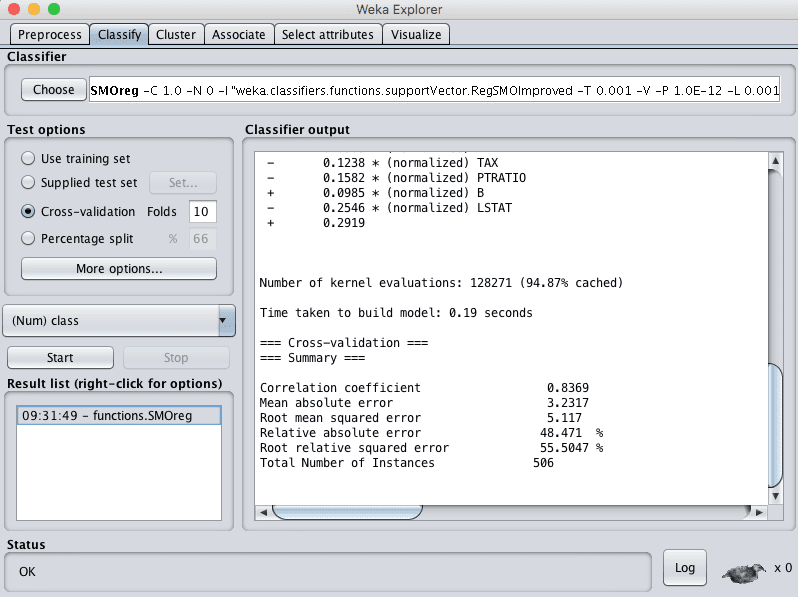
Weka Regression Results for the Support Vector Regression Algorithm

Multi-Layer Perceptron

The Multi-Layer Perceptron algorithms supports both regression and classification problems.

It is also called artificial neural networks or simply neural networks for short.

Neural networks are a complex algorithm to use for predictive modeling because there are so many configuration parameters that can only be tuned effectively through intuition and a lot of trial and error.

It is an algorithm inspired by a model of biological neural networks in the brain where small processing units called neurons are organized into layers that if configured well are capable of approximating any function. In classification we are interested in approximating the underlying function to best discriminate between classes. In regression problems we are interested in approximating a function that best fits the real value output.

Choose the Multi-Layer Perceptron algorithm:

1. Click the “Choose” button and select “MultilayerPerceptron” under the “function” group.
2. Click on the name of the algorithm to review the algorithm configuration.

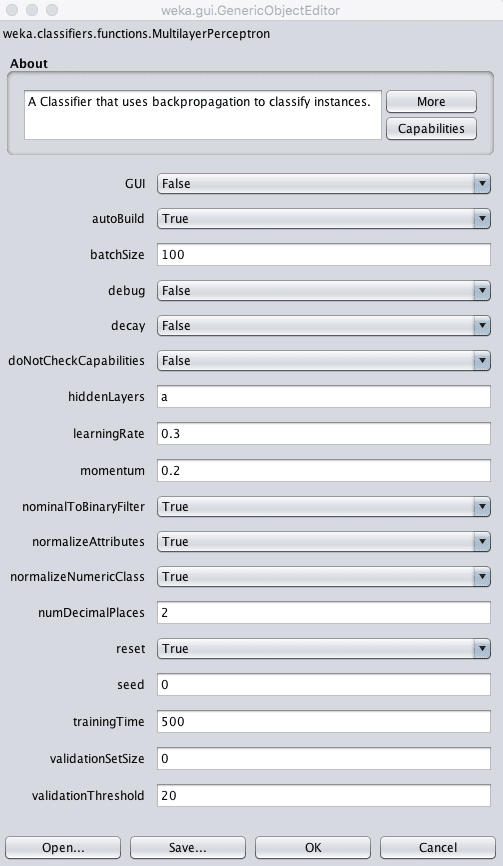
Weka Configuration for the Multi-Layer Perceptron Algorithm

You can manually specify the structure of the neural network that is used by the model, but this is not recommended for beginners.

The default will automatically design the network and train it on your dataset. The default will create a single hidden layer network. You can specify the number of hidden layers in the hiddenLayers parameter, set to automatic “a” by default.

You can also use a GUI to design the network structure. This can be fun, but it is recommended that you use the GUI with a simple train and test split of your training data, otherwise you will be asked to design a network for each of the 10 folds of cross validation.

Weka GUI Designer for the Multi-Layer Perceptron Algorithm

You can configure the learning process by specifying how much to update the model each epoch by setting the learning rate. common values are small such as values between 0.3 (the default) and 0.1.

The learning process can be further tuned with a momentum (set to 0.2 by default) to continue updating the weights even when no changes need to be made, and a decay (set decay to True) which will reduce the learning rate over time to perform more learning at the beginning of training and less at the end.

1. Click “OK” to close the algorithm configuration.
2. Click the “Start” button to run the algorithm on the Boston house price dataset.

You can see that with the default configuration that Multi-Layer Perceptron algorithm achieves an RMSE of 4.7.

Weka Regression Results Multi-Layer Perceptron Algorithm

Summary

In this post you discovered regression algorithms in Weka.

Specifically you learned:

• About 5 top regression algorithms you can use for predictive modeling.
• How to run regression algorithms in Weka.
• About key configuration options for regression algorithms in Weka.

Do you have any questions about regression algorithms in Weka or about this post? Ask your questions in the comments and I will do my best to answer.

Discover Machine Learning Without The Code!

Develop Your Own Models in Minutes

...with just a few a few clicks

Discover how in my new Ebook:
Machine Learning Mastery With Weka

Covers self-study tutorials and end-to-end projects like:
Loading data, visualization, build models, tuning, and much more...

Finally Bring The Machine Learning To Your Own Projects

Skip the Academics. Just Results.

See What's Inside