Long Short-Term Memory (LSTM) models are a type of recurrent neural network capable of learning sequences of observations.
This may make them a network well suited to time series forecasting.
An issue with LSTMs is that they can easily overfit training data, reducing their predictive skill.
Dropout is a regularization method where input and recurrent connections to LSTM units are probabilistically excluded from activation and weight updates while training a network. This has the effect of reducing overfitting and improving model performance.
In this tutorial, you will discover how to use dropout with LSTM networks and design experiments to test for its effectiveness for time series forecasting.
After completing this tutorial, you will know:
- How to design a robust test harness for evaluating LSTM networks for time series forecasting.
- How to design, execute, and interpret the results from using input weight dropout with LSTMs.
- How to design, execute, and interpret the results from using recurrent weight dropout with LSTMs.
Kick-start your project with my new book Deep Learning for Time Series Forecasting, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
- Updated Apr/2019: Updated the link to dataset.

How to Use Dropout with LSTM Networks for Time Series Forecasting
Photo by Jonas Bengtsson, some rights reserved.
Tutorial Overview
This tutorial is broken down into 5 parts. They are:
- Shampoo Sales Dataset
- Experimental Test Harness
- Input Dropout
- Recurrent Dropout
- Review of Results
Environment
This tutorial assumes you have a Python SciPy environment installed. You can use either Python 2 or 3 with this example.
This tutorial assumes you have Keras v2.0 or higher installed with either the TensorFlow or Theano backend.
This tutorial also assumes you have scikit-learn, Pandas, NumPy, and Matplotlib installed.
Next, let’s take a look at a standard time series forecasting problem that we can use as context for this experiment.
If you need help setting up your Python environment, see this post:
Need help with Deep Learning for Time Series?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Shampoo Sales Dataset
This dataset describes the monthly number of sales of shampoo over a 3-year period.
The units are a sales count and there are 36 observations. The original dataset is credited to Makridakis, Wheelwright, and Hyndman (1998).
The example below loads and creates a plot of the loaded dataset.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# load and plot dataset from pandas import read_csv from pandas import datetime from matplotlib import pyplot # load dataset def parser(x): return datetime.strptime('190'+x, '%Y-%m') series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser) # summarize first few rows print(series.head()) # line plot series.plot() pyplot.show() |
Running the example loads the dataset as a Pandas Series and prints the first 5 rows.
|
1 2 3 4 5 6 7 |
Month 1901-01-01 266.0 1901-02-01 145.9 1901-03-01 183.1 1901-04-01 119.3 1901-05-01 180.3 Name: Sales, dtype: float64 |
A line plot of the series is then created showing a clear increasing trend.
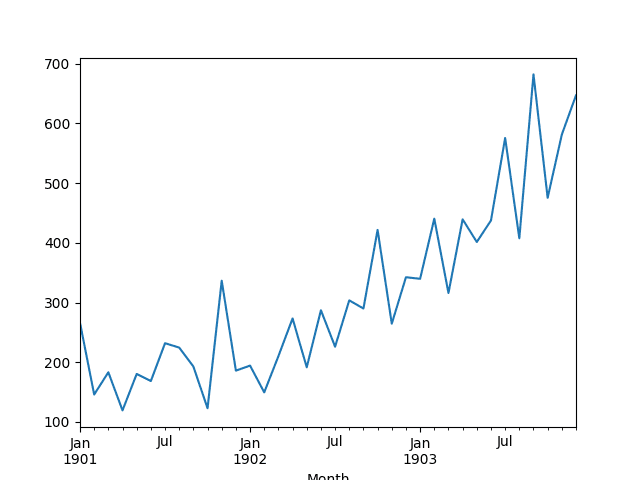
Line Plot of Shampoo Sales Dataset
Next, we will take a look at the model configuration and test harness used in the experiment.
Experimental Test Harness
This section describes the test harness used in this tutorial.
Data Split
We will split the Shampoo Sales dataset into two parts: a training and a test set.
The first two years of data will be taken for the training dataset and the remaining one year of data will be used for the test set.
Models will be developed using the training dataset and will make predictions on the test dataset.
The persistence forecast (naive forecast) on the test dataset achieves an error of 136.761 monthly shampoo sales. This provides a lower acceptable bound of performance on the test set.
Model Evaluation
A rolling-forecast scenario will be used, also called walk-forward model validation.
Each time step of the test dataset will be walked one at a time. A model will be used to make a forecast for the time step, then the actual expected value from the test set will be taken and made available to the model for the forecast on the next time step.
This mimics a real-world scenario where new Shampoo Sales observations would be available each month and used in the forecasting of the following month.
This will be simulated by the structure of the train and test datasets.
All forecasts on the test dataset will be collected and an error score calculated to summarize the skill of the model. The root mean squared error (RMSE) will be used as it punishes large errors and results in a score that is in the same units as the forecast data, namely monthly shampoo sales.
Data Preparation
Before we can fit a model to the dataset, we must transform the data.
The following three data transforms are performed on the dataset prior to fitting a model and making a forecast.
- Transform the time series data so that it is stationary. Specifically, a lag=1 differencing to remove the increasing trend in the data.
- Transform the time series into a supervised learning problem. Specifically, the organization of data into input and output patterns where the observation at the previous time step is used as an input to forecast the observation at the current time step
- Transform the observations to have a specific scale. Specifically, to rescale the data to values between -1 and 1.
These transforms are inverted on forecasts to return them into their original scale before calculating and error score.
LSTM Model
We will use a base stateful LSTM model with 1 neuron fit for 1000 epochs.
A batch size of 1 is required as we will be using walk-forward validation and making one-step forecasts for each of the final 12 months of test data.
A batch size of 1 means that the model will be fit using online training (as opposed to batch training or mini-batch training). As a result, it is expected that the model fit will have some variance.
Ideally, more training epochs would be used (such as 1500), but this was truncated to 1000 to keep run times reasonable.
The model will be fit using the efficient ADAM optimization algorithm and the mean squared error loss function.
Experimental Runs
Each experimental scenario will be run 30 times and the RMSE score on the test set will be recorded from the end each run.
Let’s dive into the experiments.
Baseline LSTM Model
Let’s start off with the baseline LSTM model.
The baseline LSTM model for this problem has the following configuration:
- Lag inputs: 1
- Epochs: 1000
- Units in LSTM hidden layer: 3
- Batch Size: 4
- Repeats: 3
The complete code listing is provided below.
This code listing will be used as the basis for all following experiments, with only the changes to this code listing provided in subsequent sections.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 |
from pandas import DataFrame from pandas import Series from pandas import concat from pandas import read_csv from pandas import datetime from sklearn.metrics import mean_squared_error from sklearn.preprocessing import MinMaxScaler from keras.models import Sequential from keras.layers import Dense from keras.layers import LSTM from math import sqrt import matplotlib # be able to save images on server matplotlib.use('Agg') from matplotlib import pyplot import numpy # date-time parsing function for loading the dataset def parser(x): return datetime.strptime('190'+x, '%Y-%m') # frame a sequence as a supervised learning problem def timeseries_to_supervised(data, lag=1): df = DataFrame(data) columns = [df.shift(i) for i in range(1, lag+1)] columns.append(df) df = concat(columns, axis=1) return df # create a differenced series def difference(dataset, interval=1): diff = list() for i in range(interval, len(dataset)): value = dataset[i] - dataset[i - interval] diff.append(value) return Series(diff) # invert differenced value def inverse_difference(history, yhat, interval=1): return yhat + history[-interval] # scale train and test data to [-1, 1] def scale(train, test): # fit scaler scaler = MinMaxScaler(feature_range=(-1, 1)) scaler = scaler.fit(train) # transform train train = train.reshape(train.shape[0], train.shape[1]) train_scaled = scaler.transform(train) # transform test test = test.reshape(test.shape[0], test.shape[1]) test_scaled = scaler.transform(test) return scaler, train_scaled, test_scaled # inverse scaling for a forecasted value def invert_scale(scaler, X, yhat): new_row = [x for x in X] + [yhat] array = numpy.array(new_row) array = array.reshape(1, len(array)) inverted = scaler.inverse_transform(array) return inverted[0, -1] # fit an LSTM network to training data def fit_lstm(train, n_batch, nb_epoch, n_neurons): X, y = train[:, 0:-1], train[:, -1] X = X.reshape(X.shape[0], 1, X.shape[1]) model = Sequential() model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True)) model.add(Dense(1)) model.compile(loss='mean_squared_error', optimizer='adam') for i in range(nb_epoch): model.fit(X, y, epochs=1, batch_size=n_batch, verbose=0, shuffle=False) model.reset_states() return model # run a repeated experiment def experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons): # transform data to be stationary raw_values = series.values diff_values = difference(raw_values, 1) # transform data to be supervised learning supervised = timeseries_to_supervised(diff_values, n_lag) supervised_values = supervised.values[n_lag:,:] # split data into train and test-sets train, test = supervised_values[0:-12], supervised_values[-12:] # transform the scale of the data scaler, train_scaled, test_scaled = scale(train, test) # run experiment error_scores = list() for r in range(n_repeats): # fit the model train_trimmed = train_scaled[2:, :] lstm_model = fit_lstm(train_trimmed, n_batch, n_epochs, n_neurons) # forecast test dataset test_reshaped = test_scaled[:,0:-1] test_reshaped = test_reshaped.reshape(len(test_reshaped), 1, 1) output = lstm_model.predict(test_reshaped, batch_size=n_batch) predictions = list() for i in range(len(output)): yhat = output[i,0] X = test_scaled[i, 0:-1] # invert scaling yhat = invert_scale(scaler, X, yhat) # invert differencing yhat = inverse_difference(raw_values, yhat, len(test_scaled)+1-i) # store forecast predictions.append(yhat) # report performance rmse = sqrt(mean_squared_error(raw_values[-12:], predictions)) print('%d) Test RMSE: %.3f' % (r+1, rmse)) error_scores.append(rmse) return error_scores # configure the experiment def run(): # load dataset series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser) # configure the experiment n_lag = 1 n_repeats = 30 n_epochs = 1000 n_batch = 4 n_neurons = 3 # run the experiment results = DataFrame() results['results'] = experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons) # summarize results print(results.describe()) # save boxplot results.boxplot() pyplot.savefig('experiment_baseline.png') # entry point run() |
Running the experiment prints summary statistics for the test RMSE for all repeats.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
We can see that on average this model configuration achieved a test RMSE of about 92 monthly shampoo sales with a standard deviation of 5.
|
1 2 3 4 5 6 7 8 9 |
results count 30.000000 mean 92.842537 std 5.748456 min 81.205979 25% 89.514367 50% 92.030003 75% 96.926145 max 105.247117 |
A box and whisker plot is also created from the distribution of test RMSE results and saved to a file.
The plot provides a clear depiction of the spread of the results, highlighting the middle 50% of values (the box) and the median (green line).
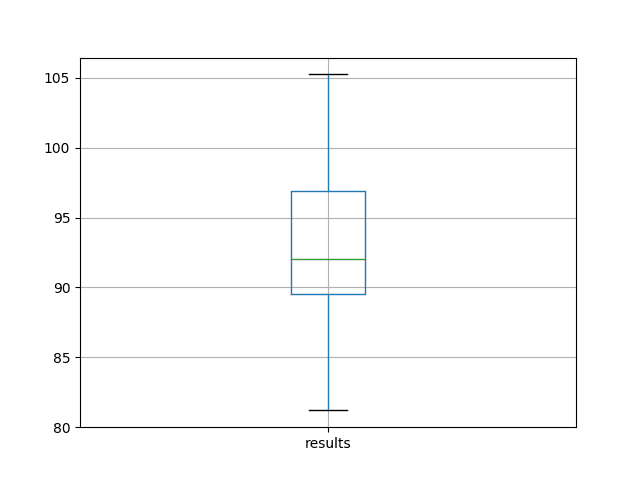
Box and Whisker Plot of Baseline Performance on the Shampoo Sales Dataset
Another angle to consider with a network configuration is how it behaves over time as the model is being fit.
We can evaluate the model on the training and test datasets after each training epoch to get an idea as to if the configuration is overfitting or underfitting the problem.
We will use this diagnostic approach on the top result from each set of experiments. A total of 10 repeats of the configuration will be run and the train and test RMSE scores after each training epoch plotted on a line plot.
In this case, we will use this diagnostic on the LSTM fit for 1000 epochs.
The complete diagnostic code listing is provided below.
As with the previous code listing, the code below will be used as the basis for all diagnostics in this tutorial and only the changes to this listing will be provided in subsequent sections.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 |
from pandas import DataFrame from pandas import Series from pandas import concat from pandas import read_csv from pandas import datetime from sklearn.metrics import mean_squared_error from sklearn.preprocessing import MinMaxScaler from keras.models import Sequential from keras.layers import Dense from keras.layers import LSTM from math import sqrt import matplotlib # be able to save images on server matplotlib.use('Agg') from matplotlib import pyplot import numpy # date-time parsing function for loading the dataset def parser(x): return datetime.strptime('190'+x, '%Y-%m') # frame a sequence as a supervised learning problem def timeseries_to_supervised(data, lag=1): df = DataFrame(data) columns = [df.shift(i) for i in range(1, lag+1)] columns.append(df) df = concat(columns, axis=1) return df # create a differenced series def difference(dataset, interval=1): diff = list() for i in range(interval, len(dataset)): value = dataset[i] - dataset[i - interval] diff.append(value) return Series(diff) # scale train and test data to [-1, 1] def scale(train, test): # fit scaler scaler = MinMaxScaler(feature_range=(-1, 1)) scaler = scaler.fit(train) # transform train train = train.reshape(train.shape[0], train.shape[1]) train_scaled = scaler.transform(train) # transform test test = test.reshape(test.shape[0], test.shape[1]) test_scaled = scaler.transform(test) return scaler, train_scaled, test_scaled # inverse scaling for a forecasted value def invert_scale(scaler, X, yhat): new_row = [x for x in X] + [yhat] array = numpy.array(new_row) array = array.reshape(1, len(array)) inverted = scaler.inverse_transform(array) return inverted[0, -1] # evaluate the model on a dataset, returns RMSE in transformed units def evaluate(model, raw_data, scaled_dataset, scaler, offset, batch_size): # separate X, y = scaled_dataset[:,0:-1], scaled_dataset[:,-1] # reshape reshaped = X.reshape(len(X), 1, 1) # forecast dataset output = model.predict(reshaped, batch_size=batch_size) # invert data transforms on forecast predictions = list() for i in range(len(output)): yhat = output[i,0] # invert scaling yhat = invert_scale(scaler, X[i], yhat) # invert differencing yhat = yhat + raw_data[i] # store forecast predictions.append(yhat) # report performance rmse = sqrt(mean_squared_error(raw_data[1:], predictions)) # reset model state model.reset_states() return rmse # fit an LSTM network to training data def fit_lstm(train, test, raw, scaler, batch_size, nb_epoch, neurons): X, y = train[:, 0:-1], train[:, -1] X = X.reshape(X.shape[0], 1, X.shape[1]) # prepare model model = Sequential() model.add(LSTM(neurons, batch_input_shape=(batch_size, X.shape[1], X.shape[2]), stateful=True)) model.add(Dense(1)) model.compile(loss='mean_squared_error', optimizer='adam') # fit model train_rmse, test_rmse = list(), list() for i in range(nb_epoch): model.fit(X, y, epochs=1, batch_size=batch_size, verbose=0, shuffle=False) model.reset_states() # evaluate model on train data raw_train = raw[-(len(train)+len(test)+1):-len(test)] train_rmse.append(evaluate(model, raw_train, train, scaler, 0, batch_size)) # evaluate model on test data raw_test = raw[-(len(test)+1):] test_rmse.append(evaluate(model, raw_test, test, scaler, 0, batch_size)) history = DataFrame() history['train'], history['test'] = train_rmse, test_rmse return history # run diagnostic experiments def run(): # config n_lag = 1 n_repeats = 10 n_epochs = 1000 n_batch = 4 n_neurons = 3 # load dataset series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser) # transform data to be stationary raw_values = series.values diff_values = difference(raw_values, 1) # transform data to be supervised learning supervised = timeseries_to_supervised(diff_values, n_lag) supervised_values = supervised.values[n_lag:,:] # split data into train and test-sets train, test = supervised_values[0:-12], supervised_values[-12:] # transform the scale of the data scaler, train_scaled, test_scaled = scale(train, test) # fit and evaluate model train_trimmed = train_scaled[2:, :] # run diagnostic tests for i in range(n_repeats): history = fit_lstm(train_trimmed, test_scaled, raw_values, scaler, n_batch, n_epochs, n_neurons) pyplot.plot(history['train'], color='blue') pyplot.plot(history['test'], color='orange') print('%d) TrainRMSE=%f, TestRMSE=%f' % (i+1, history['train'].iloc[-1], history['test'].iloc[-1])) pyplot.savefig('diagnostic_baseline.png') # entry point run() |
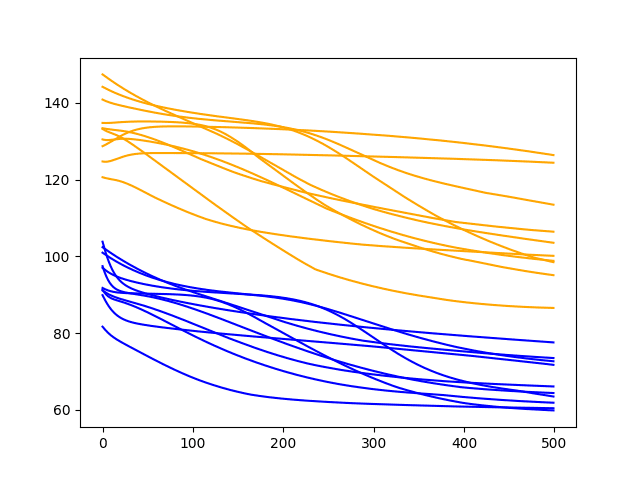
Running the diagnostic prints the final train and test RMSE for each run. More interesting is the final line plot created.
The line plot shows the train RMSE (blue) and test RMSE (orange) after each training epoch.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, the diagnostic plot shows a steady decrease in train and test RMSE to about 400-500 epochs, after which time it appears some overfitting may be occurring. This is signified by a continued decrease in train RMSE and an increase in test RMSE.
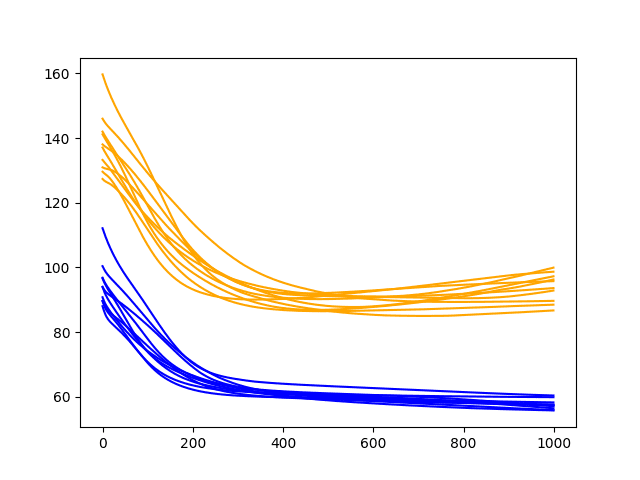
Diagnostic Line Plot of the Baseline Model on the Shampoo Sales Daset
Input Dropout
Dropout can be applied to the input connection within the LSTM nodes.
A dropout on the input means that for a given probability, the data on the input connection to each LSTM block will be excluded from node activation and weight updates.
In Keras, this is specified with a dropout argument when creating an LSTM layer. The dropout value is a percentage between 0 (no dropout) and 1 (no connection).
In this experiment, we will compare no dropout to input dropout rates of 20%, 40% and 60%.
Below lists the updated fit_lstm(), experiment(), and run() functions for using input dropout with LSTMs.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 |
# fit an LSTM network to training data def fit_lstm(train, n_batch, nb_epoch, n_neurons, dropout): X, y = train[:, 0:-1], train[:, -1] X = X.reshape(X.shape[0], 1, X.shape[1]) model = Sequential() model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True, dropout=dropout)) model.add(Dense(1)) model.compile(loss='mean_squared_error', optimizer='adam') for i in range(nb_epoch): model.fit(X, y, epochs=1, batch_size=n_batch, verbose=0, shuffle=False) model.reset_states() return model # run a repeated experiment def experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons, dropout): # transform data to be stationary raw_values = series.values diff_values = difference(raw_values, 1) # transform data to be supervised learning supervised = timeseries_to_supervised(diff_values, n_lag) supervised_values = supervised.values[n_lag:,:] # split data into train and test-sets train, test = supervised_values[0:-12], supervised_values[-12:] # transform the scale of the data scaler, train_scaled, test_scaled = scale(train, test) # run experiment error_scores = list() for r in range(n_repeats): # fit the model train_trimmed = train_scaled[2:, :] lstm_model = fit_lstm(train_trimmed, n_batch, n_epochs, n_neurons, dropout) # forecast test dataset test_reshaped = test_scaled[:,0:-1] test_reshaped = test_reshaped.reshape(len(test_reshaped), 1, 1) output = lstm_model.predict(test_reshaped, batch_size=n_batch) predictions = list() for i in range(len(output)): yhat = output[i,0] X = test_scaled[i, 0:-1] # invert scaling yhat = invert_scale(scaler, X, yhat) # invert differencing yhat = inverse_difference(raw_values, yhat, len(test_scaled)+1-i) # store forecast predictions.append(yhat) # report performance rmse = sqrt(mean_squared_error(raw_values[-12:], predictions)) print('%d) Test RMSE: %.3f' % (r+1, rmse)) error_scores.append(rmse) return error_scores # configure the experiment def run(): # load dataset series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser) # configure the experiment n_lag = 1 n_repeats = 30 n_epochs = 1000 n_batch = 4 n_neurons = 3 n_dropout = [0.0, 0.2, 0.4, 0.6] # run the experiment results = DataFrame() for dropout in n_dropout: results[str(dropout)] = experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons, dropout) # summarize results print(results.describe()) # save boxplot results.boxplot() pyplot.savefig('experiment_dropout_input.png') |
Running this experiment prints descriptives statistics for each evaluated configuration.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
The results suggest that on average an input dropout of 40% results in better performance, but the difference between the average result for a dropout of 20%, 40%, and 60% is very minor. All seemed to outperform no dropout.
|
1 2 3 4 5 6 7 8 9 |
0.0 0.2 0.4 0.6 count 30.000000 30.000000 30.000000 30.000000 mean 97.578280 89.448450 88.957421 89.810789 std 7.927639 5.807239 4.070037 3.467317 min 84.749785 81.315336 80.662878 84.300135 25% 92.520968 84.712064 85.885858 87.766818 50% 97.324110 88.109654 88.790068 89.585945 75% 101.258252 93.642621 91.515127 91.109452 max 123.578235 104.528209 96.687333 99.660331 |
A box and whisker plot is also created to compare the distributions of results for each configuration.
The plot shows the spread of results decreasing with the increase of input dropout. The plot also suggests that the input dropout of 20% may have a slightly lower median test RMSE.
The results do encourage the use of some input dropout for the chosen LSTM configuration, perhaps set to 40%.
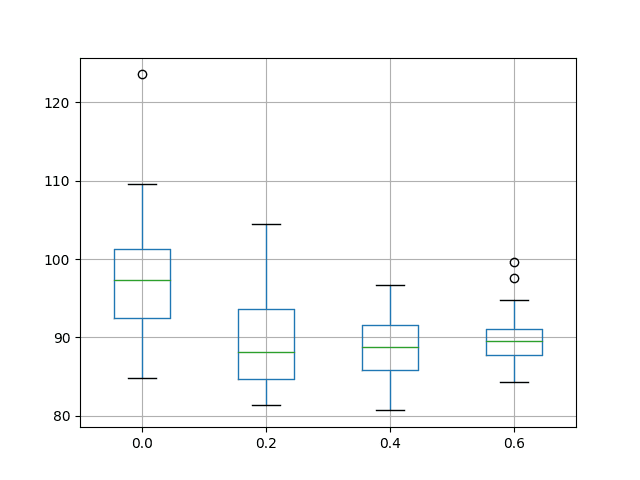
Box and Whisker Plot of Input Dropout Performance on the Shampoo Sales Dataset
We can review how input dropout of 40% affects the dynamics of the model while being fit to the training data.
The code below summarizes the updates to the fit_lstm() and run() functions compared to the baseline version of the diagnostic script.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
# fit an LSTM network to training data def fit_lstm(train, test, raw, scaler, batch_size, nb_epoch, neurons, dropout): X, y = train[:, 0:-1], train[:, -1] X = X.reshape(X.shape[0], 1, X.shape[1]) # prepare model model = Sequential() model.add(LSTM(neurons, batch_input_shape=(batch_size, X.shape[1], X.shape[2]), stateful=True, dropout=dropout)) model.add(Dense(1)) model.compile(loss='mean_squared_error', optimizer='adam') # fit model train_rmse, test_rmse = list(), list() for i in range(nb_epoch): model.fit(X, y, epochs=1, batch_size=batch_size, verbose=0, shuffle=False) model.reset_states() # evaluate model on train data raw_train = raw[-(len(train)+len(test)+1):-len(test)] train_rmse.append(evaluate(model, raw_train, train, scaler, 0, batch_size)) # evaluate model on test data raw_test = raw[-(len(test)+1):] test_rmse.append(evaluate(model, raw_test, test, scaler, 0, batch_size)) history = DataFrame() history['train'], history['test'] = train_rmse, test_rmse return history # run diagnostic experiments def run(): # config n_lag = 1 n_repeats = 10 n_epochs = 1000 n_batch = 4 n_neurons = 3 dropout = 0.4 # load dataset series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser) # transform data to be stationary raw_values = series.values diff_values = difference(raw_values, 1) # transform data to be supervised learning supervised = timeseries_to_supervised(diff_values, n_lag) supervised_values = supervised.values[n_lag:,:] # split data into train and test-sets train, test = supervised_values[0:-12], supervised_values[-12:] # transform the scale of the data scaler, train_scaled, test_scaled = scale(train, test) # fit and evaluate model train_trimmed = train_scaled[2:, :] # run diagnostic tests for i in range(n_repeats): history = fit_lstm(train_trimmed, test_scaled, raw_values, scaler, n_batch, n_epochs, n_neurons, dropout) pyplot.plot(history['train'], color='blue') pyplot.plot(history['test'], color='orange') print('%d) TrainRMSE=%f, TestRMSE=%f' % (i+1, history['train'].iloc[-1], history['test'].iloc[-1])) pyplot.savefig('diagnostic_dropout_input.png') |
Running the updated diagnostic creates a plot of the train and test RMSE performance of the model with input dropout after each training epoch.
The results show a clear addition of bumps to the train and test RMSE traces, which is more pronounced on the test RMSE scores.
We can also see that the symptoms of overfitting have been addressed with test RMSE continuing to go down over the entire 1000 epochs, perhaps suggesting the need for additional training epochs to capitalize on the behavior.
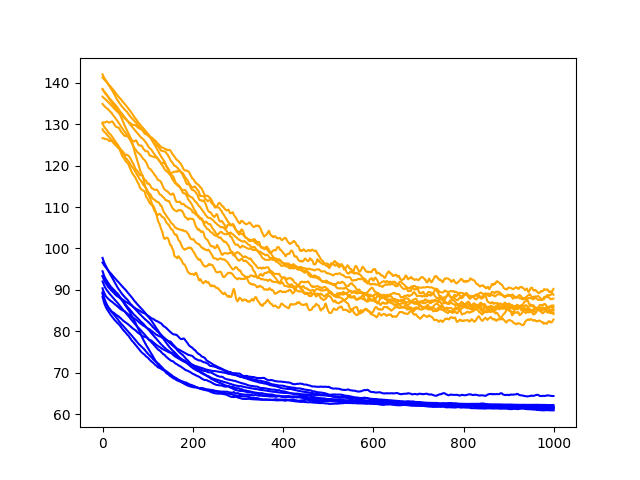
Diagnostic Line Plot of Input Dropout Performance on the Shampoo Sales Dataset
Recurrent Dropout
Dropout can also be applied to the recurrent input signal on the LSTM units.
In Keras, this is achieved by setting the recurrent_dropout argument when defining a LSTM layer.
In this experiment, we will compare no dropout to the recurrent dropout rates of 20%, 40%, and 60%.
Below lists the updated fit_lstm(), experiment(), and run() functions for using input dropout with LSTMs.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 |
# fit an LSTM network to training data def fit_lstm(train, n_batch, nb_epoch, n_neurons, dropout): X, y = train[:, 0:-1], train[:, -1] X = X.reshape(X.shape[0], 1, X.shape[1]) model = Sequential() model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True, recurrent_dropout=dropout)) model.add(Dense(1)) model.compile(loss='mean_squared_error', optimizer='adam') for i in range(nb_epoch): model.fit(X, y, epochs=1, batch_size=n_batch, verbose=0, shuffle=False) model.reset_states() return model # run a repeated experiment def experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons, dropout): # transform data to be stationary raw_values = series.values diff_values = difference(raw_values, 1) # transform data to be supervised learning supervised = timeseries_to_supervised(diff_values, n_lag) supervised_values = supervised.values[n_lag:,:] # split data into train and test-sets train, test = supervised_values[0:-12], supervised_values[-12:] # transform the scale of the data scaler, train_scaled, test_scaled = scale(train, test) # run experiment error_scores = list() for r in range(n_repeats): # fit the model train_trimmed = train_scaled[2:, :] lstm_model = fit_lstm(train_trimmed, n_batch, n_epochs, n_neurons, dropout) # forecast test dataset test_reshaped = test_scaled[:,0:-1] test_reshaped = test_reshaped.reshape(len(test_reshaped), 1, 1) output = lstm_model.predict(test_reshaped, batch_size=n_batch) predictions = list() for i in range(len(output)): yhat = output[i,0] X = test_scaled[i, 0:-1] # invert scaling yhat = invert_scale(scaler, X, yhat) # invert differencing yhat = inverse_difference(raw_values, yhat, len(test_scaled)+1-i) # store forecast predictions.append(yhat) # report performance rmse = sqrt(mean_squared_error(raw_values[-12:], predictions)) print('%d) Test RMSE: %.3f' % (r+1, rmse)) error_scores.append(rmse) return error_scores # configure the experiment def run(): # load dataset series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser) # configure the experiment n_lag = 1 n_repeats = 30 n_epochs = 1000 n_batch = 4 n_neurons = 3 n_dropout = [0.0, 0.2, 0.4, 0.6] # run the experiment results = DataFrame() for dropout in n_dropout: results[str(dropout)] = experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons, dropout) # summarize results print(results.describe()) # save boxplot results.boxplot() pyplot.savefig('experiment_dropout_recurrent.png') |
Running this experiment prints descriptive statistics for each evaluated configuration.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
The average results suggest that an average recurrent dropout of 20% or 40% is preferred, but overall the results are not much better than the baseline.
|
1 2 3 4 5 6 7 8 9 |
0.0 0.2 0.4 0.6 count 30.000000 30.000000 30.000000 30.000000 mean 95.743719 93.658016 93.706112 97.354599 std 9.222134 7.318882 5.591550 5.626212 min 80.144342 83.668154 84.585629 87.215540 25% 88.336066 87.071944 89.859503 93.940016 50% 96.703481 92.522428 92.698024 97.119864 75% 101.902782 100.554822 96.252689 100.915336 max 113.400863 106.222955 104.347850 114.160922 |
A box and whisker plot is also created to compare the distributions of results for each configuration.
The plot highlights the tighter distribution with a recurrent dropout of 40% compared to 20% and the baseline, perhaps making this configuration preferable. The plot also highlights that the min (best) test RMSE in the distribution appears to be have been affected when using recurrent dropout, providing worse performance.
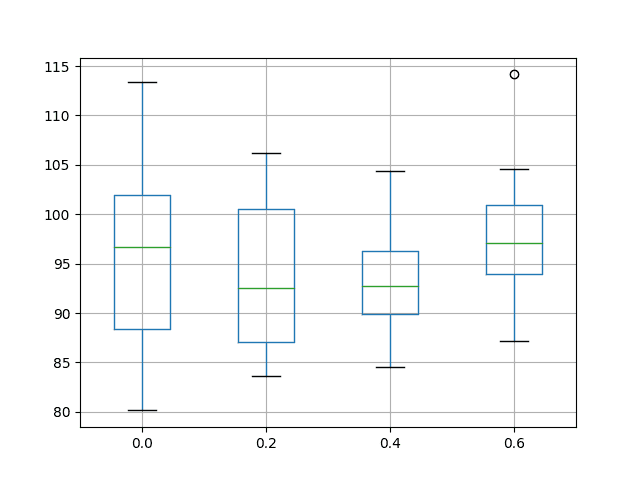
Box and Whisker Plot of Recurrent Dropout Performance on the Shampoo Sales Dataset
We can review how a recurrent dropout of 40% affects the dynamics of the model while being fit to the training data.
The code below summarizes the updates to the fit_lstm() and run() functions compared to the baseline version of the diagnostic script.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
# fit an LSTM network to training data def fit_lstm(train, test, raw, scaler, batch_size, nb_epoch, neurons, dropout): X, y = train[:, 0:-1], train[:, -1] X = X.reshape(X.shape[0], 1, X.shape[1]) # prepare model model = Sequential() model.add(LSTM(neurons, batch_input_shape=(batch_size, X.shape[1], X.shape[2]), stateful=True, recurrent_dropout=dropout)) model.add(Dense(1)) model.compile(loss='mean_squared_error', optimizer='adam') # fit model train_rmse, test_rmse = list(), list() for i in range(nb_epoch): model.fit(X, y, epochs=1, batch_size=batch_size, verbose=0, shuffle=False) model.reset_states() # evaluate model on train data raw_train = raw[-(len(train)+len(test)+1):-len(test)] train_rmse.append(evaluate(model, raw_train, train, scaler, 0, batch_size)) # evaluate model on test data raw_test = raw[-(len(test)+1):] test_rmse.append(evaluate(model, raw_test, test, scaler, 0, batch_size)) history = DataFrame() history['train'], history['test'] = train_rmse, test_rmse return history # run diagnostic experiments def run(): # config n_lag = 1 n_repeats = 10 n_epochs = 1000 n_batch = 4 n_neurons = 3 dropout = 0.4 # load dataset series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser) # transform data to be stationary raw_values = series.values diff_values = difference(raw_values, 1) # transform data to be supervised learning supervised = timeseries_to_supervised(diff_values, n_lag) supervised_values = supervised.values[n_lag:,:] # split data into train and test-sets train, test = supervised_values[0:-12], supervised_values[-12:] # transform the scale of the data scaler, train_scaled, test_scaled = scale(train, test) # fit and evaluate model train_trimmed = train_scaled[2:, :] # run diagnostic tests for i in range(n_repeats): history = fit_lstm(train_trimmed, test_scaled, raw_values, scaler, n_batch, n_epochs, n_neurons, dropout) pyplot.plot(history['train'], color='blue') pyplot.plot(history['test'], color='orange') print('%d) TrainRMSE=%f, TestRMSE=%f' % (i+1, history['train'].iloc[-1], history['test'].iloc[-1])) pyplot.savefig('diagnostic_dropout_recurrent.png') |
Running the updated diagnostic creates a plot of the train and test RMSE performance of the model with input dropout after each training epoch.
The plot shows the addition of bumps on the test RMSE traces, with little effect on the training RMSE traces. The plot also suggests a plateau, if not an increasing trend in test RMSE after about 500 epochs.
At least on this LSTM configuration and on this problem, perhaps recurrent dropout may not add much value.
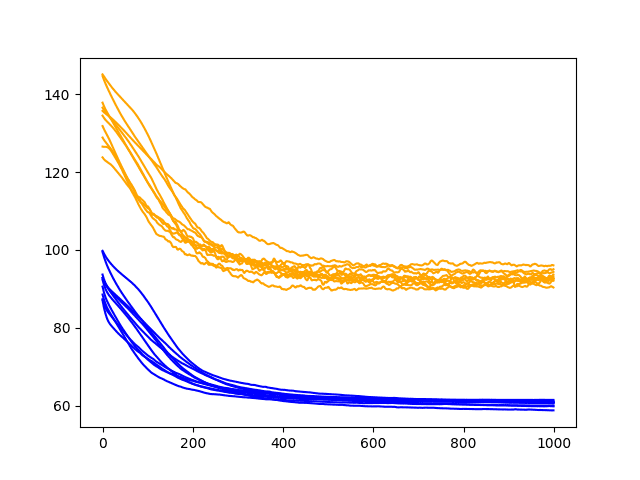
Diagnostic Line Plot of Recurrent Dropout Performance on the Shampoo Sales Dataset
Extensions
This section lists some ideas for further experiments you might like to consider exploring after completing this tutorial.
- Input Layer Dropout. It may be worth exploring the use of dropout on the input layer and how this impacts the performance and overfitting of the LSTM.
- Combine Input and Recurrent. It may be worth exploring the combination of both input and recurrent dropout to see if any additional benefit can be provided.
- Other Regularization Methods. It may be worth exploring other regularization methods with LSTM networks, such as various input, recurrent, and bias weight regularization functions.
Further Reading
For more on dropout with MLP models in Keras, see the post:
Below are some papers on dropout with LSTM networks that you might find useful for further reading.
- Recurrent Neural Network Regularization
- A Theoretically Grounded Application of Dropout in Recurrent Neural Networks
- Dropout improves Recurrent Neural Networks for Handwriting Recognition
Summary
In this tutorial, you discovered how to use dropout with LSTMs for time series forecasting.
Specifically, you learned:
- How to design a robust test harness for evaluating LSTM networks for time series forecasting.
- How to configure input weight dropout on LSTMs for time series forecasting.
- How to configure recurrent weight dropout on LSTMs for time series forecasting.
Do you have any questions about using dropout with LSTM networks?
Ask your questions in the comments below and I will do my best to answer.







Hi Jason,
I get an idea.
# transform data to be supervised learning
supervised = timeseries_to_supervised(diff_values, n_lag)
supervised_values = supervised.values[n_lag:,:]
# split data into train and test-sets
train, test = supervised_values[0:-12], supervised_values[-12:]
In fact, the first pair is: [ 0. -120.1]. what about throw away the first pair from the train data?
Starting from the true data instead of 0.
Hi Jason,
Are there plans to extend these tutorials to the multivariate case
Many thanks,
Best,
Andrew
Yes, there are a few scheduled on the blog in about a months time.
Any links?
I have a new book with many examples scheduled for one or two weeks from today.
Examples will also start appearing on the blog in coming weeks and continue all the way through to Christmas 2018.
Hi jason,
I would like to know how i can pass feature learnt from one deep learning model to another in keras. for instance, features learnt with Convolutional neural network to Recurrent neural network before making making prediction or classification results. This may involve using two deep learning model to develop projects.
Best
Henry
Yes, they are just weighted inputs (a functional transform of inputs).
Save the network and calculate the weighted output of inputs and use as inputs to another network.
On running program,
Error appeared
Using TensorFlow backend.
Traceback (most recent call last):
File “lstm_time_series_keras.py”, line 134, in
run()
File “lstm_time_series_keras.py”, line 126, in run
results[‘results’] = experiment(series, n_lag, n_repeats, n_epochs, n_batch, n_neurons)
File “lstm_time_series_keras.py”, line 93, in experiment
lstm_model = fit_lstm(train_trimmed, n_batch, n_epochs, n_neurons)
File “lstm_time_series_keras.py”, line 72, in fit_lstm
model.fit(X, y, epochs=1, batch_size=n_batch, verbose=0, shuffle=False)
File “/usr/local/lib/python2.7/dist-packages/keras/models.py”, line 870, in fit
initial_epoch=initial_epoch)
File “/usr/local/lib/python2.7/dist-packages/keras/engine/training.py”, line 1435, in fit
batch_size=batch_size)
File “/usr/local/lib/python2.7/dist-packages/keras/engine/training.py”, line 1333, in _standardize_user_data
str(x[0].shape[0]) + ‘ samples’)
ValueError: In a stateful network, you should only pass inputs with a number of samples that can be divided by the batch size. Found: 19 samples
Try changing the batch size to be divisible by the number of samples.
Hi Jason,
Great blog!
Can you share more on what’s the significants of the bumping RMSE plots? is it an acceptable condition, or we should try to fix it to make the RMSE plots smooth?
The smoothness is not really a concern. It is a result of the regularization of the network.
Hi Jason, thanks for the tutorials. What’s your opinion on recurrent dropout generally? I’ve seen a few sources saying it’s not a good idea.
e.g.
https://arxiv.org/pdf/1409.2329.pdf – “Standard dropout perturbs the recurrent connections, which makes it difficult for the LSTM to learn to store information for long periods of time. By not using dropout on the recurrent connections, the LSTM can benefit from dropout regularization without sacrificing its valuable memorization abilit”
I focus on the effect to model skill, I’ve found generally that dropout on input weights and weight regularization on inputs both result in better skill for simple sequence prediction tasks.
Hi Jason,
Thank you for your great article. I’m finding it very useful.
Just one question, in my case I’m scaling the input data between -1,1 but at the output of the model.predict() the data range is not not between -1 and 1. I have some strange values like -1.00688391 any idea?
thank you
The network may have a linear activation on the output layer. You could just round it.
Hey Jason,
why do you rescale the input to the range (-1, 1)?
By default the activation function of the LSTM is ‘linear’. Shouldn’t you have changed it to tanh?
The same question would easily apply to your post “How to Scale Data for Long Short-Term Memory Networks in Python”. In that post you rescale to (0,1). So in that case do you assume that the activation function is ‘sigmoid’?
Thanks in advance!
I should have normalized the data in [0,1], internal gates use sigmoid.
Hi Jason,
I was wondering Once the model is fitted on the training data and whenever i’m predicting on the test data, the output is different for the same set of test input. Why this is happening? and how can i make it static? Plz help!
Thanks.
Prakash
Neural networks are stochastic, this is a feature. See this post:
https://machinelearningmastery.com/randomness-in-machine-learning/
You can force them to be static, but you are fighting their nature:
https://machinelearningmastery.com/reproducible-results-neural-networks-keras/
Thanks. for the response. I figured it out it was because of we specified LSTM cell as state full. I was wondering, so right now we are predicting one step in time. How can i predict 30 steps ahead in time. I know one way could be predict for t+1 and use this predict for t+2. Is there any alternative. And if you can explain difference between lstm cell with state full and without state full? which one to use and when?
Waiting for your response.
Thanks.
Prakash Anand
See this post:
https://machinelearningmastery.com/multi-step-time-series-forecasting-long-short-term-memory-networks-python/
Could we create an ensemble of dropout models. And if yes then how can it be created.Ensemble could be of say N models where N can be an input parameter
Sure, you can create n models and combine their predictions. Dropout may or may not be used, it is an orthogonal concern.
Hey great article! Thank you.
Given limited dataset(time series data with length of a few thousands) do you think an RNN model will predict better if I create a batch with fixed size input sequence length(42) and fixed size output sequence length(7), or should I try batch with variable length in/output sequences?
Try it and see. Let me know how you go.
Hi Jason,
How can I modify this to include 25 features and predict sales for the next 2 steps based on the last 12 steps?
I’ve been following some of your other tutorials but I’m having trouble understanding the code needed to get the actual predictions out of the other end (into a plot etc). Can you point me in the right direction here too please?
As a side note, what would be my ‘sales’ data is either a 0 or a 1, so I am trying to predict whether the next 2 steps are 0’s or 1’s based on 25 features.
My df looks like this:
sales feature1 feature2 feature3 etc
date
This post has an example of a multi-step forecast:
https://machinelearningmastery.com/multi-step-time-series-forecasting-long-short-term-memory-networks-python/
This post has an example of multiple input features (multiple input series):
https://machinelearningmastery.com/multivariate-time-series-forecasting-lstms-keras/
Thanks Jason, very helpful to see how to implement dropout. However, I just got to say that this does not address overfitting as clearly the test error is much higher than the training error. Is there any other approaches to take here?
It will depend on your dataset and training configuration.
Hi Jason,
Thank you for this great post which helps me a lot!
However, I got an error of “IndexError: index 0 is out of bounds for axis 0 with size 0
” on series.plot() when run your code:
# load and plot dataset
from pandas import read_csv
from pandas import datetime
from matplotlib import pyplot
# load dataset
def parser(x):
return datetime.strptime(‘190’+x, ‘%Y-%m’)
series = read_csv(‘C:\\Users\\dell\\Anaconda3\\Input\\shampoosale.csv’, header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
# summarize first few rows
print(series.head())
# line plot
series.plot()
pyplot.show()
Thank you very much in advance!
Charles
Perhaps double check that you have loaded the data correctly?
Hi Jason,
Sorry to bother you again.
I can not see the box picture, and get the error message below when run the code of Baseline LSTM model:
C:\Users\dell\Anaconda3\lib\site-packages\ipykernel\__main__.py:133: FutureWarning:
The default value for ‘return_type’ will change to ‘axes’ in a future release.
To use the future behavior now, set return_type=’axes’.
To keep the previous behavior and silence this warning, set return_type=’dict’.
Thanks,
Charles
That looks like a warning that you could ignore.
Hey Jason!
Thanks for your awesome tutorials!
At the moment I am using an LSTM trying to predict cryptocurrency prices.
I am using your series to supervised function.
My setup:
583 days of training data and 146 of test.
Nuerons = 10
epochs = 100
batch size = 2
I am trying to predict one day ahead with t-1 as predictive variable. However I am overfitting quite a lot. Train RMSE of 1.98 vs Test RMSE of 11.55.
I have tried a lot of setups and even an altered version of your tuning tutorial.
Dropout does not improve my model (makes it worse)
Do you have any general ideas of how I could prevent overfitting or is this just an characteristic of this type of model and data?
Thanks!
Regularization and dropout are good approaches.
Perhaps early stopping, getting more data, using a larger learning rate, etc.
Any guidance in terms of how to properly use regular dropout with recurrent_dropout on time series? Seems some examples out there combine the two kinds of dropout, while yours is using just recurrent_dropout OR regular dropout. And there seems to be applying the dropout= parameter on a layer vs. a dropout layer by itself. What is the effective difference between these methods?
Good question.
I believe the nuance is the difference between dropout on the outputs of the layer vs dropout within the LSTM units themselves.
I don’t have more than that off the cuff, perhaps this paper one which the LSTM implementation is based will help:
http://arxiv.org/abs/1512.05287
Wish I were a little more nimble reading these kinds of papers, as I cannot make out if they combined traditional dropout and recurrent. I have found in my own experiments that a very small amount (5-10%) of traditional dropout combined with often high settings (50-80%) on recurrent dropout seems to do best.
Nice finding.
Hey Jason, I am trying to forecast a stationary time series data using lstm and facing the problem that var_loss keeps on inreasing and loss in decreasing for which I used dropout but still cannont make them converge ,please help
Perhaps try a model with a larger capacity (more layers or nodes) and a smaller learning rate?
Hey, Jason, you are a hero for machine learning education. I was working on computer security and started to learn machine learning for using in this field. I’m working on a model for recognizing malware binaries using convolutional layers and recurrent layers after that. I’m using dropout(0.15) after max-pooling layers and 0.4 after a dense layer after flatten output. Is it necessary for me to use dropout after recurrent layers (i’m experimenting on GRUs and LSTMs)? Thank you.
Nice work!
I recommend using whatever gives the best model performance.
Hi Jason,
I’m trying to apply variational dropout following ” http://arxiv.org/abs/1512.05287 ” paper. But I’m not sure if the recurrent_dropout in tensorflow uses different masks between the recurrent connections or not. I would appreciate if you could help me on that!
Not sure off the cuff, sorry.
Perhaps post to crossvalidated or the Keras user group?
Great help, especially the book!
When using the Theano backend in Keras, the
dropoutparameter to LSTM is no longer supported. Does it achieve the same effect to add a dropout layer ahead of the LSTM?No, it is different.
Hey Jason, thank you for the great article!
In the main text you write that a batch size of 1 is required as we will be using walk-forward validation and therefore the model will be fit using online training (as opposed to batch training or mini-batch training).
In the code you then use a batch size of 4. How is that possible? Are we still doing online training? Maybe the concept of batch for a stateful RNN is not clear to me. Could you please clarify? Thanks!
More generally, we can use any batch size we want with walk forward validation, learn more about the method here:
https://machinelearningmastery.com/backtest-machine-learning-models-time-series-forecasting/
Many thanks Jason for your informative post. I have a question. If I am using the LSTM network for direct forecasting (25 steps), and I use dropout layers at the same time, wouldn’t it cause a problem with the sequence of the data being predicted?
Hi Bita…I see no issue theoretically. Please proceed with your model and let us know your findings.