Keras uses fast symbolic mathematical libraries as a backend, such as TensorFlow and Theano.
A downside of using these libraries is that the shape and size of your data must be defined once up front and held constant regardless of whether you are training your network or making predictions.
On sequence prediction problems, it may be desirable to use a large batch size when training the network and a batch size of 1 when making predictions in order to predict the next step in the sequence.
In this tutorial, you will discover how you can address this problem and even use different batch sizes during training and predicting.
After completing this tutorial, you will know:
- How to design a simple sequence prediction problem and develop an LSTM to learn it.
- How to vary an LSTM configuration for online and batch-based learning and predicting.
- How to vary the batch size used for training from that used for predicting.
Kick-start your project with my new book Long Short-Term Memory Networks With Python, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.

How to use Different Batch Sizes for Training and Predicting in Python with Keras
Photo by steveandtwyla, some rights reserved.
Tutorial Overview
This tutorial is divided into 6 parts, as follows:
- On Batch Size
- Sequence Prediction Problem Description
- LSTM Model and Varied Batch Size
- Solution 1: Online Learning (Batch Size = 1)
- Solution 2: Batch Forecasting (Batch Size = N)
- Solution 3: Copy Weights
Tutorial Environment
A Python 2 or 3 environment is assumed to be installed and working.
This includes SciPy with NumPy and Pandas. Keras version 2.0 or higher must be installed with either the TensorFlow or Keras backend.
For help setting up your Python environment, see the post:
Need help with LSTMs for Sequence Prediction?
Take my free 7-day email course and discover 6 different LSTM architectures (with code).
Click to sign-up and also get a free PDF Ebook version of the course.
On Batch Size
A benefit of using Keras is that it is built on top of symbolic mathematical libraries such as TensorFlow and Theano for fast and efficient computation. This is needed with large neural networks.
A downside of using these efficient libraries is that you must define the scope of your data upfront and for all time. Specifically, the batch size.
The batch size limits the number of samples to be shown to the network before a weight update can be performed. This same limitation is then imposed when making predictions with the fit model.
Specifically, the batch size used when fitting your model controls how many predictions you must make at a time.
This is often not a problem when you want to make the same number predictions at a time as the batch size used during training.
This does become a problem when you wish to make fewer predictions than the batch size. For example, you may get the best results with a large batch size, but are required to make predictions for one observation at a time on something like a time series or sequence problem.
This is why it may be desirable to have a different batch size when fitting the network to training data than when making predictions on test data or new input data.
In this tutorial, we will explore different ways to solve this problem.
Sequence Prediction Problem Description
We will use a simple sequence prediction problem as the context to demonstrate solutions to varying the batch size between training and prediction.
A sequence prediction problem makes a good case for a varied batch size as you may want to have a batch size equal to the training dataset size (batch learning) during training and a batch size of 1 when making predictions for one-step outputs.
The sequence prediction problem involves learning to predict the next step in the following 10-step sequence:
|
1 |
[0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9] |
We can create this sequence in Python as follows:
|
1 2 3 |
length = 10 sequence = [i/float(length) for i in range(length)] print(sequence) |
Running the example prints our sequence:
|
1 |
[0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9] |
We must convert the sequence to a supervised learning problem. That means when 0.0 is shown as an input pattern, the network must learn to predict the next step as 0.1.
We can do this in Python using the Pandas shift() function as follows:
|
1 2 3 4 5 6 7 8 9 10 |
from pandas import concat from pandas import DataFrame # create sequence length = 10 sequence = [i/float(length) for i in range(length)] # create X/y pairs df = DataFrame(sequence) df = concat([df, df.shift(1)], axis=1) df.dropna(inplace=True) print(df) |
Running the example shows all input and output pairs.
|
1 2 3 4 5 6 7 8 9 |
1 0.1 0.0 2 0.2 0.1 3 0.3 0.2 4 0.4 0.3 5 0.5 0.4 6 0.6 0.5 7 0.7 0.6 8 0.8 0.7 9 0.9 0.8 |
We will be using a recurrent neural network called a long short-term memory network to learn the sequence. As such, we must transform the input patterns from a 2D array (1 column with 9 rows) to a 3D array comprised of [rows, timesteps, columns] where timesteps is 1 because we only have one timestep per observation on each row.
We can do this using the NumPy function reshape() as follows:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
from pandas import concat from pandas import DataFrame # create sequence length = 10 sequence = [i/float(length) for i in range(length)] # create X/y pairs df = DataFrame(sequence) df = concat([df, df.shift(1)], axis=1) df.dropna(inplace=True) # convert to LSTM friendly format values = df.values X, y = values[:, 0], values[:, 1] X = X.reshape(len(X), 1, 1) print(X.shape, y.shape) |
Running the example creates X and y arrays ready for use with an LSTM and prints their shape.
|
1 |
(9, 1, 1) (9,) |
LSTM Model and Varied Batch Size
In this section, we will design an LSTM network for the problem.
The training batch size will cover the entire training dataset (batch learning) and predictions will be made one at a time (one-step prediction). We will show that although the model learns the problem, that one-step predictions result in an error.
We will use an LSTM network fit for 1000 epochs.
The weights will be updated at the end of each training epoch (batch learning) meaning that the batch size will be equal to the number of training observations (9).
For these experiments, we will require fine-grained control over when the internal state of the LSTM is updated. Normally LSTM state is cleared at the end of each batch in Keras, but we can control it by making the LSTM stateful and calling model.reset_state() to manage this state manually. This will be needed in later sections.
The network has one input, a hidden layer with 10 units, and an output layer with 1 unit. The default tanh activation functions are used in the LSTM units and a linear activation function in the output layer.
A mean squared error optimization function is used for this regression problem with the efficient ADAM optimization algorithm.
The example below configures and creates the network.
|
1 2 3 4 5 6 7 8 9 |
# configure network n_batch = len(X) n_epoch = 1000 n_neurons = 10 # design network model = Sequential() model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True)) model.add(Dense(1)) model.compile(loss='mean_squared_error', optimizer='adam') |
We will fit the network to all of the examples each epoch and reset the state of the network at the end of each epoch manually.
|
1 2 3 4 |
# fit network for i in range(n_epoch): model.fit(X, y, epochs=1, batch_size=n_batch, verbose=1, shuffle=False) model.reset_states() |
Finally, we will forecast each step in the sequence one at a time.
This requires a batch size of 1, that is different to the batch size of 9 used to fit the network, and will result in an error when the example is run.
|
1 2 3 4 5 6 |
# online forecast for i in range(len(X)): testX, testy = X[i], y[i] testX = testX.reshape(1, 1, 1) yhat = model.predict(testX, batch_size=1) print('>Expected=%.1f, Predicted=%.1f' % (testy, yhat)) |
Below is the complete code example.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
from pandas import DataFrame from pandas import concat from keras.models import Sequential from keras.layers import Dense from keras.layers import LSTM # create sequence length = 10 sequence = [i/float(length) for i in range(length)] # create X/y pairs df = DataFrame(sequence) df = concat([df, df.shift(1)], axis=1) df.dropna(inplace=True) # convert to LSTM friendly format values = df.values X, y = values[:, 0], values[:, 1] X = X.reshape(len(X), 1, 1) # configure network n_batch = len(X) n_epoch = 1000 n_neurons = 10 # design network model = Sequential() model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True)) model.add(Dense(1)) model.compile(loss='mean_squared_error', optimizer='adam') # fit network for i in range(n_epoch): model.fit(X, y, epochs=1, batch_size=n_batch, verbose=1, shuffle=False) model.reset_states() # online forecast for i in range(len(X)): testX, testy = X[i], y[i] testX = testX.reshape(1, 1, 1) yhat = model.predict(testX, batch_size=1) print('>Expected=%.1f, Predicted=%.1f' % (testy, yhat)) |
Running the example fits the model fine and results in an error when making a prediction.
The error reported is as follows:
|
1 |
ValueError: Cannot feed value of shape (1, 1, 1) for Tensor 'lstm_1_input:0', which has shape '(9, 1, 1)' |
Solution 1: Online Learning (Batch Size = 1)
One solution to this problem is to fit the model using online learning.
This is where the batch size is set to a value of 1 and the network weights are updated after each training example.
This can have the effect of faster learning, but also adds instability to the learning process as the weights widely vary with each batch.
Nevertheless, this will allow us to make one-step forecasts on the problem. The only change required is setting n_batch to 1 as follows:
|
1 |
n_batch = 1 |
The complete code listing is provided below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
from pandas import DataFrame from pandas import concat from keras.models import Sequential from keras.layers import Dense from keras.layers import LSTM # create sequence length = 10 sequence = [i/float(length) for i in range(length)] # create X/y pairs df = DataFrame(sequence) df = concat([df, df.shift(1)], axis=1) df.dropna(inplace=True) # convert to LSTM friendly format values = df.values X, y = values[:, 0], values[:, 1] X = X.reshape(len(X), 1, 1) # configure network n_batch = 1 n_epoch = 1000 n_neurons = 10 # design network model = Sequential() model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True)) model.add(Dense(1)) model.compile(loss='mean_squared_error', optimizer='adam') # fit network for i in range(n_epoch): model.fit(X, y, epochs=1, batch_size=n_batch, verbose=1, shuffle=False) model.reset_states() # online forecast for i in range(len(X)): testX, testy = X[i], y[i] testX = testX.reshape(1, 1, 1) yhat = model.predict(testX, batch_size=1) print('>Expected=%.1f, Predicted=%.1f' % (testy, yhat)) |
Running the example prints the 9 expected outcomes and the correct predictions.
|
1 2 3 4 5 6 7 8 9 |
>Expected=0.0, Predicted=0.0 >Expected=0.1, Predicted=0.1 >Expected=0.2, Predicted=0.2 >Expected=0.3, Predicted=0.3 >Expected=0.4, Predicted=0.4 >Expected=0.5, Predicted=0.5 >Expected=0.6, Predicted=0.6 >Expected=0.7, Predicted=0.7 >Expected=0.8, Predicted=0.8 |
Solution 2: Batch Forecasting (Batch Size = N)
Another solution is to make all predictions at once in a batch.
This would mean that we could be very limited in the way the model is used.
We would have to use all predictions made at once, or only keep the first prediction and discard the rest.
We can adapt the example for batch forecasting by predicting with a batch size equal to the training batch size, then enumerating the batch of predictions, as follows:
|
1 2 3 4 |
# batch forecast yhat = model.predict(X, batch_size=n_batch) for i in range(len(y)): print('>Expected=%.1f, Predicted=%.1f' % (y[i], yhat[i])) |
The complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
from pandas import DataFrame from pandas import concat from keras.models import Sequential from keras.layers import Dense from keras.layers import LSTM # create sequence length = 10 sequence = [i/float(length) for i in range(length)] # create X/y pairs df = DataFrame(sequence) df = concat([df, df.shift(1)], axis=1) df.dropna(inplace=True) # convert to LSTM friendly format values = df.values X, y = values[:, 0], values[:, 1] X = X.reshape(len(X), 1, 1) # configure network n_batch = len(X) n_epoch = 1000 n_neurons = 10 # design network model = Sequential() model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True)) model.add(Dense(1)) model.compile(loss='mean_squared_error', optimizer='adam') # fit network for i in range(n_epoch): model.fit(X, y, epochs=1, batch_size=n_batch, verbose=1, shuffle=False) model.reset_states() # batch forecast yhat = model.predict(X, batch_size=n_batch) for i in range(len(y)): print('>Expected=%.1f, Predicted=%.1f' % (y[i], yhat[i])) |
Running the example prints the expected and correct predicted values.
|
1 2 3 4 5 6 7 8 9 |
>Expected=0.0, Predicted=0.0 >Expected=0.1, Predicted=0.1 >Expected=0.2, Predicted=0.2 >Expected=0.3, Predicted=0.3 >Expected=0.4, Predicted=0.4 >Expected=0.5, Predicted=0.5 >Expected=0.6, Predicted=0.6 >Expected=0.7, Predicted=0.7 >Expected=0.8, Predicted=0.8 |
Solution 3: Copy Weights
A better solution is to use different batch sizes for training and predicting.
The way to do this is to copy the weights from the fit network and to create a new network with the pre-trained weights.
We can do this easily enough using the get_weights() and set_weights() functions in the Keras API, as follows:
|
1 2 3 4 5 6 7 8 9 |
# re-define the batch size n_batch = 1 # re-define model new_model = Sequential() new_model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True)) new_model.add(Dense(1)) # copy weights old_weights = model.get_weights() new_model.set_weights(old_weights) |
This creates a new model that is compiled with a batch size of 1. We can then use this new model to make one-step predictions:
|
1 2 3 4 5 6 |
# online forecast for i in range(len(X)): testX, testy = X[i], y[i] testX = testX.reshape(1, 1, 1) yhat = new_model.predict(testX, batch_size=n_batch) print('>Expected=%.1f, Predicted=%.1f' % (testy, yhat)) |
The complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
from pandas import DataFrame from pandas import concat from keras.models import Sequential from keras.layers import Dense from keras.layers import LSTM # create sequence length = 10 sequence = [i/float(length) for i in range(length)] # create X/y pairs df = DataFrame(sequence) df = concat([df, df.shift(1)], axis=1) df.dropna(inplace=True) # convert to LSTM friendly format values = df.values X, y = values[:, 0], values[:, 1] X = X.reshape(len(X), 1, 1) # configure network n_batch = 3 n_epoch = 1000 n_neurons = 10 # design network model = Sequential() model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True)) model.add(Dense(1)) model.compile(loss='mean_squared_error', optimizer='adam') # fit network for i in range(n_epoch): model.fit(X, y, epochs=1, batch_size=n_batch, verbose=1, shuffle=False) model.reset_states() # re-define the batch size n_batch = 1 # re-define model new_model = Sequential() new_model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True)) new_model.add(Dense(1)) # copy weights old_weights = model.get_weights() new_model.set_weights(old_weights) # compile model new_model.compile(loss='mean_squared_error', optimizer='adam') # online forecast for i in range(len(X)): testX, testy = X[i], y[i] testX = testX.reshape(1, 1, 1) yhat = new_model.predict(testX, batch_size=n_batch) print('>Expected=%.1f, Predicted=%.1f' % (testy, yhat)) |
Running the example prints the expected, and again correctly predicted, values.
|
1 2 3 4 5 6 7 8 9 |
>Expected=0.0, Predicted=0.0 >Expected=0.1, Predicted=0.1 >Expected=0.2, Predicted=0.2 >Expected=0.3, Predicted=0.3 >Expected=0.4, Predicted=0.4 >Expected=0.5, Predicted=0.5 >Expected=0.6, Predicted=0.6 >Expected=0.7, Predicted=0.7 >Expected=0.8, Predicted=0.8 |
Summary
In this tutorial, you discovered how you can work around the need to vary the batch size used for training and prediction with the same network.
Specifically, you learned:
- How to design a simple sequence prediction problem and develop an LSTM to learn it.
- How to vary an LSTM configuration for online and batch-based learning and predicting.
- How to vary the batch size used for training from that used for predicting.
Do you have any questions about batch size?
Ask your questions in the comments below and I will do my best to answer.



Good tip. It is also useful to create another model just for evaluation of test dataset to compare RMSE between train/test.
What do you mean exactly Sam?
Hello Jason,
I have this data, where every 100 row represent a single class. How should I process the data for LSTM?
,emg1,emg2,emg3,emg4,emg5,emg6,emg7,emg8,quat1,quat2,quat3,quat4,acc1,acc2,acc3,gyro1,gyro2,gyro3
0,81,342,283,146,39,71,36,31,1121,-2490,930,16128,-797,4,2274,49,2920,252
0,70,323,259,125,34,53,29,31,1055,-3112,1075,16015,-878,369,1830,516,3590,243
0,53,298,246,100,49,37,27,33,1019,-3792,1239,15858,-809,527,1511,632,3953,46
0,42,154,193,172,95,48,28,28,1018,-4433,1360,15681,-724,358,1235,486,3754,-183
0,41,150,179,242,225,76,51,43,1066,-4980,1464,15503,-827,176,1073,525,3209,-415
…
Good question, this will give you ideas:
https://machinelearningmastery.com/faq/single-faq/what-is-the-difference-between-samples-timesteps-and-features-for-lstm-input
Hello, I would like to ask you how to multiply the weight of the current network by a parameter and assign it to another network, which is the so-called soft update. thank you very much
Could you explain the dimensions of the weight matrix for this model? Just curious and want to know. I am trying to understand how Keras stores weights.
You can print it out after compiling the model as follows:
Hello, could you explain why you redefine the n_batch = 1 to 1? I thought it should be a different value, no?
In which case Logan?
I think he means line 18 and 31 in the last complete example. Line 18 should be the following or ? n_batch=len(X)
Hi,Dr.Jason Brownlee .Could you tell me the keras version you use in this example,I try to copy the code to run in my mac,but it doesn’t work.
Keras version 2.0 or higher.
Hi, Jason Brownlee. Could you explain why you define the n_batch=1 in the line 18 of the last example? I think n_batch should be assigned with other values.
I have tried to redefine n_batch=len(X), train the model, and copy weights to the new model “new_model”. But I did get the right prediction result. Could you please help to find the reason?
>Expected=0.0, Predicted=0.0
>Expected=0.1, Predicted=0.1
>Expected=0.2, Predicted=0.3
>Expected=0.3, Predicted=0.5
>Expected=0.4, Predicted=0.8
>Expected=0.5, Predicted=1.1
>Expected=0.6, Predicted=1.4
>Expected=0.7, Predicted=1.7
>Expected=0.8, Predicted=2.1
The following is the code I used, which is same as the last example except the line 18
from pandas import DataFrame
from pandas import concat
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
# create sequence
length = 10
sequence = [i/float(length) for i in range(length)]
# create X/y pairs
df = DataFrame(sequence)
df = concat([df, df.shift(1)], axis=1)
df.dropna(inplace=True)
# convert to LSTM friendly format
values = df.values
X, y = values[:, 0], values[:, 1]
X = X.reshape(len(X), 1, 1)
# configure network
n_batch = len(X)
n_epoch = 1000
n_neurons = 10
# design network
model = Sequential()
model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True))
model.add(Dense(1))
model.compile(loss=’mean_squared_error’, optimizer=’adam’)
# fit network
for i in range(n_epoch):
model.fit(X, y, epochs=1, batch_size=n_batch, verbose=1, shuffle=False)
model.reset_states()
# re-define the batch size
n_batch = 1
# re-define model
new_model = Sequential()
new_model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True))
new_model.add(Dense(1))
# copy weights
old_weights = model.get_weights()
new_model.set_weights(old_weights)
# compile model
new_model.compile(loss=’mean_squared_error’, optimizer=’adam’)
# online forecast
for i in range(len(X)):
testX, testy = X[i], y[i]
testX = testX.reshape(1, 1, 1)
yhat = new_model.predict(testX, batch_size=n_batch)
print(‘>Expected=%.1f, Predicted=%.1f’ % (testy, yhat))
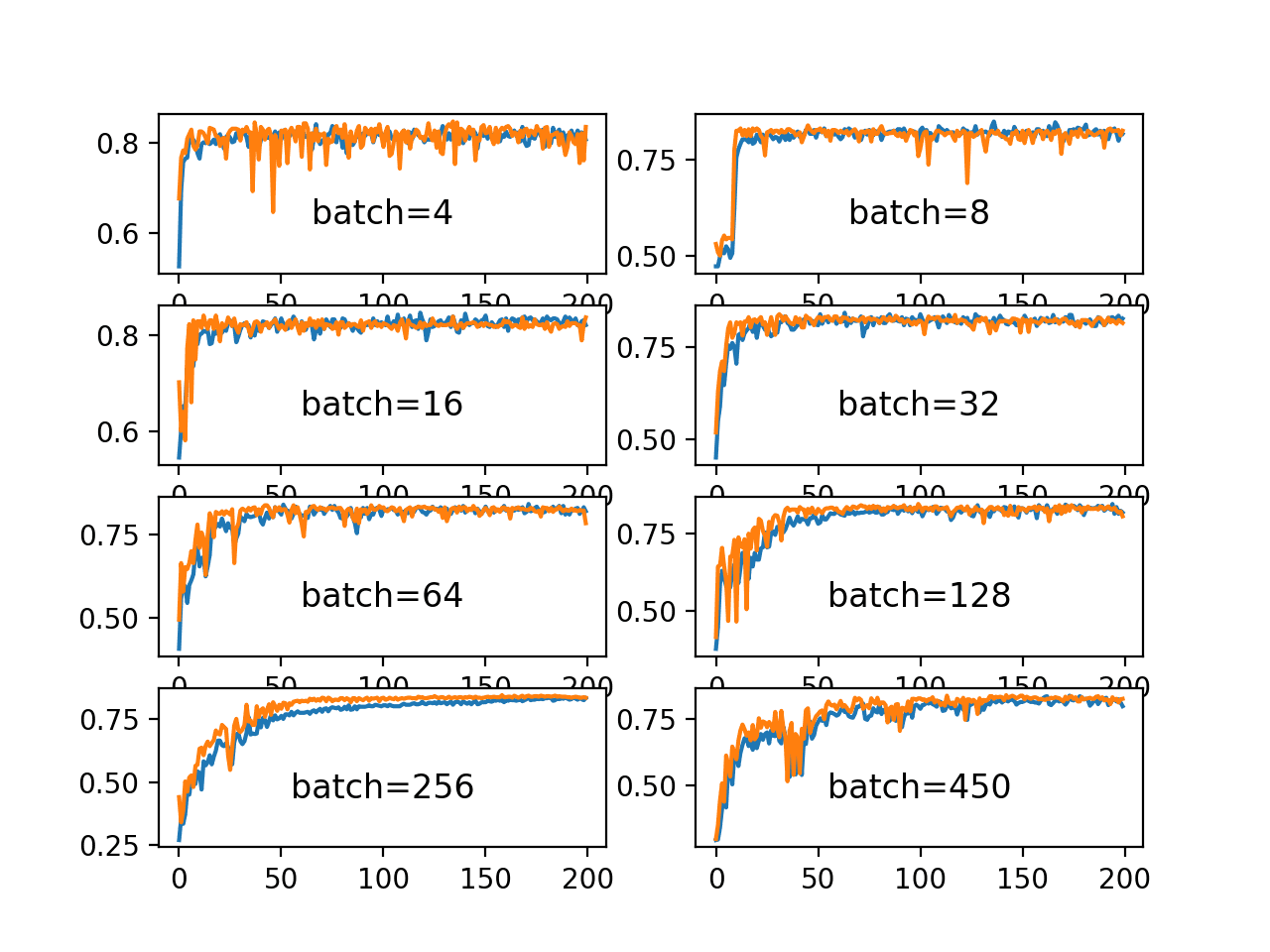
In testing I found that while a batch size of 1 looked like it was learning a pattern: http://tinyurl.com/ycutvy7h, a larger batch size often converges to a static prediction, much like linear regression (batch Size 5): http://tinyurl.com/yblzfus4
That said, the latter example (batch size 5) actually has a lower RMSE. It leaves me wondering if I actually have something learnable here, or if the flat line indicates no pattern beyond a regression?
Interesting.
Some problems may not benefit from a complex model like an LSTM. That is why we baseline using simple methods – to see if we can add value.
More complex/flexible is not always better.
Technically my problem might be a classification problem in that I really want to know, “Will tomorrow’s move be up or down?” Yet it’s not in the sense that magnitude matters. e.g. the following examples all have the same reward: a) correctly predicting an “up” tomorrow where truth was +6, b) predicting an “up” on 3 days where truth was +2, c) predicting “down” on two days that truth was -3.
Thoughts on the best model for that kind of problem? Considering reinforcement learning next, e.g. https://github.com/matthiasplappert/keras-rl.
Brainstorm all possible framings, then evaluate each.
I’ve seen extremely few examples of practitioners taking the DQN RL concept beyond Gym gaming examples. Do you see any reason why time series forecasting could not be looked at like an Atari game, where the observed game state is replaced with our time series observations and we ask the agent to forecast (play one of two paddle positions) for tomorrow being “up” or “down” as described above? Does that sound like an incremental advance beyond what we’re doing in your more regression-oriented approach taken in this post?
You could try it, I have not thought deeply about the suitability of DRL on time series sorry.
Very good post thank you Jason! I had this problem yesterday and your blog helped me solve it.
I think you should reset n_batch to a different value than 1 in the third solution as brought up by @Zhiyu Wang Because you redefine to 1 later in the code (line 31) so you didn’t end up having different batch size between training and predicting.
Thanks Saad, I see. I’ve updated the example to *actually* use different batch sizes in the final example!
Hello Dr. Brownlee, as someone that has recently started with Machine Learning I would like to thank you for all the great content. Your blog is extremely helpful.
As for the batches with different sizes – instead of providing “batch_input_shape” can’t we provide “input_shape” and then use “model.train_on_batch” and manually slice the inputs for each training step? We will also have to remove “stateful=True” but since the state is reset on each batch I believe it will still work the same. Something like this:
…
model.add(LSTM(n_neurons, input_shape=(X.shape[1], X.shape[2]))
…
for i in range(n_epoch):
batch_start = 0
for j in range(1, len(X) + 1):
if j % n_batch == 0:
model.train_on_batch(X[batch_start:j], y[batch_start:j])
batch_start = j
I guess I was focused on showing how to do this when the LSTM is stateful.
The risk is that you will cut down on sequence length, and impact BPTT.
With everything, test and see how it fairs on your problem.
Hi Jason,
I was having trouble with model.predict() in my stateful LSTM, and I finally got it to work thanks to what I learned from this page, thank you!
However I’m still confused by one thing.
In the intro at the top of the page, it says that when using Keras, “you must define the scope of your data upfront and for all time. Specifically, the batch size.”
That seems to be true for stateful LSTM’s, not true for stateless LSTM’s, and I dunno about other RNN’s or the rest of Keras. Perhaps you could clarify.
The reason I doubt it for stateless LSTM’s is that the example at
https://github.com/fchollet/keras/blob/master/examples/lstm_text_generation.py
works fine. The gist of it:
model = Sequential()
model.add(LSTM(128, input_shape=(maxlen, len(chars))))
model.add(Dense(len(chars)))
model.add(Activation(‘softmax’))
model.fit(X, y, batch_size=128, epochs=1)
x = np.zeros((1, maxlen, len(chars)))
for t, char in enumerate(sentence):
x[0, t, char_indices[char]] = 1.
preds = model.predict(x, verbose=0)[0]
So it specifies nothing about batch size when constructing the model; it trains it with an explicit batch size argument of 128; and it calls predict() without any batch size argument on a dataset whose batch size is 1. It seems like the model has not bound the batch size, and adapts dynamically to whatever data you give it.
But I spent a lot of time trying to modify that example to work with a stateful LSTM, and failed. Evidently you are correct that for stateful LSTM’s, one cannot do that. One has to specify the batch size explicitly to add a stateful LSTM layer to the model, and after that the model is rigidly bound to that size and can neither train nor predict on data of any other batch size.
Correct me if I’m wrong, I’m new at this.
Thanks!
Yes, this is correct for stateful LSTMs only.
Hi Jason,
Thanks for the great tutorial.
The batch size limits the number of samples to be shown to the network before a weight update can be performed.
“””””””””This same limitation is then imposed when making predictions with the fit model.
Specifically, the batch size used when fitting your model controls how many predictions you must make at a time.”””””””
can you please elaborate how batch size affects the prediction?
Yes, what is the problem exactly?
thanx alot for your tutorial. its very helpful.
can you please help me with my problem
i used your solution 3 i.e copied weights from trained model to new one
but still while predicting with single batch test data i get same error i.e:
“AttributeError: ‘list’ object has no attribute ‘shape'”
my data:
training input data has shape(5,2,3)
test input data shape(1,2,3)
training output data shape(5,2,5)
expected output data shape(1,2,5)
code:
model = Sequential()
model.add(LSTM(5, batch_input_shape=(5, 2, 3), unroll=True, return_sequences=True))
model.add(Dense(5))
model.compile(loss=’mean_absolute_error’, optimizer=’adam’)
model.fit(x, o, nb_epoch=2000, batch_size=5, verbose=2)
new_model = Sequential()
new_model.add(LSTM(5, batch_input_shape=(1, 2, 3), unroll=True, return_sequences=True))
new_model.add(Dense(5))
old_weights = model.get_weights()
new_model.set_weights(old_weights)
new_model.compile(loss=’mean_absolute_error’, optimizer=’adam’)
thanx alot in advance
Glad to hear it.
The error suggests perhaps the input data is a list rather than a numpy array. Try converting it to a numpy array.
I tried using the third method, saving the weights of the model then defining a new model with batch size equal one. However, when I run the new model on the same data set, I find that I’m getting different results for a lot of the results except the 1st prediction. If I train a model with batch size = 1, then creating a new model with the old model’s weights gives identical predictions. Does a model with different batch size treat the data in a fundamentally different way? Like if my batch size = 32, do predictions 1-32, 33-64, 65-96… predict using the one state for each group, while a model with batch size 1 updates the state for each and every input?
THe batch size could impact the training, it controls the number of samples to use to estimate the error gradient before an update.
Perhaps that is what is going on in your case. Perhaps test with different batch sizes to see how sensitive your model is to the value?
I’m seeing similar results. If I train on one batch size and copy the weights to a model with a different batch size, the new model’s prediction error is always worse.
I decided to simplify my dataset. Now I’m working with 50 cosine periods with 1000 points per a period and I’m predicting the next point in the series from the current point. Simplifying the dataset didn’t give me any better results.
I’ve tried an assortment of batch sizes for the model that I train with and the model that I copy the weights to. The batch sizes don’t seem to make much of a difference.
The good news is that copying the weights into a model with the same batch size doesn’t change anything, so I know I’m doing the copying correctly.
It may be the stochastic nature of the neural net.
Ensure you have a robust evaluation of your model first. I recommend this procedure:
https://machinelearningmastery.com/evaluate-skill-deep-learning-models/
Thank you for the lead. It was a big help.
The model with the copied weights still performs worse, and I have better metrics to prove it.
The good news is that I’ve also improved the model that comes out of the training, and that improvement shows up in the model with copied weights.
Since I’m training on sequential data, I don’t allow it to be shuffled and I wasn’t shuffling it between epochs. Each epoch was just trained on the same sequence of data as the previous epoch.
Your section on k-fold cross validation led me to try something similar that preserves the data sequence. Now I shift the start of the sequence between epochs and end up with a set of weights that seem to transfer better.
Nice one, thanks for letting me know Michael.
Hi Jason, I copy and paste to run the last example in my local, but the output is not the same with yours.
keras version: 2.0.8
>Expected=0.0, Predicted=0.0
>Expected=0.1, Predicted=0.1
>Expected=0.2, Predicted=0.3
>Expected=0.3, Predicted=0.5
>Expected=0.4, Predicted=0.6
>Expected=0.5, Predicted=0.7
>Expected=0.6, Predicted=0.8
>Expected=0.7, Predicted=0.9
>Expected=0.8, Predicted=0.9
Perhaps try and run the example a few times?
I was having similar problems with my predictions being off. Everything started working when I made the new model non stateful. My next piece of homework is figure out why. My running theory is that the state is defined to work on 9 data samples at a time, and not 1.
I will experiment with a few different training and prediction batch sizes to see if the predictions with a stateful model converge.
Hang in there.
I have the same issue, with
new_model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True))
I get:
>Expected=0.0, Predicted=0.0
>Expected=0.1, Predicted=0.1
>Expected=0.2, Predicted=0.3
>Expected=0.3, Predicted=0.5
>Expected=0.4, Predicted=0.7
>Expected=0.5, Predicted=1.0
>Expected=0.6, Predicted=1.3
>Expected=0.7, Predicted=1.6
>Expected=0.8, Predicted=1.8
with
new_model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=False))
I get:
>Expected=0.0, Predicted=0.0
>Expected=0.1, Predicted=0.1
>Expected=0.2, Predicted=0.2
>Expected=0.3, Predicted=0.3
>Expected=0.4, Predicted=0.4
>Expected=0.5, Predicted=0.5
>Expected=0.6, Predicted=0.6
>Expected=0.7, Predicted=0.7
>Expected=0.8, Predicted=0.8
As the original model was stateful, shouldn’t the new one be stateful too?
Hi Jason!
I think here you should change the DataFrame shifting from:
# create X/y pairs
df = DataFrame(sequence)
df = concat([df, df.shift(1)], axis=1)
to:
# create X/y pairs
df = DataFrame(sequence)
df = concat([df, df.shift(-1)], axis=1)
To get the training/test sets in different order:
1 0.0 0.1
2 0.1 0.2
3 0.2 0.3
4 0.3 0.4
5 0.4 0.5
6 0.6 0.7
7 0.7 0.8
8 0.8 0.9
9 0.9 NA ????
Or did i miss something?
I agree – confused me to start with!
Hey Jason,
I have a question for you and would love your insight.
I am building a model, a stacked LSTM model with return sequences = True, stateful = True, with a TimeDistributed dense layer.
in essence, i am confused with the following.
imagine my dataset is X = [0,1,2,3,4,5], and Y = [7,8,9,10,11,12], and I am training with a batch_size = 2
So i transform X to look like [[[0],[3]], [[1],[4]], [[2],[5]]], that is, 3 batches feeding 2 timestamps containing one feature each.
I also make the assumption that I need to transform Y as well to [[[7],[10]], [[8],[11]], [[9],[12]]].
Is this correct? And if it is, does that imply that I need to reorder my output upon receiving a prediction?
And how does that change when I change the prediction size of the batch to 1?
Oops sorry, I meant to say dataset = [1,2,3,4,5,6,7,8,9,10]
and I want my input sequence to be [1,2] and my model to return the output sequence [3,4]
with a batch size = 2, what would my input/output look like?
How would this differ when i change the batch size = 1?
This post will help you reshape your dataset:
https://machinelearningmastery.com/reshape-input-data-long-short-term-memory-networks-keras/
Hi,
Thanks a lot for the tutorial. As a beginner, I learn a lot, but I get in trouble with understanding the concept of batch size and time step in stateful lstm.
From keras document, “stateful: Boolean (default False). If True, the last state for each sample at index i in a batch will be used as initial state for the sample of index i in the following batch.” It seems to be different from solutioin 2 & solution 3.
For example, consider 4 sequences as x,
[1,2,3,4]
[a,b,c,d]
[5,6,7,8]
[e,f,g,h]
When batch size != 1, how to construct x?
when timesteps = 1,
from document, x seems to be [[1,a,5,e],[2,b,6,f],[3,c,7,g],[4,d,8,h]]
from your tutorial, x seems to be [[1,2,3,4],[a,b,c,d],[5,6,7,8],[e,f,g,h]]
which one is right?
The construction of your input samples is not effected by your batch size.
I’m not sure if my current method accomplishes the same thing.
I have a training process where at the end of it, it saves the model and the weights to a file.
model.save(model_file)
model.save_weights(weights_file)
Then a prediction routine loads them using:
model = load_model(model_file)
model.load_weights(weights_file)
The prediction routine does not rebuild the network in code, just from the file.
Then I use the:
raw_prediction = model.predict(x_scaled, batch_size=1)
Is there anything that I should be doing that I’m not? Your code has stateful LSTMs, and rebuilds the network from scratch and I don’t know if those steps end up causing any different results.
I’m also very unclear about the reasoning behind running .fit() on the same set of data multiple times.
# fit network
for i in range(n_epoch):
model.fit(X, y, epochs=1, batch_size=n_batch, verbose=1, shuffle=False)
model.reset_states()
What does that provide?
It shows how to run training epochs manually across all samples in the training dataset, giving you the control to reset state between epochs.
Thanks for the tutorial, I had a question regarding the stateful RNNs/LSTMs.
The Kerras documentation here https://keras.io/getting-started/faq/ states that
Making a RNN stateful means that the states for the samples of each batch will be reused as initial states for the samples in the next batch.When using stateful RNNs, it is therefore assumed that:
all batches have the same number of samples
If x1 and x2 are successive batches of samples, then x2[i] is the follow-up sequence to x1[i], for every i.
If this is correct then it means if I have m independently measured time series (lets say m observations of the same phenomenon from a different source) consisting each of n points. Each of these point is a scalar (for the sake of simplicity).
1) Then for stateful RNNs in total I need to have n batches.
2) Each batch would be of dimension (m,1) and consists of ith sample of each time series where
i<=n.
3) The batches need to be ordered 1 to n
In lay man terms, each batch would contain ith sample from each time series. horizontal slicing to get batches.
Is my understanding correct?
PS. The effect of converting each time series to a supervised time series is not taken into consideration here.
Sounds correct.
In your first example where n_batch = len(X), would it be the same if you had just set Stateful = False and not reset_states after each epoch?
All samples in one batch preserves state and does one weight update at the end.
Hi, great tutorials. I’ve learned a lot. I just have one question. With this I could train my lstm on a 3 year data set, then save the weights, and make a new lstm net load the weigths and train it with each new observation that comes in and forecast 1 observatiion ahead??
What i’m looking for is to avoid keeping the 3 years history after the training step, and just retrain the net with the new data.
Thank you!
Yes, this is called model updating. See this post:
https://machinelearningmastery.com/update-lstm-networks-training-time-series-forecasting/
Great! Thank you Jason, great articles!
Thanks.
Hi,
I’m hard time finding the reason, why input structure in RNN for character and time-series analysis is different. E.g.
for character analysis, we use input structure the following:
input = tf.placeholder(tf.int32, [batch_size, num_steps], name = "input"]But for time-series analysis, it’s the following:
input = tf.placeholder(tf.int32, [batch_size,time_steps, inputs], name = "input"]Assuming,
num_stepandtime_stepsare the same (number of period the RNN is looking back into past), why additionalinputsis used in time-series analysis of RNN?If someone please help me answer this question, I’ll be extremely grateful! I’m having extremely hard time grasping this issue.
Thanks!
Sorry, I don’t have any direct examples in tensorflow.
Hi Dr. Jason,
I am using keras 2.1.2 and I was looking at your example.
I was wondering why do I need to build an entire new network to use different batch size when we already have an option to pass batch_size to the model.predict method.
If can simply use:
model.fit(….batch_size=n1)
and then
model.predict(….batch_size=n2)
Am I missing the entire intuition behind this article?
If that is the case then I am apologizing in advance.
Kind Regards,
Mohaimen
Because it will fail with an error.
Hi Dr. Jason,
Thanks a lot for your reply.
I looked at the model.predict documentation. It says if you do not pass a batch size here, it uses the default batch size which is 32. I have tested it and it does not fail.
Probably I am missing something. I will look at it again and if I find it failing, I will comeback and let you know.
BTW, is there a way to do distributed model training in keras except using elephas and dist-keras? It seems that elephas is broken and the author does fix it. Could you please suggest a way to do it?
Thanks in advance.
What is “elephas”?
Hi Jason,
Elephas and Dist-Keras are both Keras extensions that allow distributed deep learning (I tried Elephas but I am unable to run it) with spark.
BTW: I have used so many of your examples to learn how to rite keras based models. A big thanks for being so generous for us.
Thanks.
https://github.com/maxpumperla/elephas
Thanks for sharing.
Great tutorial. I wasted a lot of time trying to find a solution in Keras documentation, but it was worthless… I wonder why they would not clear things like this wonderful tutorial does. Anyway, thanks again and keep the great job!
I’m happy it helped!
my problem is that one of my keras encoder-decoder works on gpu only for batch_size=1. for cpu there is no problem. do understand how this is related with gpu/cpu.
I don’t know sorry, maybe run it on the CPU instead?
Hi jason, great tutorial. But I want to ask that what is “LSTM friendly format” for input_layer.
Data must have a 3d shape of [samples, timesteps, features] when using an LSTM as the first hidden layer.
Hello, Dr. Bronwlee, I made my model with batch_size=8 and try to predict with batch_size=1. I think the third one, copying weights, would be the great choice and will try to copy your code. However, is there any chance of using Keras function “predict_on_batch” instead? Actually in my code using predict_on_batch does not make ValueErrors but different results popped up and I am not sure that it’s a consequence of “predict_on_batch” or not. In summary, could you please let me know if it’s possible to use Keras function “predict_on_batch” instead?
Perhaps it will work, I have not tried.
Thank you for an amazing tutorial. I am trying to implement a multivariate time series predictive model on sports dataset. I have a couple of question and I would really appreciate if you can help me.
The frequency(30sec) in each sample (with a unique ID per match) is the same but the samples sizes in the dataframe are not. I.e. sometimes matches take longer to finish.
Each sample or match (with 20+ features) has the same starting time index format 00:00:00, but most samples have a different end time. It could be 01:32:30, 01:33:30, 01:35:00, 01:36:30…
Can I specify the sequence length using the unique ID, I.e. different batch_size by?
And does the time format always has to be Y/M/D H/M/S or the above is accepted?
Perhaps this will help:
https://machinelearningmastery.com/data-preparation-variable-length-input-sequences-sequence-prediction/
What’s the difference of this compared to use batch_input_shape=(None, None, X.shape[2]) ??
That is used only when working with stateful (when you control the state resets) LSTMs, as far as I understand the API.
Thanks Jason.
It would be great if you could clarify the lags, timesteps, epochs, batchsize. More details described in
https://stats.stackexchange.com/questions/307744/lstm-for-time-series-lags-timesteps-epochs-batchsize
Lags are observations at prior time steps.
Lag observations can be used as timesteps for LSTM.
One epoch is comprised of 1 or more samples, where a sample is comprised of one or more timesteps and features.
A batch is a subset of sampels in an epoch. An epoch has one or more batches of samples.
Hello Jason,
I didn’t understand one thing,
When I am using LSTM the number of the prediction step (in the training) is not depend on the size of the training batch size,even according to your post (https://machinelearningmastery.com/use-different-batch-sizes-training-predicting-python-keras/) to training your model you use the series_to_supervised function only for one step forward , so why in this blog you say that you predict the number of samples as define in batch size in the training phase?
The batch size at train and prediction time must match when working with a stateful LSTM in Keras.
Perhaps a re-read of the post would make this clearer?
Hello,
If I have stacked lstm’s i must have ‘stateful=True’ at every layer or just the last one?
Typically all LSTMs layers are stateful or not.
Hello, I have multiple time series I want to fit one model on. Does it make sense to add a for and do the the same thing for n TS’s and batch_size = my standard TS size?
Sorry, I don’t follow your question, perhaps you can elaborate?
Hi Jason,
Thank you for sharing this. I have a question it would be great if you could guide me. I have kind of binary classification problem in predictive maintenance problem to predict the next failure time or time to fail of engine. I have a lot of dataset, even I pick only 5% of data that we have, its size is about 2GB. We have series dataset of almost 86 sensors. The time step is 1 minutes. We have about 1000 events that we can label that going to failure of its engine.
We selected the LSTM, but the problem is that requirement of users is to know ahead more than 1-2 days or 1440 or 2880 time steps(1 minute per time step), so we have to set window time of sequence and input_length = 1440 – 2880, it case failure when creating sequence to be trained to LSTM.
The suggestion is to split data set 450 series to be trained 20 series per time, and loop until completely trained data 450 series or as much as we have data in our large scale datasets.
Can I use your technique to do kind of this experiment? Or if you have any further suggestion or the better ways. Feel free to advise me.
Thank you so much.
Regards,
Wirasak Chomphu
Perhaps you can model the problem at a different scale/resolution?
Hi Jason,
Thank you for your response. I just want to know if the requirement of the production wants to know the time to fail minute, it will work in a real situation?
You must discover the answer via developing and evaluating a model on your specific dataset.
Hello,
Thanks for your great website and this article. I have 2 questions:
1. When I copy and paste the complete example, I get different result compare to what you put(seems you get 100% accuracy).
2. Why do you use stateful=True? And what will happen if we do not use it?
Yes, this is to be expected in many cases, see this:
https://machinelearningmastery.com/faq/single-faq/why-do-i-get-different-results-each-time-i-run-the-code
Stateful means that internal state of the LSTM is only reset when we manually reset it. Otherwise, state is reset at the end of each batch.
I also have another question:
Why did you use “compile” for new model, but not “fit” function for it? What effects does “compile” have for “old_weights”?
I understand that a Keras model must be compiled before being used.
Perhaps a compile is not needed in the final example – I thought it would be. Have you tested it without it?
No I didn’t. But I tried to change your example and test it with greater than 1 time-steps but I get errors like this:
ValueError: Error when checking input: expected lstm_114_input to have shape (1, 1) but got array with shape (60, 1)
My code looks like this but I get the above error on this line of the code: “new_model.set_weights(old_weights) ”
model = Sequential()
model.add(LSTM(units = 60, return_sequences = True, batch_input_shape = (60, 60, 1) , stateful=True))
model.add(Dropout(0.2))
model.add(LSTM(units = 60, return_sequences = True))
model.add(Dropout(0.2))
model.add(LSTM(units = 60, return_sequences = True))
model.add(Dropout(0.2))
model.add(LSTM(units = 60))
model.add(Dropout(0.2))
model.add(Dense(units = 1))
model.compile(optimizer = ‘adam’, loss = ‘mean_squared_error’)
for i in range(100):
model.fit(X_train, y_train, epochs=1, batch_size = 60 , verbose=1, shuffle=False)
model.reset_states()
new_model = Sequential()
new_model.add(LSTM(units = 60 , batch_input_shape=(1, 60 , 1) , stateful = True))
new_model.add(Dense(units = 1))
old_weights = model.get_weights()
new_model.set_weights(old_weights)
new_model.compile(optimizer = ‘adam’, loss = ‘mean_squared_error’)
new_model.reset_states()
Perhaps your data has the wrong shape?
You must change your dataset and the model.
My data is a matrix of shape “1140*60*1” for training and “1140*1” for labels. But when I use a matrix of “1*60*1” for prediction of next day, I get the error like this:
ValueError: Error when checking input: expected lstm_114_input to have shape (1, 1) but got array with shape (60, 1)
Perhaps you changed the shape of the model to (1,1), change it to (60,1) instead.
Remember, you are trying to change the batch size, not the input shape.
Hi, seems your solution doesn’t work for “timesteps > 1 “. Please improve it if you can.
Why not? What problem are you having exactly?
Statement: “Stateful means that the internal state of the LSTM is only reset when we manually reset it.”
So
model.fit(X, y, epochs=10, verbose=2, batch_size=5, shuffle=False ), wouldn’t do automatic reset_states() after each epoch right ?
And that is why we are resetting it in each iteration?
for i in range(n_epoch):
model.fit(X, y, epochs=1, batch_size=n_batch, verbose=1, shuffle=False)
model.reset_states()
It would reset after each batch within each epoch, if the model was “stateless”, the default.
With a stateful model, we can iterate the epochs manually and reset at the end of each.
What should be the batch size if the dataset size is 100K? I have a 120 different numbers in the dataset.
I want the model to give me an underlying sequence inside the dataset.
Example: Assume 1,2,3……8,10,14…..1,2,3…. 8,10,14,……as a sample dataset. Is there a model that could give me the hidden pattern ?
I recommend testing a number of different batch sizes to see what works best for your mode/data/lrate.
Hi,
I trained my model using a batch size of 32 to get the optimal weights and saved them in a file. Now, I have used your step 3, and created a new model with weights loaded from the file.And further i use model.predict() with batch_size = 1. I have a test file with 305 datapoints. When i open the file and make predictions for individual datapoints one by one as in your step 3, I get almost the same results as when i was doing a batch prediction. So this is good. However, say if I want to take some input from the user and I want to make a prediction for that particular datapoint (basically from a file with only 1 datapoint) I get a result with much lesser accuracy. Can you explain why is that happening, and any particular solution for that issue ?
Thanks in advance
Perhaps your model has overfit the training data?
I have some suggestions here:
https://machinelearningmastery.com/start-here/#better
Hi Jason
Can you explain your X and Y variables here – I feel they should be the other way around?
We are trying to predict the greater value from the smaller value? Correct?
Currently the problem is phrased as:
X Y
1 0.1 0.0
2 0.2 0.1
3 0.3 0.2
4 0.4 0.3
5 0.5 0.4
6 0.6 0.5
7 0.7 0.6
8 0.8 0.7
9 0.9 0.8
Would the following not be more correct?
Y X
1 0.1 0.0
2 0.2 0.1
3 0.3 0.2
4 0.4 0.3
5 0.5 0.4
6 0.6 0.5
7 0.7 0.6
8 0.8 0.7
9 0.9 0.8
Then things don’t look that great…
>Expected=0.1, Predicted=0.1
>Expected=0.2, Predicted=0.3
>Expected=0.3, Predicted=0.5
>Expected=0.4, Predicted=0.7
>Expected=0.5, Predicted=0.8
>Expected=0.6, Predicted=1.0
>Expected=0.7, Predicted=1.1
>Expected=0.8, Predicted=1.1
>Expected=0.9, Predicted=1.2
This might be a better place to start:
https://machinelearningmastery.com/how-to-develop-lstm-models-for-time-series-forecasting/
Hi Jason!
Thank you for your posts!
I’m a bit confused about the input shape and the batch size in keras models.
If I have an input of (150,10,1) and then a batch size of 5 when I fit the model as: model.fit(x_train,y_train, batch_size=5, epoch = 200) what is the 10 samples I have defined in the input tensor? Are those also called the batch size and why don’t they need to be the same size as in the fit?
Thank in advance
When we use a stateful LSTM, we must specify the batch size as part of the input shape.
Hi Jason,
I started out manually advancing the epochs to reset the LSTM states at the end of each epoch as you suggest. As I was trying to implement features like early stopping and model checkpoints to save only the best weights, I realized I couldn’t use the built in Keras callbacks because they get reset at the end of each epoch when we exit the fit method to reset the LSTM states.
I looked into how those callbacks are implemented in the Keras code, and I discovered that I could write my own custom callbacks and specify them to run at various points during training. So I wrote the following:
from keras.callbacks import Callback
class ResetStatesAfterEachEpoch(Callback):
def on_epoch_end(self, epoch, logs=None):
self.model.reset_states()
Including this custom ResetStatesAfterEachEpoch() callback in the callbacks list will achieve our goal of manually resetting the states of our stateful LSTM without needing to manually advance each epoch. This also means that we can use the Keras fit function and other callbacks normally. Just wanted to share in case it is useful to others.
Very nice, thanks for sharing!
Hey Leland. This is exactly what I was looking for, thanks for sharing!
The “Copy Weight” approach looks extremely useful in my current environment. Unfortunately, I’m not using Keras, as I have custom developed the whole NN stack using C++/CUDA. I was wondering, what exactly do get_weights()/set_weights() do to trim the unused weights? Does it multiply the original weight matrix by some vector? Or what else? Thanks
The number of weights is unchanged in this example, only the batch size is changed.
Hi Jason, Thanks for your answer; it gets me (almost) there.
Just to clarify, let’s say I had a training session with batchSize=20, and now I want to Infer a single sample, hence with batchSize=1.
If the number of weights is not changed, then I assume the number of input neurons is not changed either, and the 19 “orphans” simply are not loaded with values. Is this the case?
I think you may have confused “batch” with the number of “features”
Batch size is the number of samples (rows) fed to the model prior to updating the model weighs. You can learn more here:
https://machinelearningmastery.com/difference-between-a-batch-and-an-epoch/
And here:
https://machinelearningmastery.com/faq/single-faq/what-is-the-difference-between-samples-timesteps-and-features-for-lstm-input
Can you explain to me what the difference between Batch_size and timestep i’ve confused between them, and I’ve another question My dataset is big up to millions records and I do not have a standard to choose best batch_size and epochs.
Thank you,
Yes, see this:
https://machinelearningmastery.com/faq/single-faq/what-is-the-difference-between-samples-timesteps-and-features-for-lstm-input
And this:
https://machinelearningmastery.com/faq/single-faq/what-is-the-difference-between-a-batch-and-an-epoch
Thank you for this post, it really shows light about using different batch size for every case. Just run into this issue and I am glad to have found your post.
Thanks, I’m glad it helps!
Hi Jason, thanks for your post, you are helping me a lot!
I have two questions, maybe you can give me a hint with my application. In my case, I need to divide the training series into small sequences with different random size i.e:
[ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 …] -> [ [0.1 0.2 0.3] [0.3 0.4] [0.4 0.5 0.6 0.7][0.7 0.8 0.9] … ]
Using Online Learning is easy because I just feed one sequence at a time, the problem is my dataset are images, this makes the training really slow.
My first question is: is there a way to implement something like batch forecasting even when my sequences have variable size?
My second question is: How do I implement an early stop callback if I only have one epoch on Online training, do I need to check the loss myself I guess?
Thanks for the help.
What do you mean by online exactly? Updating after each example?
You can use zero padding to make all sequences the same length then masking to ignore the padded values in the model.
Here is an example of early stopping:
https://machinelearningmastery.com/how-to-stop-training-deep-neural-networks-at-the-right-time-using-early-stopping/
Yes, that is what I meant, updating after every sequence with batch_size = 1. Thanks, I will try to use the zero-padding with my image sequences!
I am a little confused as to what difference this will make?
Let’s say I compile my time series forecast model with a batch size of 50.
Now, if I predict the y values based on X_test, producing a forecast of y, for every time step,
the weights won’t get updated during this procedure, so wether I pass the model.predict a batch size of 50 or 1 should yield the same predictions?
Batch size changes the estimate of the error gradient which in turn influences the speed of learning.
I get that, but the model isn’t learning when predicting on a held out test set? So whether I predict in batches of 50, or batches of 1, should yield the same predictions?
Batch size only has an impact when training the model.
When making predictions, the model is unchanged and the batch size will not matter – it is only a computationally efficiency for blocks of memory in that case.
So why would one want different batch size when making predictions, in contrast to when training the network?
“On sequence prediction problems, it may be desirable to use a large batch size when training the network and a batch size of 1 when making predictions in order to predict the next step in the sequence.”
We might want to train with a large batch size, which is efficient, but make one step predictions during inference.
Hi Jason, thanks for another great post!
Something is not clear to me: I understand why it might be more efficient computationally speaking to forecast with smaller batch sizes.
However, this also restrict the size of the dataset: wouldn’t an expanding dataset, getting more and more data, yield better results? (Especially since we’re not re-fitting the model before each batch as this would be too long.)
I believe this is what you do in this post: https://machinelearningmastery.com/how-to-develop-lstm-models-for-multi-step-time-series-forecasting-of-household-power-consumption/
If I understand well, after each forecast your add the ground truth to the history for all future forecasts, and you simply keep the last prediction.
So I don’t understand the point, is it just for memory ressources, or is there another benefit?
Thanks again for this wonderful website!
This post is about after we have trained the final model – about how to make predictions on new data. Not about walk-forward validation.
Jason, I have a question about batch in Keras .fit method.
Let’s say I have a very big dataset, that if I specify batch size equal to length of dataset (doing a full batch gradient descent) like this:
model.fit(X_train, y_train, batch_size=)
it will yield a “Memory Error”
One solution I found is to use a mini batch, e.g. a 512 samples in a batch to update the weights.
However, my dataset is highly imbalanced, so that I need to pay more attention to AUC-PR.
What I understand:
1. Keras will update weights based on the batch size. For example, for batch_size=512, Keras will update my weights after calculating loss from 512 samples.
2. We can only calculate P-R (Precision-Recall) and AUC-PR after one epoch because calculating P-R or AUC-PR for every mini batch is just misleading (my model might be processed 500 class 0’s and 12 class 1’s for batch, and the next batch all of them have class 0).
How do I pass the dataset to my model as batch to do full batch gradient descent (only passing them as batches but not updating the weights for every batch)?
Thank you
Correct in both cases.
Perhaps use a machine with more RAM, e.g. a large EC2 instance?
The reason that you got error:
ValueError: Cannot feed value of shape (1, 1, 1) for Tensor ‘lstm_1_input:0’, which has shape ‘(9, 1, 1)’
seem to be that you are using stateful LSTM. It is not obvious to me why you need stateful=True here.
If stateful is not True, then you don’t need specify batch size in LSTM(). And you can use different batch size within training session and different batch size between training and prediction. Right? Thanks.
The problem only occurs when using stateful lstms (from memory) that’s the point of the tutorial.
hi,Jason.
How to apply LSTM in 3D coordinate prediction?
Perhaps change your LSTM to predict 3 numbers – with 3 nodes in the output layer.
Thanks
Hello Jason
i want to predict final cost and duration of projects (project management) with LSTM (for example 10 project in common field for train and 2 project for test), but one thing i didnt when
my thesis proposal of my thesis ,is every project is unique pattern in context of time series and how i handle this problem?
Perhaps start with this framework:
https://machinelearningmastery.com/start-here/#process
And this:
https://machinelearningmastery.com/how-to-develop-a-skilful-time-series-forecasting-model/
Thanks for reply
Every 10 project starts from 1 in time (month or…) , how i combine together and forecast in new project??
Perhaps parallel time series normalized by relative time steps?
Get creative, experiment.
Hi sir,
I have a classification problem with a target that varies from 0 to 4 (5 classes)
I have, for example, three users.
User A: with samples, classified as 0 and 1
User B: with samples, classified as 2 and 3
User C: with samples, classified as 0 and 4
I can not combine the data because the samples may correspond to the same period. This is if I combine User A with User B and order the data when eventually I trie to build the sliding window the dataset will become inconsistent because I will have data that belongs to two differents users.
Is possible to train the same LSTM with User A, and after with User B and so one? Should in that case call reset_state every time I fit the model with a different User?
If this is not the best approach, have you some insight into how it can be done?
Thanks in advance!
Not sure I follow.
Perhaps prototype a few solutions and use them to learn more about how to frame and model your problem.
Thanks for the reply!
Just one last question: If we use a stateless LSTM there is a difference between use Epoch on a for cycle (with epoch parameter as 1 on fit) and use Epoch number on the function fit itself?
Off the cuff, I don’t think so.
Thanks for all your tutorials on the subject!
I have some comfusion with the parameters [samples, timesteps, features],
for example, why in your example with the two sequences you have decided that any sequence in a feature, and not any sequence is a sample? (with one feature)
And some other question regarding dimensions, if my data consist of rows of 9
columns (which are features), each one contains info of 3 days for a given store
(so I have for example rev_day1, customers_day1, new_customers_day1, rev_day2…
new_customers_day3. Now I want to transform it to time series, such that any row is a sample (The target is a column vector represents entire income of the shop in a week, to its many to one problem)
of 3 days, I thought of reshaping to 3 features, 3 timestamps, so the new structure will be
(For shop A)
row 1: rev_day1, customers_day1, new_customers_day1
row 2: rev_day2, customers_day2, new_customers_day2
row 3: rev_day3, customers_day3, new_customers_day3
(For shop B)
row 1: rev_day1, customers_day1, new_customers_day1
row 2: rev_day2, customers_day2, new_customers_day2
row 3: rev_day3, customers_day3, new_customers_day3
Etc for all shops
Such that for each shop is a different sample.
Does this make since or I’m confusing parameters again?
Thanks!!
Good question, I believe this will help:
https://machinelearningmastery.com/faq/single-faq/what-is-the-difference-between-samples-timesteps-and-features-for-lstm-input
Hi, Jason. Thanks for sharing this post.
I am confused in one thing: In solution 2 you set the batch size to N (Batch Size = N). You said “We would have to use all predictions made at once, or only keep the first prediction and discard the rest.”
My question is: the batch size in solution 2 has to be the length of the data (n_batch = len(X))? Or it would work the same way if 1< bath size < N and I would have to keep the first prediction and discard the rest?
Thank you in advance.
Perhaps try it for your use case and see?
Hi Jason,
I am trying use LSTM on multivariate time series data with multiple time steps. However, while I was predicting the only one value at a time, I got the following error : ValueError: Input 0 of layer sequential_13 is incompatible with the layer: expected ndim=3, found ndim=2. Full shape received: [1, 8] .. How can I fix this problem ? Please help me.
Thanks
You can either change your data to match the expectations of your model, or change the model to match your data.
Perhaps start with one of the working examples here and adapt it for your dataset:
https://machinelearningmastery.com/how-to-develop-lstm-models-for-time-series-forecasting/
Thank you so much I would never have thought of solution 3 on my own.
You’re welcome.
Hi, Jason.
Thanks for sharing this post.
Please, it is this same principle that we apply when we want to train for example 10 files excels with the same model by considering these 10 files as the sequences.
Thanks
Sorry, I don’t understand your question. Perhaps you can rephrase?
You can set a dimension’s length to None in some cases to take variable-size input. For instance an LSTM layer with input_size=(None, n_features). Why can’t you set n_batches = None?
Batch size is the number of samples fed to the model before w weight update. It cannot be none or zero.
Great platform!
question:
Timesteps is used so that lagging info can be used to create better outputs.
cant we use batchsize for the same since LTSM has memory.
for example:
lets take example of daily temp recordings for 30 days.
Using Timestep:
I can have timestep=2 and samples=28 and batchsize=1. hence shape (28,2,1)
Now cant i achieve same with batchsize=2 and timestep=1.
i this case, hiddenstate wont be reset until last 2 days have been fed so its expected cell will adjust weights at the end of weight taking into account last 2 days of temp before outputing new hidden state.
in essence, because LTSM has memory so it shud use that to learn from past recordings. why do we need timesteps in that case.
Perhaps. As long as you take control over when the state is reset (e.g. stateful LSTM).
Hi Jason,
unfortunately the neat trick of transferring weights to another model to work around batch size seems to not work using a recent Keras version (v2.4.3). Whenever I execute the script I get wrong results e.g.:
>Expected=0.0, Predicted=0.0
>Expected=0.1, Predicted=0.1
>Expected=0.2, Predicted=0.3
>Expected=0.3, Predicted=0.4
>Expected=0.4, Predicted=0.5
>Expected=0.5, Predicted=0.6
>Expected=0.6, Predicted=0.8
>Expected=0.7, Predicted=0.9
>Expected=0.8, Predicted=1.0
However, if I use the batched version for inference the predictions are correct, e.g. using this code:
model.reset_states()
yhat = model.predict(X, batch_size=3)
for _yhat, _y in zip(yhat, y):
print(‘>Expected=%.1f, Predicted=%.1f’ % (_y, _yhat[0]))
Can you reproduce this bug? Do you know if this was introduced in a recent Keras version? Can you think of a workaround?
Thanks for your continuous work
Hello Jason,
Not sure if you still take a look at these, but thanks for the tutorial, it helps with an issue I’ve been trying to wrap my head around for too long.
Wouldn’t changing the batch size to 1 in this case remove the benefit of having an LSTM model in the first place since it wouldn’t be predicting the next sequence but basically classifying the new input?
Hi Lahan…Your understanding is correct! Thank you for the feedback!