You can get the most from a machine learning algorithm by tuning its parameters, called hyperparameters.
In this post you will discover how to tune machine learning algorithms with controlled experiments in Weka.
After reading this post you will know:
- The importance of improving the performance of machine learning models by algorithm tuning.
- How to design a controlled experiment to tune the hyperparameters of a machine learning algorithm.
- How to interpret the results from tuning an experiment using statistical significance.
Kick-start your project with my new book Machine Learning Mastery With Weka, including step-by-step tutorials and clear screenshots for all examples.
Let’s get started.

How to Tune Machine Learning Algorithms in Weka
Photo by Andrei Niemimäki, some rights reserved.
Improve Performance By Tuning
Machine learning algorithms can be configured to elicit different behavior.
This is useful because it allows their behavior to be adapted to the specifics of your machine learning problem.
This is also a difficulty because you must choose how to configure an algorithm without knowing before hand which configuration is best for your problem.
Because of this, you must tune the configuration parameters of each machine learning algorithm to your problem. This is often called algorithm tuning or algorithm hyperparameter optimization.
It is an empirical process of trial and error.
You can tinker with an algorithm in order to discover the combination of parameters that result in the best performance for your problem, but this can be difficult because you must record all of the results and compare them manually.
A more robust approach is to design a controlled experiment to evaluate a number of predefined algorithm configurations and provide tools to review compare the results.
The Weka Experiment Environment provides an interface that allows you to design, execute and analyze the results from these types of experiments.
Need more help with Weka for Machine Learning?
Take my free 14-day email course and discover how to use the platform step-by-step.
Click to sign-up and also get a free PDF Ebook version of the course.
Algorithm Tuning Experiment Overview
In this tutorial we are going to define an experiment to investigate the parameters of the k-nearest neighbors (kNN) machine learning algorithm.
We are going to investigate two parameters of the kNN algorithm:
- The value of k, which is the number of neighbors to query in order to make a prediction.
- The distance metric, which is the way that neighbors are determined in query in order to make predictions.
We are going to use the Pima Indians Onset of Diabetes dataset. Each instance represents medical details for one patient and the task is to predict whether the patient will have an onset of diabetes within the next five years. There are 8 numerical input variables all have varying scales.
Top results are in the order of 77% accuracy.
This tutorial is divided into 3 parts:
- Design The Experiment
- Run The Experiment
- Review Experiment Results
You can use this experimental design as the basis for tuning the parameters of different machine learning algorithms on your own datasets.
1. Design The Experiment
In this section we are going to define the experiment.
We will select the dataset that will be used to evaluate the different algorithm configurations. We will also add multiple instances of the kNN algorithm (called IBk in Weka) each with a different algorithm configuration.
1. Open the Weka GUI Chooser
2. Click the “Experimenter” button to open the Weka Experimenter interface.
Weka Experiment Environment
3. On the “Setup” tab, click the “New” button to start a new experiment.
4. In the “Dataset” pane, click the “Add new…” button and choose data/diabetes.arff.
5. In the “Algorithms” pane, click the “Add new…” button, click the “Choose” button and select the “IBk” algorithm under the “lazy” group. Click the “OK” button to add it.
This has added kNN with k=1 and distance=Euclidean.
Repeat this process and IBk with configuration parameter configurations listed below. The k parameter can be specified in the “KNN” parameter on the algorithm configuration.
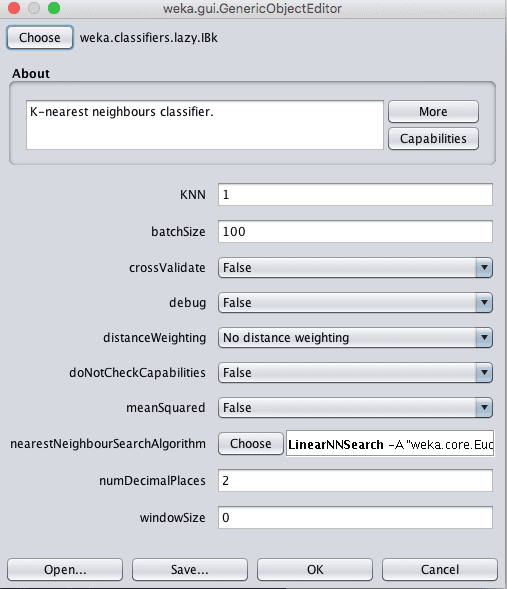
Weka k-Nearest Neighbors Algorithm Configuration
The distance measure can be changed by clicking the name of the technique for the “nearestNeighbourSearchAlgorithm” parameter to open the configuration properties for the search method, then clicking the “Choose” button for the “distanceFunction” parameter.
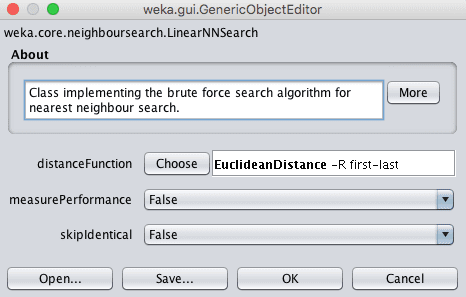
Weka Choose the Distance Function for the k-Nearest Neighbors Algorithm
Note that you can edit the configuration for an algorithm added to the experiment by clicking the “Edit selected…” button in the “Algorithms” pane.
- IBk, k=3, distanceFunction=Euclidean
- IBk, k=7, distanceFunction=Euclidean
- IBk, k=1, distanceFunction=Manhattan
- IBk, k=3, distanceFunction=Manhattan
- IBk, k=7, distanceFunction=Manhattan
Euclidean distance is a distance measure that is best used when all of the input attributes in the dataset have the same scale. Manhattan distance is a measure that is best used when the input attributes have varying scales, such as in the case of the Pima Indians onset of diabetes dataset.
We would expect that kNN with a Manhattan distance measure would achieve a better overall score from this experiment.
The experiment uses 10-fold cross validation (the default). Each configuration will be evaluated on the dataset 10 times (10 runs of 10-fold cross validation) with different random number seeds. This will result is 10 slightly different results for each evaluated algorithm configuration, a small population that we can interpret using statistical methods later.
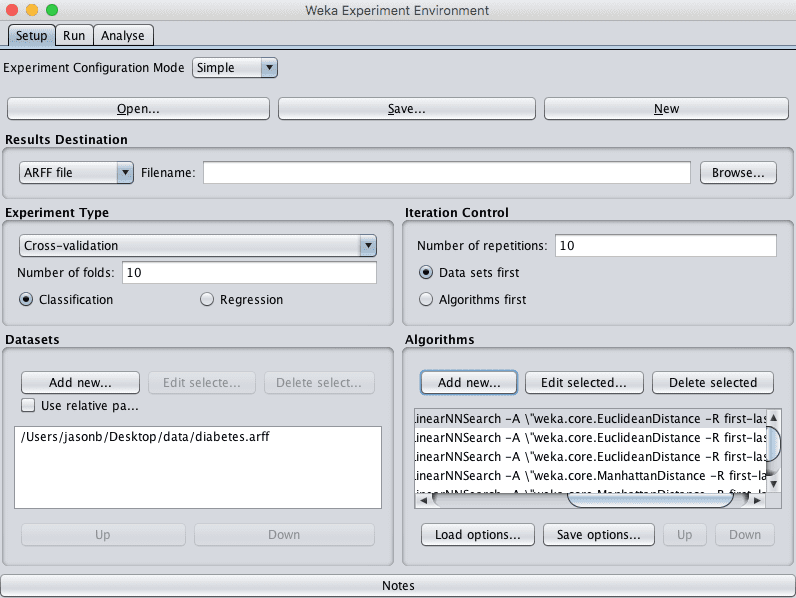
Weka Configured Algorithm Tuning Experiment
2. Run The Experiment
Now it is time to run the experiment.
1. Click the “Run” tab.
There are few options here. All you can do is start an experiment or stop a running experiment.
2. Click the “Start” button and run the experiment. It should complete in a few seconds. This is because the dataset is small.
Weka Run the Algorithm Tuning Experiment
3. Review Experiment Results
Load the results from the experiment we just executed by clicking the “Experiment” button in the “Source” pane.
Weka Load the Algorithm Tuning Experiment Results
You will see that 600 results were loaded. This is because we had 6 algorithm configurations that were each evaluated 100 times, or 10-fold cross validation multiplied by 10 repeats.
We are going to compare each algorithm configuration based on the percentage correct using pair-wise statistical significance tests. All of the default configurations.
The base for comparison is the first algorithm in the list, IBK with k=1 and distanceMeasure=Euclidean, the first algorithm added to the experiment, also the default selection.
Click the “Perform test” button in the “Actions” pane.
You will see a table of results like the one listed below:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
Tester: weka.experiment.PairedCorrectedTTester -G 4,5,6 -D 1 -R 2 -S 0.05 -result-matrix "weka.experiment.ResultMatrixPlainText -mean-prec 2 -stddev-prec 2 -col-name-width 0 -row-name-width 25 -mean-width 0 -stddev-width 0 -sig-width 0 -count-width 5 -print-col-names -print-row-names -enum-col-names" Analysing: Percent_correct Datasets: 1 Resultsets: 6 Confidence: 0.05 (two tailed) Sorted by: - Date: 8/06/16 9:55 AM Dataset (1) lazy.IBk | (2) lazy. (3) lazy. (4) lazy. (5) lazy. (6) lazy. ------------------------------------------------------------------------------------------ pima_diabetes (100) 70.62 | 73.86 v 74.45 v 69.68 71.90 73.25 ------------------------------------------------------------------------------------------ (v/ /*) | (1/0/0) (1/0/0) (0/1/0) (0/1/0) (0/1/0) Key: (1) lazy.IBk '-K 1 -W 0 -A \"weka.core.neighboursearch.LinearNNSearch -A \\\"weka.core.EuclideanDistance -R first-last\\\"\"' -3080186098777067172 (2) lazy.IBk '-K 3 -W 0 -A \"weka.core.neighboursearch.LinearNNSearch -A \\\"weka.core.EuclideanDistance -R first-last\\\"\"' -3080186098777067172 (3) lazy.IBk '-K 7 -W 0 -A \"weka.core.neighboursearch.LinearNNSearch -A \\\"weka.core.EuclideanDistance -R first-last\\\"\"' -3080186098777067172 (4) lazy.IBk '-K 1 -W 0 -A \"weka.core.neighboursearch.LinearNNSearch -A \\\"weka.core.ManhattanDistance -R first-last\\\"\"' -3080186098777067172 (5) lazy.IBk '-K 3 -W 0 -A \"weka.core.neighboursearch.LinearNNSearch -A \\\"weka.core.ManhattanDistance -R first-last\\\"\"' -3080186098777067172 (6) lazy.IBk '-K 7 -W 0 -A \"weka.core.neighboursearch.LinearNNSearch -A \\\"weka.core.ManhattanDistance -R first-last\\\"\"' -3080186098777067172 |
The results are fascinating.
We can see that in general, the Euclidean distance measure achieved better results than Manhattan but the difference between the base algorithm (k=1 with Euclidean) and all three Manhattan distance configurations was not significant (no “*” next to the result values).
We can also see that that using Euclidean distance with k=3 or k=7 does result in an accuracy that is better than the base algorithm and that this difference is statistically significant (a little “v” next to the results).
Is algorithm (3) with k=7 and distanceMeasure=Euclidean significantly better than the other results?
We can perform this comparison easily by selecting this algorithm as the basis for comparison:
- Click the “Select” button next to “Test base”.
- Click the third algorithm down with k=7 and distanceMeasure=Euclidean.
- Click the “Select” button to choose it as the base.
- Click the “Perform Test” button to create a report of the results.
Weka Choose New Test Base For Analysis of Results
You will see a table of results like the one listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
Tester: weka.experiment.PairedCorrectedTTester -G 4,5,6 -D 1 -R 2 -S 0.05 -result-matrix "weka.experiment.ResultMatrixPlainText -mean-prec 2 -stddev-prec 2 -col-name-width 0 -row-name-width 25 -mean-width 2 -stddev-width 2 -sig-width 1 -count-width 5 -print-col-names -print-row-names -enum-col-names" Analysing: Percent_correct Datasets: 1 Resultsets: 6 Confidence: 0.05 (two tailed) Sorted by: - Date: 8/06/16 10:00 AM Dataset (3) lazy.IBk | (1) lazy. (2) lazy. (4) lazy. (5) lazy. (6) lazy. ------------------------------------------------------------------------------------------ pima_diabetes (100) 74.45 | 70.62 * 73.86 69.68 * 71.90 73.25 ------------------------------------------------------------------------------------------ (v/ /*) | (0/0/1) (0/1/0) (0/0/1) (0/1/0) (0/1/0) Key: (1) lazy.IBk '-K 1 -W 0 -A \"weka.core.neighboursearch.LinearNNSearch -A \\\"weka.core.EuclideanDistance -R first-last\\\"\"' -3080186098777067172 (2) lazy.IBk '-K 3 -W 0 -A \"weka.core.neighboursearch.LinearNNSearch -A \\\"weka.core.EuclideanDistance -R first-last\\\"\"' -3080186098777067172 (3) lazy.IBk '-K 7 -W 0 -A \"weka.core.neighboursearch.LinearNNSearch -A \\\"weka.core.EuclideanDistance -R first-last\\\"\"' -3080186098777067172 (4) lazy.IBk '-K 1 -W 0 -A \"weka.core.neighboursearch.LinearNNSearch -A \\\"weka.core.ManhattanDistance -R first-last\\\"\"' -3080186098777067172 (5) lazy.IBk '-K 3 -W 0 -A \"weka.core.neighboursearch.LinearNNSearch -A \\\"weka.core.ManhattanDistance -R first-last\\\"\"' -3080186098777067172 (6) lazy.IBk '-K 7 -W 0 -A \"weka.core.neighboursearch.LinearNNSearch -A \\\"weka.core.ManhattanDistance -R first-last\\\"\"' -3080186098777067172 |
We can see that difference of k=7 and Euclidean distance is statistically significant when compared with k=1 with Euclidean or Manhattan distance, but not k=3 or 7 regardless of the distance measure.
This is helpful. It shows us that we could probably just as easily use Manhattan or Euclidean distance with k=7 or k=3 and achieve similar results.
The chosen base algorithm does have the highest accuracy at 74.45%. It is possible that this difference is statistically significant at a lower significance level, such as 20% (by setting “significance” to 0.20), but the variance would be so high (better 4 in 5 random instances) that the result might not be reliable enough.
These results are useful in another way other than seeking out the “best”. We can perhaps see a trend of increasing accuracy with increasing values of k. We could design a follow-up experiment where the distanceMeasure is fixed with Euclidean and larger k values are considered.
Summary
In this post you discovered how to design controlled experiments to tune machine learning algorithm hyperparameters.
Specifically you learned:
- About the need for algorithm parameters and the importance of tuning them empirically to your problem.
- How to design and execute a controlled experiment to tune the parameters of a machine learning algorithm in Weka.
- How to interpret the results of a controlled Experiment using statistical significance.
Do you have any questions about algorithm tuning or about this post? Ask your questions in the comments and I will do my best to answer them.







In the same way please provide tuning parameters for SVM as well as show some examples like effect resample on classifiers, please.
To my understanding, Dr. had did his best. Try to do it for yourself.
Can you please explain tuning of the parameters with respect to a regression problem (SMOreg IBK,linear regression,multilayer perceptron,REPTree(decision tree) in WEKA)
You can click the “more info” button on the algorithm configuration to learn more about each hyperparameter in Weka.
Hi Jason. Nice post 🙂 I am confused about terms here. From what I understand from another ML course… the things that we tune are called hyperparameters…. for example, in logistic regression… we can play around with alpha (learning rate). This is so that we can obtain the best parameters (i.e. the coefficients of each input variable) via, say, gradient descent. Please correct me if I am wrong here…
In this post, I think I see the terms hyperparameter and parameter to be used interchangeably. Why is this so? Thanks 🙂
Thanks.
Yes, but it is better to use systematic experimentation via the experimenter to discover the hyperparameters that work best.
Technically they are hyperparameters, but its common to simply call them parameters – which is wrong but less to say/write. More here:
https://machinelearningmastery.com/faq/single-faq/what-is-the-difference-between-a-parameter-and-a-hyperparameter