The ARIMA model for time series analysis and forecasting can be tricky to configure.
There are 3 parameters that require estimation by iterative trial and error from reviewing diagnostic plots and using 40-year-old heuristic rules.
We can automate the process of evaluating a large number of hyperparameters for the ARIMA model by using a grid search procedure.
In this tutorial, you will discover how to tune the ARIMA model using a grid search of hyperparameters in Python.
After completing this tutorial, you will know:
- A general procedure that you can use to tune the ARIMA hyperparameters for a rolling one-step forecast.
- How to apply ARIMA hyperparameter optimization on a standard univariate time series dataset.
- Ideas for extending the procedure for more elaborate and robust models.
Kick-start your project with my new book Time Series Forecasting With Python, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
- Updated Apr/2019: Updated the links to datasets.
- Updated Aug/2019: Updated data loading to use new API.
- Updated Dec/2020: Updated modeling for changes to the API.

How to Grid Search ARIMA Model Hyperparameters with Python
Photo by Alpha, some rights reserved.
Grid Searching Method
Diagnostic plots of the time series can be used along with heuristic rules to determine the hyperparameters of the ARIMA model.
These are good in most, but perhaps not all, situations.
We can automate the process of training and evaluating ARIMA models on different combinations of model hyperparameters. In machine learning this is called a grid search or model tuning.
In this tutorial, we will develop a method to grid search ARIMA hyperparameters for a one-step rolling forecast.
The approach is broken down into two parts:
- Evaluate an ARIMA model.
- Evaluate sets of ARIMA parameters.
The code in this tutorial makes use of the scikit-learn, Pandas, and the statsmodels Python libraries.
Stop learning Time Series Forecasting the slow way!
Take my free 7-day email course and discover how to get started (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
1. Evaluate ARIMA Model
We can evaluate an ARIMA model by preparing it on a training dataset and evaluating predictions on a test dataset.
This approach involves the following steps:
- Split the dataset into training and test sets.
- Walk the time steps in the test dataset.
- Train an ARIMA model.
- Make a one-step prediction.
- Store prediction; get and store actual observation.
- Calculate error score for predictions compared to expected values.
We can implement this in Python as a new standalone function called evaluate_arima_model() that takes a time series dataset as input as well as a tuple with the p, d, and q parameters for the model to be evaluated.
The dataset is split in two: 66% for the initial training dataset and the remaining 34% for the test dataset.
Each time step of the test set is iterated. Just one iteration provides a model that you could use to make predictions on new data. The iterative approach allows a new ARIMA model to be trained each time step.
A prediction is made each iteration and stored in a list. This is so that at the end of the test set, all predictions can be compared to the list of expected values and an error score calculated. In this case, a mean squared error score is calculated and returned.
The complete function is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# evaluate an ARIMA model for a given order (p,d,q) def evaluate_arima_model(X, arima_order): # prepare training dataset train_size = int(len(X) * 0.66) train, test = X[0:train_size], X[train_size:] history = [x for x in train] # make predictions predictions = list() for t in range(len(test)): model = ARIMA(history, order=arima_order) model_fit = model.fit() yhat = model_fit.forecast()[0] predictions.append(yhat) history.append(test[t]) # calculate out of sample error error = mean_squared_error(test, predictions) return error |
Now that we know how to evaluate one set of ARIMA hyperparameters, let’s see how we can call this function repeatedly for a grid of parameters to evaluate.
2. Iterate ARIMA Parameters
Evaluating a suite of parameters is relatively straightforward.
The user must specify a grid of p, d, and q ARIMA parameters to iterate. A model is created for each parameter and its performance evaluated by calling the evaluate_arima_model() function described in the previous section.
The function must keep track of the lowest error score observed and the configuration that caused it. This can be summarized at the end of the function with a print to standard out.
We can implement this function called evaluate_models() as a series of four loops.
There are two additional considerations. The first is to ensure the input data are floating point values (as opposed to integers or strings), as this can cause the ARIMA procedure to fail.
Second, the statsmodels ARIMA procedure internally uses numerical optimization procedures to find a set of coefficients for the model. These procedures can fail, which in turn can throw an exception. We must catch these exceptions and skip those configurations that cause a problem. This happens more often then you would think.
Additionally, it is recommended that warnings be ignored for this code to avoid a lot of noise from running the procedure. This can be done as follows:
|
1 2 |
import warnings warnings.filterwarnings("ignore") |
Finally, even with all of these protections, the underlying C and Fortran libraries may still report warnings to standard out, such as:
|
1 |
** On entry to DLASCL, parameter number 4 had an illegal value |
These have been removed from the results reported in this tutorial for brevity.
The complete procedure for evaluating a grid of ARIMA hyperparameters is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# evaluate combinations of p, d and q values for an ARIMA model def evaluate_models(dataset, p_values, d_values, q_values): dataset = dataset.astype('float32') best_score, best_cfg = float("inf"), None for p in p_values: for d in d_values: for q in q_values: order = (p,d,q) try: mse = evaluate_arima_model(dataset, order) if mse < best_score: best_score, best_cfg = mse, order print('ARIMA%s MSE=%.3f' % (order,mse)) except: continue print('Best ARIMA%s MSE=%.3f' % (best_cfg, best_score)) |
Now that we have a procedure to grid search ARIMA hyperparameters, let’s test the procedure on two univariate time series problems.
We will start with the Shampoo Sales dataset.
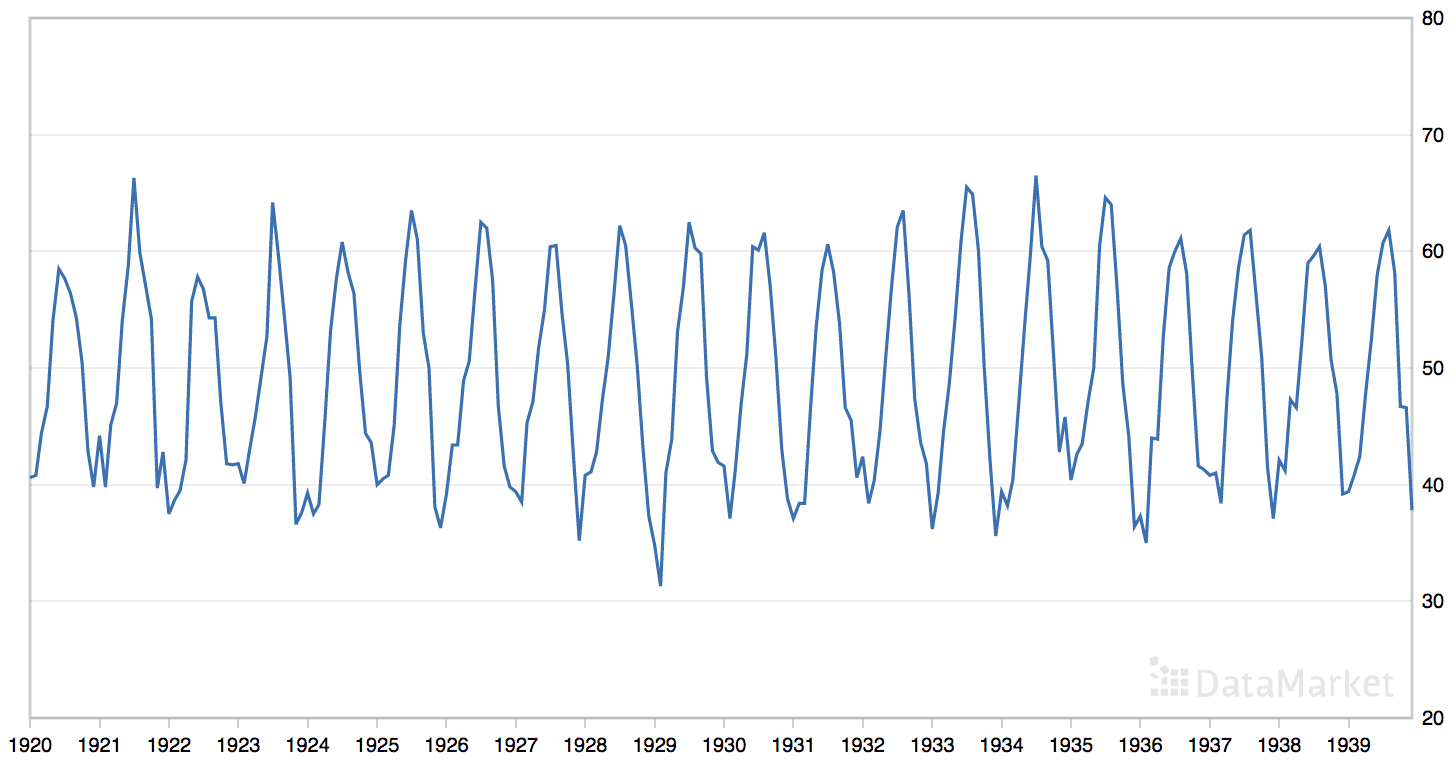
Shampoo Sales Case Study
The Shampoo Sales dataset describes the monthly number of sales of shampoo over a 3-year period.
The units are a sales count and there are 36 observations. The original dataset is credited to Makridakis, Wheelwright, and Hyndman (1998).
Download the dataset and place it into your current working directory with the filename “shampoo-sales.csv“.
The timestamps in the time series do not contain an absolute year component. We can use a custom date-parsing function when loading the data and baseline the year from 1900, as follows:
|
1 2 3 4 |
# load dataset def parser(x): return datetime.strptime('190'+x, '%Y-%m') series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser) |
Once loaded, we can specify a site of p, d, and q values to search and pass them to the evaluate_models() function.
We will try a suite of lag values (p) and just a few difference iterations (d) and residual error lag values (q).
|
1 2 3 4 5 6 |
# evaluate parameters p_values = [0, 1, 2, 4, 6, 8, 10] d_values = range(0, 3) q_values = range(0, 3) warnings.filterwarnings("ignore") evaluate_models(series.values, p_values, d_values, q_values) |
Putting this all together with the generic procedures defined in the previous section, we can grid search ARIMA hyperparameters in the Shampoo Sales dataset.
The complete code example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
# grid search ARIMA parameters for time series import warnings from math import sqrt from pandas import read_csv from pandas import datetime from statsmodels.tsa.arima.model import ARIMA from sklearn.metrics import mean_squared_error # evaluate an ARIMA model for a given order (p,d,q) def evaluate_arima_model(X, arima_order): # prepare training dataset train_size = int(len(X) * 0.66) train, test = X[0:train_size], X[train_size:] history = [x for x in train] # make predictions predictions = list() for t in range(len(test)): model = ARIMA(history, order=arima_order) model_fit = model.fit() yhat = model_fit.forecast()[0] predictions.append(yhat) history.append(test[t]) # calculate out of sample error rmse = sqrt(mean_squared_error(test, predictions)) return rmse # evaluate combinations of p, d and q values for an ARIMA model def evaluate_models(dataset, p_values, d_values, q_values): dataset = dataset.astype('float32') best_score, best_cfg = float("inf"), None for p in p_values: for d in d_values: for q in q_values: order = (p,d,q) try: rmse = evaluate_arima_model(dataset, order) if rmse < best_score: best_score, best_cfg = rmse, order print('ARIMA%s RMSE=%.3f' % (order,rmse)) except: continue print('Best ARIMA%s RMSE=%.3f' % (best_cfg, best_score)) # load dataset def parser(x): return datetime.strptime('190'+x, '%Y-%m') series = read_csv('shampoo-sales.csv', header=0, index_col=0, parse_dates=True, squeeze=True, date_parser=parser) # evaluate parameters p_values = [0, 1, 2, 4, 6, 8, 10] d_values = range(0, 3) q_values = range(0, 3) warnings.filterwarnings("ignore") evaluate_models(series.values, p_values, d_values, q_values) |
Running the example prints the ARIMA parameters and MSE for each successful evaluation completed.
The best parameters of ARIMA(4, 2, 1) are reported at the end of the run with a mean squared error of 4,694.873.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
ARIMA(0, 0, 0) MSE=52425.268 ARIMA(0, 0, 1) MSE=38145.167 ARIMA(0, 0, 2) MSE=23989.567 ARIMA(0, 1, 0) MSE=18003.173 ARIMA(0, 1, 1) MSE=9558.410 ARIMA(0, 2, 0) MSE=67339.808 ARIMA(0, 2, 1) MSE=18323.163 ARIMA(1, 0, 0) MSE=23112.958 ARIMA(1, 1, 0) MSE=7121.373 ARIMA(1, 1, 1) MSE=7003.683 ARIMA(1, 2, 0) MSE=18607.980 ARIMA(2, 1, 0) MSE=5689.932 ARIMA(2, 1, 1) MSE=7759.707 ARIMA(2, 2, 0) MSE=9860.948 ARIMA(4, 1, 0) MSE=6649.594 ARIMA(4, 1, 1) MSE=6796.279 ARIMA(4, 2, 0) MSE=7596.332 ARIMA(4, 2, 1) MSE=4694.873 ARIMA(6, 1, 0) MSE=6810.080 ARIMA(6, 2, 0) MSE=6261.107 ARIMA(8, 0, 0) MSE=7256.028 ARIMA(8, 1, 0) MSE=6579.403 Best ARIMA(4, 2, 1) MSE=4694.873 |
Daily Female Births Case Study
The Daily Female Births dataset describes the number of daily female births in California in 1959.
The units are a count and there are 365 observations. The source of the dataset is credited to Newton (1988).
Download the dataset and place it in your current working directory with the filename “daily-total-female-births.csv“.
This dataset can be easily loaded directly as a Pandas Series.
|
1 2 |
# load dataset series = read_csv('daily-total-female-births.csv', header=0, index_col=0) |
To keep things simple, we will explore the same grid of ARIMA hyperparameters as in the previous section.
|
1 2 3 4 5 6 |
# evaluate parameters p_values = [0, 1, 2, 4, 6, 8, 10] d_values = range(0, 3) q_values = range(0, 3) warnings.filterwarnings("ignore") evaluate_models(series.values, p_values, d_values, q_values) |
Putting this all together, we can grid search ARIMA parameters on the Daily Female Births dataset. The complete code listing is provided below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
# grid search ARIMA parameters for time series import warnings from math import sqrt from pandas import read_csv from statsmodels.tsa.arima.model import ARIMA from sklearn.metrics import mean_squared_error # evaluate an ARIMA model for a given order (p,d,q) def evaluate_arima_model(X, arima_order): # prepare training dataset train_size = int(len(X) * 0.66) train, test = X[0:train_size], X[train_size:] history = [x for x in train] # make predictions predictions = list() for t in range(len(test)): model = ARIMA(history, order=arima_order) model_fit = model.fit() yhat = model_fit.forecast()[0] predictions.append(yhat) history.append(test[t]) # calculate out of sample error rmse = sqrt(mean_squared_error(test, predictions)) return rmse # evaluate combinations of p, d and q values for an ARIMA model def evaluate_models(dataset, p_values, d_values, q_values): dataset = dataset.astype('float32') best_score, best_cfg = float("inf"), None for p in p_values: for d in d_values: for q in q_values: order = (p,d,q) try: rmse = evaluate_arima_model(dataset, order) if rmse < best_score: best_score, best_cfg = rmse, order print('ARIMA%s RMSE=%.3f' % (order,rmse)) except: continue print('Best ARIMA%s RMSE=%.3f' % (best_cfg, best_score)) # load dataset series = read_csv('daily-total-female-births.csv', header=0, index_col=0, parse_dates=True, squeeze=True) # evaluate parameters p_values = [0, 1, 2, 4, 6, 8, 10] d_values = range(0, 3) q_values = range(0, 3) warnings.filterwarnings("ignore") evaluate_models(series.values, p_values, d_values, q_values) |
Running the example prints the ARIMA parameters and mean squared error for each configuration successfully evaluated.
The best mean parameters are reported as ARIMA(6, 1, 0) with a mean squared error of 53.187.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
ARIMA(0, 0, 0) MSE=67.063 ARIMA(0, 0, 1) MSE=62.165 ARIMA(0, 0, 2) MSE=60.386 ARIMA(0, 1, 0) MSE=84.038 ARIMA(0, 1, 1) MSE=56.653 ARIMA(0, 1, 2) MSE=55.272 ARIMA(0, 2, 0) MSE=246.414 ARIMA(0, 2, 1) MSE=84.659 ARIMA(1, 0, 0) MSE=60.876 ARIMA(1, 1, 0) MSE=65.928 ARIMA(1, 1, 1) MSE=55.129 ARIMA(1, 1, 2) MSE=55.197 ARIMA(1, 2, 0) MSE=143.755 ARIMA(2, 0, 0) MSE=59.251 ARIMA(2, 1, 0) MSE=59.487 ARIMA(2, 1, 1) MSE=55.013 ARIMA(2, 2, 0) MSE=107.600 ARIMA(4, 0, 0) MSE=59.189 ARIMA(4, 1, 0) MSE=57.428 ARIMA(4, 1, 1) MSE=55.862 ARIMA(4, 2, 0) MSE=80.207 ARIMA(6, 0, 0) MSE=58.773 ARIMA(6, 1, 0) MSE=53.187 ARIMA(6, 1, 1) MSE=57.055 ARIMA(6, 2, 0) MSE=69.753 ARIMA(8, 0, 0) MSE=56.984 ARIMA(8, 1, 0) MSE=57.290 ARIMA(8, 2, 0) MSE=66.034 ARIMA(8, 2, 1) MSE=57.884 ARIMA(10, 0, 0) MSE=57.470 ARIMA(10, 1, 0) MSE=57.359 ARIMA(10, 2, 0) MSE=65.503 ARIMA(10, 2, 1) MSE=57.878 ARIMA(10, 2, 2) MSE=58.309 Best ARIMA(6, 1, 0) MSE=53.187 |
Extensions
The grid search method used in this tutorial is simple and can easily be extended.
This section lists some ideas to extend the approach you may wish to explore.
- Seed Grid. The classical diagnostic tools of ACF and PACF plots can still be used with the results used to seed the grid of ARIMA parameters to search.
- Alternate Measures. The search seeks to optimize the out-of-sample mean squared error. This could be changed to another out-of-sample statistic, an in-sample statistic, such as AIC or BIC, or some combination of the two. You can choose a metric that is most meaningful on your project.
- Residual Diagnostics. Statistics can automatically be calculated on the residual forecast errors to provide an additional indication of the quality of the fit. Examples include statistical tests for whether the distribution of residuals is Gaussian and whether there is an autocorrelation in the residuals.
- Update Model. The ARIMA model is created from scratch for each one-step forecast. With careful inspection of the API, it may be possible to update the internal data of the model with new observations rather than recreating it from scratch.
- Preconditions. The ARIMA model can make assumptions about the time series dataset, such as normality and stationarity. These could be checked and a warning raised for a given of a dataset prior to a given model being trained.
Summary
In this tutorial, you discovered how to grid search the hyperparameters for the ARIMA model in Python.
Specifically, you learned:
- A procedure that you can use to grid search ARIMA hyperparameters for a one-step rolling forecast.
- How to apply ARIMA hyperparameters tuning on standard univariate time series datasets.
- Ideas on how to further improve grid searching of ARIMA hyperparameters.
Now it’s your turn.
Try this procedure on your favorite time series dataset. What results did you get?
Report your results in the comments below.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.





If you are willing to consider an R solution , then I can point you to the function auto.arima in the R package ‘forecast’ : https://cran.r-project.org/web/packages/forecast/forecast.pdf
This will do all the gridsearch you need without writing a single line of code .
Now , in general , the use of gridsearch for solving the hyperparameters optimization problem in machine learning models is a poor inefficient choice . It has been proven that random search is faster and Bayesian search is even faster . See this : https://www.youtube.com/watch?v=cWQDeB9WqvU (lecture by Geoff Hinton) . For Python , there is a package called hyperopt that provides this functionality : https://github.com/hyperopt/hyperopt
An intro to hyperopt is here : https://www.youtube.com/watch?v=Mp1xnPfE4PY
Thanks for the links Gerrit.
A noted difference is the optimizaiton of an out of sample statistics, i.e. test performance.
Re grid vs random search, the ARIMA grid is small enough that it can be enumerated. When working with small grids with low compute times, random search would be much less efficient.
hello I have used the evaluate model function to chose the best configuration, but it skipped those configurations that I expect the best according to the Box-Jenkins Method. what that means? and is there any way to check that configurations?
Great question Abdallah, I am frustrated by this as well.
I believe you may be able to tinker with the ARIMA configuration further, such as configuring it use or not use a trend constant.
The issue is caused by instabilities in the linalg and optimization libraries used under the covers.
You could try an alternate implementation (R?), try implementing the method from scratch by hand or perhaps try fitting a linear regression model on a version of the dataset transformed using the same ARIMA operations.
Does that help?
You are doing here one-step rolling forecast for tuning ARIMA parameters. Will the resulting model behave best for forecasting the next observation only? Let’s assume that I would like to get the best possible prediction for the period of next 30 observations. Should the parameters tuning be changed for 30 steps rolling forecast in this case?
Yes Andres, spot on. It is critically important to optimize for the outcome you require.
Amazing stuff here, man. Love it. Keep up the good work!
Thanks for your support Stuart.
Hi Jason,
Thanks for the post. However, I encountered problems while trying to parse the date column in the Shampoo Sales example. I had downloaded the data from the following link(csv format) and am using Python 3:
https://datamarket.com/data/set/22r0/sales-of-shampoo-over-a-three-year-period#!ds=22r0&display=line
I faced 2 problems during parsing:
1) The format of Month column was “1-Jan”, indicating that we need to specify “%Y-%b” instead of “%Y-%m”
2) For values >9, that is , 10-Jan, 11-Jan and so on, the parsed date will be rendered invalid. Since it will be in the format : “19010-Jan” and similar
Please find the modified function which worked for me:
def parser(x):
#the following code chunk will take care of parsing for two conditions:
#1. for dates 10
test = int(x.split(‘-‘)[0])
#print(test)
if(test < 10):
return(datetime.strptime("190"+str(x),"%Y-%b"))
else:
return(datetime.strptime("19"+str(x),"%Y-%b"))
series = read_csv('sales-of-shampoo-over-a-three-ye.csv', header=0, parse_dates=[0], index_col=0,
squeeze=True, date_parser=parser)
Please correct me if there is a mistake in the approach. Hope this helps. Thanks again for the article. Have a good day 🙂
I have tested and confirm that the example works in Python3.
Perhaps confirm that you have the same dataset, that you have removed the footer from the file, and that you have copied the code from the post exactly?
On my computer the first example script breaks with:
** On entry to DLASCL, parameter number 4 had an illegal value
so I get no best settings.
The second script breaks with “Best ArimaNone MSE=inf”
I have already removed the footer line. Any hints available?
Hey Jason
What is the difference (or benefit) of doing the grid search this way vs. using SARIMAX? (reference: https://www.digitalocean.com/community/tutorials/a-guide-to-time-series-forecasting-with-arima-in-python-3)
I have not read that post, but skimming it suggests that are using a for loop just the same as in my tutorial.
“Each time step of the test set is iterated. Just one iteration provides a model that you could use to make predictions on new data. The iterative approach allows a new ARIMA model to be trained each time step.”
First of all, thank you for this tutorial ! I am a bit confused about using your iterative approach above. My questions are:
1. Why are you adding the test example to the training set (in history) and retraining the ARIMA model ? This way each subsequent test prediction is trained on the original training set plus an element added from the prior test example. Is this to improve the test predictions by adding more training data to the model (which now includes original training + test examples )?
2. Using the predict function, can I just train an ARIMA on the training set and use the in-built predict function on the test example set aside ? What are the pitfalls using this approach ?
Thank you again !
I am using walk-forward validation, learn more here:
https://machinelearningmastery.com/backtest-machine-learning-models-time-series-forecasting/
Yes. The walk-forward validation lets you re-fit the model each step, predict does not.
What does this error mean – Best ARIMANone RMSE=inf?
No good result found Sam. Did you run the code as-is or adapt it to your problem? Perhaps debug the example?
First let me thank you for this awsome blog. Coming to my issue, I ran this code with my own dataset. I’m getting same error.After that I tried with same dataset too.Still getting same error.Please help sir.
Thanks.
What error are you getting with the exact code in the tutorial?
Hi
Were you able to fix the problem?
Hi, I’m also occured this problem. Could you solve this problem, how?
Can the amount of input data affect to the forecast? I mean, maybe the oldest lagged data is not quite correlated with the current one. If so, wouldn’t be better to limit the length of history to 500 rows, for instance? How do I find the optimal amount of training data?
It can affect the forecast. I recommend testing the amount of forecast data used. Here’s an example:
https://machinelearningmastery.com/sensitivity-analysis-history-size-forecast-skill-arima-python/
Thanks Jason, very useful! But now I have another dilemma: should I performance the gridsearch before or after finding the optimal amount of data?
That is a good question. It is also an open question.
A purist might treat the amount of training data as yet another variable to grid search.
What if the first year data do not start from first of jan and last year for instance 2019 is continued. How one must formulate accordingly?
I don’t think it matters.
I just realized that the question I asked is from this post: https://machinelearningmastery.com/sensitivity-analysis-history-size-forecast-skill-arima-python/
I have a lot of your tutorials open all the time. Very sorry. Should I repost the question there?
No need.
Check the code line (if written by yourself, not copy/pasted). Even the smallest difference results in the **cited result**. And removing the warnings module does not help either. Had faced the same issue, only by file comparison (comparing the codes in the example here and the one written by hand) did I get to the error.
This model is taking forever to load – is there something I can do to optimize performance?
Remove some data?
I have the same query.
Try running on a faster computer?
Try running with less data?
Try running with fewer configurations?
Hi.
I’m trying to fit an ARIMA model to a financial dataset and getting really poor results. The predicted trend vary widely from the real one and relative MSE is an order of magnitude higher than required. I’m having difficulties in recognizing the source of my problem.
I have several questions. Please tell me if my questions are too extensive for this discussion:
1. How do you choose the range for the grid search? ACF and PACF graphs hinted that the order of p,q is 0,0, but the relevant models still gave poor results (I’ve used aic as my error score, and the most popular model in my runs is ARIMA(0,0,0)…)
2. Another suspect is my fit-predict procedure. I fitted a model for an X hours period and predicted the next y minutes (repeat ad-infinitum). Surprisingly, using a small x value just gave worse results, not better, although the data is highly volatile.
3. Can you prove that an ARIMA model would be a poor choice for forecasting for a certain dataset? I mean, a dataset which is already stationary (differentiated), so a Dickey-Fuller test yields good results.
Looking at ACF/PACF plots can give you an idea of values to try for q and a:
https://machinelearningmastery.com/gentle-introduction-autocorrelation-partial-autocorrelation/
Your testing procedure sounds like walk-forward validation, which is what I would recommend:
https://machinelearningmastery.com/backtest-machine-learning-models-time-series-forecasting/
Yes, if the results are bad, move on to other algorithms or more data preparation. I’d recommend both to help sniff out opportunities for your data.
Thank you for your quick answers!
– I’ve looked at ACF/PACF, and they suggested p=q=0, which is indeed my chosen model according to minimal aic criterion but is still not good enough. Maybe bic/MSE error scores could yield a different result, although I’m not optimistic.
– I haven’t read the other post yet, and I have to admit I haven’t fully realized all the nitty-gritty details of your code here, but I don’t think my algorithm fits walk-forward validation, because I fit a new model each time for a fixed sized group of data points. It’s just the fixed window that moves forward. This is mainly used for statistics sake, not for improvement of the outcome model.
– Are there other useful data preparation procedures besides smoothening?
Yes, perhaps you could start here:
https://machinelearningmastery.com/start-here/#timeseries
Ah, and the last one (for now…):
4. Could data smoothening procedures improve the performance of an ARIMA model? It seems to me that if the data is naturally volatile any smoothening is bound to mess up the prediction, but this is intuition, not a mathematical proof
It may help, try it and see – the cost is low.
Hi Jason,
From the code of “calculate out of sample error” as below, is the best fitted model selected by lowest error of testing set? what can I do if I want to use the MSE and also R-square of training set to find the best fitted model?
(# calculate out of sample error
error = mean_squared_error(test, predictions)
return error)
Thank you in advance.
Good question, I’m not sure the framework can select based on two metrics. I think you can collect multiple metrics then review the array of results to make a selection.
See here:
http://scikit-learn.org/stable/modules/grid_search.html#specifying-multiple-metrics-for-evaluation
Hi Jason,
I am running hyperparameter search. How to deal situations with like:
ValueError: The computed initial AR coefficients are not stationary
You should induce stationarity, choose a different model order, or you can
pass your own start_params.
I have multiple datasets (in like 500s) and it won’t be possible for me analyze them individually. Any suggestions?
Thank you in advance
Perhaps try making your time series stationary first:
https://machinelearningmastery.com/time-series-data-stationary-python/
Or perhaps add exception handling and ignore this error.
Sounds good. Thank you, Jason!
What is the best option to choose the ranges of pdq and then pass it on the functions to predict the best pdq results based on the MSE, how to determine the range of pdq we need to pass?
Because if we pass blindly range(0,9), the whole model will take lot of time to find out the best result..
You can use the ACF and PACF plots to help get an idea of a good range.
See this post:
https://machinelearningmastery.com/gentle-introduction-autocorrelation-partial-autocorrelation/
Thank you very much Jason for a great article again.
This article(
https://www.linkedin.com/pulse/comparison-between-classical-statistical-model-arima-deep-virmani) compared ARIMA with RNN and LSTM on time series forecasting. The results of LSTM is much better than ARIMA (RMSE: 1.02 vs. 4.74). Given that the selecting p, q, d of Arima is not easy, it seems like that using ARIMA on the forecast is wise.
Charles
Interesting, thanks for sharing.
Thank you Jason, please correct me if I am wrong.
1). The most of time series issues are nonlinear issues. we have to simplify them to linear issues to apply ARIMA since ARIMA is linear model. This is why the prediction of ARIMA is always quite poor on a time series issue.
2). RNN and LSTM are able to handle nonlinear issues. Of course, its result is better than ARIMA.
3). So, people should avoid ANY linear models for the prediction of time series issues.
I have learned a lot from your articles. Many thanks to you!
lcy1031
Mostly. Indeed ARIMA are linear models that capture linear relationships.
The more pre-processing you can do your data to make the relationship is the data simpler/better exposed, the easier modeling will be regardless of the methods used.
Thank you Jason for reply.
My concern is that any pre-processing could over simply the issue, and make the prediction not reliable. So far, there is not an approach which can measure whether or not a pre-processing is valid, and could cut the important information out.
By the way, the trend and seasonality are very good features of a curve which could help the prediction a lot. Using stationary processes to remove them out is wrong.
Thank you again!
Charles
The best measure is model skill with and without the treatment to the data.
I m getting following error when I run this line
model = ARIMA(history, order=(4,1,0))
Error
TypeError: descriptor ‘__sub__’ requires a ‘datetime.datetime’ object but received a ‘int’
Sorry to hear that. Did you copy the code and data from the tutorial exactly?
Hi Jason,
I was digging into the ‘history’ list update (based on the ‘walk forward validation’), and I see that if you print out the couples ‘predicted VS forecasted’ in the way your code is written, it is actually displaying ‘forecast of the last element added to history’ VS ‘current element test[t]’ just added to ‘history’ but not forcasted yet.
I propose this change, what do you think:
* couples ‘predicted VS expected’ I meant 🙂
In walk forward validation we want the real ob added to the history (used to fit the model), not the prediction.
Otherwise we will be using a recursive multi-step prediction model (e.g. different from our goal) and skill will be much worse.
Hi Jason, thanks for your answer but I think you misunderstood what I mean, and I actually did not change what you add to the ‘history’ list.
The change I made (validated running my code with a time series example running fine) is to display the correct pairs ‘predicted VS expected’ (can you checkl my code below in my last entry?)
Sorry for the typos, below the proposed code:
Hi Jason, thanks for your wonderful session. I have ticket count from Jan2017 till Jan2018.
I have applied AREMA model , got the predicted value of test data as below this is till Jan2018, how to forecast for Feb2018 and Mar2018 which is not in database
predicted=2440.666667, expected=2593.000000
predicted=2642.187500, expected=2289.000000
predicted=2317.411765, expected=2495.000000
predicted=2533.277778, expected=3062.000000
predicted=3128.105263, expected=2719.000000
predicted=2764.650000, expected=3159.000000
predicted=3223.428571, expected=3510.000000
predicted=3587.454545, expected=3155.000000
predicted=3213.652174, expected=2628.000000
This post will show you how to make an out of sample forecast:
https://machinelearningmastery.com/make-sample-forecasts-arima-python/
Hi Jason, thank you for the great content. You wrote: “it may be possible to update the internal data of the model with new observations rather than recreating it from scratch.” I inspected the code: statsmodels/tsa/arima_model.py carefully but have not found how to compute the residuals on the new observations (how to update the model for new observations) without revising the parameters (using the model.fit method). Do you know how to do it? It’s possible in R: https://stats.stackexchange.com/a/34191/149565
Sorry, I don’t have an example.
Jason, thank you for your response. Do you know if it is possible? If so, do you have any hints? For example, I tried to rebuild the model with the new observation added to the history (variable) and reuse as many parameters from the previous model as possible (I created a new class that inherits from ARIMA). The shape of endog (the previous observations) and exog (the error terms) did not agree (and they can be transformed internally in different ways), so I omitted the exog parameter from the previous model and retrained the new model (using fit) with a single iteration. It kind of works but probably there is a better way to do it.
It might be easier to write a custom ARIMA with the features you need. There’s not a lot to it and I do find the statsmodels implementations not entirely extensible (as I am sure you’re discovering).
Okay, thank you for your answer. I appreciate it.
Hi Jason,
for my grid search, all MLE values are returned as 0. Indicating to me that possibly MLE failed to converge. However trying a few p, d and q values by hand, some combinations converge perfectly, but returning an MSE of 0.0 nonetheless.
Do you have any idea on what might cause this?
Or the model has perfect skill. Perhaps the problem us too simple?
Hey Jason!!
An extremely helpful post.
I just wanted an estimate of runtime considering I have a 6th gen, i5 processor. It’s been 2 days and the program keeps running and is showing no results. I have read most of he comments on the post and tried to debug the code. I have confirmed that the code is running but it isn’t producing any results.
Your help will be highly appreciated!!
Thanks 🙂
Perhaps add some print() statements to help see progress?
Hi I created some raw code on this here https://github.com/decisionstats/pythonfordatascience/blob/master/Quarterly%2BTime%2BSeries%2Bof%2Bthe%2BNumber%2Bof%2BAustralian%2BResidents.ipynb
basically the search function was to minimize AIC
how would this compare to gridsearch for MSE minimization
warnings.filterwarnings(“ignore”) # specify to ignore warning messages
c4=[]
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(y,
order=param,
seasonal_order=param_seasonal,
enforce_stationarity=False,
enforce_invertibility=False)
results = mod.fit()
print(‘ARIMA{}x{}12 – AIC:{}’.format(param, param_seasonal, results.aic))
c4.append(‘ARIMA{}x{}12 – AIC:{}’.format(param, param_seasonal, results.aic))
except:
continue
Nice.
hello Jason,
it is a nice article for us to learn ARIMA. But i met one problem when running “Daily Female Births Case Study”. the error is Intel MKL ERROR: Parameter 4 was incorrect on entry to DLASCL. but when running “Shampoo Sales Case Study”. it is okay.
i got this web link below.
https://stackoverflow.com/questions/46669870/keras-with-tensorflow-backend-on-gpu-mkl-error-parameter-4-was-incorrect-on-en
my mlk with 2019.0 and 2108.0 in anaconda, the problem is always there.
i cannot to make mkl down to 11.3.3
Sorry, I’m not an expert on debugging libraries and workstations.
This is great, but I’m curious:
Here we are predicting, but what about evaluating the model in itself using the AIC, BIC, or other criteria, without doing prediction.
Sorry, I don’t have an example.
Hi Jason,
I have a production question for you.
I have micro datasets (10 rows for each dataset) and it is required to have an ARIMA model for each dataset. I have 21060 datasets and i need to create 21060 ARIMA models and i have to perform grid search for each ARIMA model.
I genericized your ARIMA grid search code and ran successfully on my computer. However, i observed that creating 1000 ARIMA models (1000 grid searches) takes approximately 1 hour on my computer. Creating 21060 ARIMA models (21060 grid searches) will approximately take 21 hours, if i run the code on my computer.
My team leader asked me that can we run your code on spark environment or can we run your code on multi thread mode in order to reduce the execution time ( 21 hours).
What do you suggest me?
You can multi-thread it, here is an example:
https://machinelearningmastery.com/how-to-grid-search-sarima-model-hyperparameters-for-time-series-forecasting-in-python/
You can run it on multiple machines to get a near-linear speedup.
Hi Jason
Thanks for the article!
I ran the same code with the same database. It ran without any error but no result is printed. It prints following:
Best ARIMANone MSE=inf
any idea?
I have some suggestions here:
https://machinelearningmastery.com/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
Hi
I tried everything with the same code and the same data, still I am getting the same result
i.e Best ARIMANone MSE=inf
That is odd, are you able to confirm that statsmodels is up to date?
Hello, I had the same problem.
I think I found the answer, we should reset the index of the test set in the function “Evaluate_arima_model” since we are applying a for loop with the range of 0 to its length.
This line of code must be added in the function “Evaluate_arima_model” : test.reset_index(drop=True,inplace = True)
The function will be then:
did you run it in terminal or in anaconda?
Save to a file and run from the command line. Here’s how:
https://machinelearningmastery.com/faq/single-faq/how-do-i-run-a-script-from-the-command-line
Hi
It ran for me. In the function, instead of ‘series.values’ I used ‘series’ and it gave me the same results as shown in the example!
How do I print Predictions vs expected table?
thanks!
Nice!
Hi Jason,
I’m getting that same ” Best ARIMANone MSE=inf” error others have seen. I’m trying to run the code but with the train/test sets I had created for a project. I removed lines 2 and 3 under the preparing the data set, and just changed the instances of X to X_train, train to X_train, and test to X_test to match my previously created datasets.
Any thoughts as to where I’m going wrong? Sorry, still new to Python as well as TS.
Thanks,
Benny
Sorry to hear that, I have some ideas here that might help:
https://machinelearningmastery.com/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
i am trying a forecasting customer transaction but no output using arima model need help
Perhaps try another model, like ETS?
Hi Jason!
I’m coding this tutorial in R and I’m not getting the same results.
For instance, for shampoo dataset for ARIMA(4,2,1) the MSE I’m getting is 5508.63.
I’m thinking that maybe it’s because I’ve split the data differently than you.
Can you tell me how many obs. does your training set have for both datasets?
If this proves to not be the case, is it possible to get different results for the same dataset with the same p,d,q arguments?
If you change the code, I would expect different results.
You can discover the number of examples used by printing the shape of the numpy array.
train, test = X[0:train_size], X[train_size:] . im getting an error for this line as TypeError: slice indices must be integers or None or have an __index__ method. Same dataset. Could someone help me with this please
Perhaps cast your variables to integers, if they are floats?
e.g. train_size = int(train_size)
Hi Jason,
thank you for all your helpful posts on this blog.
I have one question on the art of searching for hyperparameters. For machine learning methods not applied to time series I usually use nested k-fold cross-validation: Two smaller test and validation sets and a big training set.
The problem I see with your approach is, that the evaluation of model performance and the tuning of model parameters uses the same data. This way, your performance estimation can potentially be biased.
Here would be a reference for this point:
https://scikit-learn.org/stable/auto_examples/model_selection/plot_nested_cross_validation_iris.html
To overcome this, I would propose on doing something like a nested walk-forward-validation, where another timestep is held out for validation purposes.
This post seems to address this (as Day-Forward-Chaining) and will hopefully be interesting: https://towardsdatascience.com/time-series-nested-cross-validation-76adba623eb9
The downside of this approach is, that you won’t have a “final” model (as Courtney Cochrane responded in the comment section), but rather a performance estimation of all the rendered models. Additionally, this a least doubles the computational costs for evaluation.
Do you have some ideas to take into account, when a single final model is desired? My idea would still be to use your approach but hold out the one last timestep for testing the final model performance. Unfortunately, this will suffer from the arbitrary choice of the test set.
We cannot use cross validation, instead we must use walk forward validation.
This is the approach I use in almost all time series posts.
You can learn more here:
https://machinelearningmastery.com/backtest-machine-learning-models-time-series-forecasting/
A final model is fit on all available data and used to make predictions on new data:
https://machinelearningmastery.com/train-final-machine-learning-model/
Hi, thanks for the article. Your effort is much appreciated.
I can not understand on what basis you have used values of p,d,q as
p_values = [0, 1, 2, 4, 6, 8, 10]
d_values = range(0, 3)
q_values = range(0, 3) to find the best values of them? If i have hour sampled data, what values should i choose. I am using auto_arima function in python and want to know what are the would be the values of max_p, max_q, start_p, d, D should pass?
I chose then arbitrarily.
You can inform the choice with ACF/PACF plots:
https://machinelearningmastery.com/gentle-introduction-autocorrelation-partial-autocorrelation/
Hey Jason,
I am using a similar implementation of the ARIMA model that you have used and I keep coming accross a ValueError. Here is the link to the stackoverflow thread:
https://stackoverflow.com/questions/57547339/arima-model-not-invertible-producing-valueerror
Do you have any idea what the issue is?
Perhaps you can summarize your problem briefly?
That’s a nice post. I ran a gridsearch and found best values of p,d,q and P,D,Q,S for SARIMAX. However, then I used the same configurations to train model on train data plus the data that was previously used as test/hold out set (during gridsearch), the model predicts exponentially large numbers, and even negative numbers. Can you give an opinion what possibly could be the reason for this and how can I avoid this situation ? Thanks.
That’s interesting.
Perhaps try scaling the data prior to modeling?
Perhaps compare the results to a naive method to see if they are really crazy?
For scaling, I did try normalizing data using (x-mean)/std method, but the problems still exists. I even tried normalizing data using (x-mean)/std, and then applying MinMax on these values (which means double normalization), still that didn’t help.
Yes, I tried comparing the results with holt-winter’s results, hotl-winter’s gave me normal positive values, but the accuracy i achieved on SARIMAX was better (on the test set obviously), that’s why i want to stick around it.
What I couldn’t understand is, for a given set of p,d,q,P,D,Q,S, SARIMAX gives very good values for a train set. But, when i used data of say 7, 8 more months (i am dealing with monthly data btw) with same configuratoins, the model behaves very abnormally (giving negative or exponential large/small values). What would cause SARIMAX to behave like that just by adding a few more data points and using the same configuration ?
That is very odd.
My gut (spidey sense) tells me that careful debugging of the model would help, and a careful review of the data + model month by month may expose why. It could be bad inputs.
For finding order and seasonal order of SARIMAX, my approach was to run an extensive gridsearch over possible parameter values and then select the best ones who had minimum weighted mape when compared to the test data. That means, I didn’t choose the best model based on AIC/BIC, instead I chose it based on which model gave me better WMAPE on my test data. Do you think this could be a reason for my model to fail when I add test data to it ? Do I need to re-tune and find best models using AIC/BIC etc. (although I know those models will not necessarily give me best mape or wmape values). Thanks
No, it sounds like you used a good strategy!
i don’t understand why do you choice p_values = [0, 1, 2, 4, 6, 8, 10]?
They were somewhat arbitrary lags.
Thanks for the great tutorials.
I have simple question that we can also make these predictions of various time series datasets like shampoo sale or daily female birth with deep learning model LSTM which give us best predictions results as compared to ARIMA or Grid search ARIMA.
Then why not to choose direct LSTM model over these models?
Typically LSTMs are terrible at univariate time series forecasting. You can learn more here:
https://machinelearningmastery.com/findings-comparing-classical-and-machine-learning-methods-for-time-series-forecasting/
Great tutorial Jason. Is there a way I could cite this page in one of my python notebooks?
Thanks.
Yes, see this:
https://machinelearningmastery.com/faq/single-faq/how-do-i-reference-or-cite-a-book-or-blog-post
Thanks Mr. Jason. A correction though: the link that you provided has a typo. Maybe the second line that reads “you might light..” is supposed to be “You might like…”.
Thanks, fixed!
Hi Jason
Thank you for the article it was exactly what I searched for. I am new to Python coming from using Eviews for my analysis and have been looking for optimization methods.
I managed to get your functions to work and applied to one of my own time series. I am finding it is very slow to process. Can you give any insight on the best way to speed up the code? Or is it naturally quite a slow process?
Thanks
Mark
You can evaluate each model configuration in a separate thread.
Ok thanks Jason, as in a CPU thread? What is the best way to add this to the code?
I think I have a few examples around.
Here is an example of multi-threaded hyperparameter search for SARIMA:
https://machinelearningmastery.com/how-to-grid-search-sarima-model-hyperparameters-for-time-series-forecasting-in-python/
Thanks again Jason. I am currently attempting to code a system that will run OLS on every combination of variables in a dataframe.
I am currently using data.iloc[:,1:n+1] and a count variable in a loop to run a regression on n-1 variables each time. I am struggling to come up with an idea to run every potential combination, do you have any thoughts?
This will calculate all combinations:
https://docs.python.org/3/library/itertools.html#itertools.combinations
Thanks again Jason. Going to be picking up some of your books at some stage!
Thanks.
Thanks for the tutorial Jason. When it is possible to grid search so many ARIMA combinations, do you see any benefit in manually iterating through a Box-Jenkins search? Even if an aim was to learn about the time series problem more deeply, then that could also be guided by grid search, couldn’t it?
You’re welcome.
I like to try both approaches. First manual to see if I understand the problem, then grid, to see if I missed something or a non-obvious solution does better.
Thanks for the answer. The temptation to just grid search rather than understanding the problem in depth, reminds me of a concern i have about advancing business intelligence tools (eg Tableau and Power BI): When such seemingly good forecasts and visualizations are possible so easily, i worry that users / customers may not realise what they are missing in terms of understanding the problem, eg realising that a forecast is a tool to explore uncertain scenarios and perhaps the behaviour of causes underlying them, rather than a crystal ball. And if they don’t realise what they are missing, then they won’t see the value in it. Do you know what i mean?
Yes, that can happen.
Do you think there are contexts (or even whole industries) where this tends to happen at least a bit more or less than others?
I’m wondering, for example, if contexts with demand for actual understanding, like investment decisions or utilities companies, might have one force pulliing them towards wanting to understand their systems better, whereas fields where success is more subjective like marketing, or longer term like public policy, perhaps run by hierachies full of politicking, might have a stronger force pulling them towards wanting a model / consultancy / crystal ball to blame some over precise forecast on when it doesn’t happen. Have you noticed that or similar at all? Or the opposite?
I suppose i’m wondering: Can you suggest any rules of thumb to finding the customers who want to deepen their understanding of a problem situation rather than those who want an overly precise crystal ball to blame?
Oh man, deep question. My answer is: probably.
I prefer solving problems like this in the inverse. Send out a call for what I can do and wait for people that are interested to put up their hand. No selling is required as everyone is already on the same page.
Thanks Jason.
You’re welcome.
Thanks for this tutorial.
I understand it’s not valid to compare models with different values of ‘d’ using AIC. If that’s true and you wanted to use AIC, then you could only use a single value of ‘d’ in your grid search? What are your thoughts on mixing AIC and MSE together to create a more extensive grid search. Do you know how Auto_ARIMA solves this?
Would you also include checking the p-values in the grid search, or is it sufficient to just select by MSE or AIC?
I’m also interested in seeding the grid using values ACF and PACF plots. Do you have any thoughts or examples around this?
Generally, I recommend selecting one metric only and use that for model selection.
Yes, results from ACF and PACF can give ideas of values to grid search. I typically seed the search manually.
To the people with
Best ARIMANone MSE=inferror:Check your imports, especially metrics.
Hi Jason .
In the ‘plot_acf’ and ‘plot_pacf’ functions from statsmodel , how do we decide on the value of ‘lags’ parameter ?
Thanks !
You can grid search or analyse the results from the graph, see this:
https://machinelearningmastery.com/gentle-introduction-autocorrelation-partial-autocorrelation/
Thanks !
You’re welcome.
Thank you for this great article, it has really helped me on a challenging time series exercise I’m undertaking!
I’ve one situation where after grid searching the parameters of the model (a SARIMA in my case), I get errors pretty much centered around zero and a constant variance, when it comes to the autocorrelation is well under the confidence interval so until there I’m fine, however I have a unique single observation in the autocorrelation (the 50th one) which has a huge negative value…
What would you recommend me to do in this special and unique case please?
Thanks in advance for your support!
Jimmy Rico
You’re welcome.
Not sure off the cuff, perhaps experiment with transforms of your raw data?
Hi Jason, this is excellent. Thank you!
I know that my data is not stationary but the best results is with d=0. So is it okay to go forward without making the data stationary?
ARIMA(8, 0, 2) MSE=30823882221855.320
Use whatever config gives the best performance.
Hello Jason! I ran your code it worked well but when i tried to insert my own dataset that have many dates with many ids too. In this case what should I put in the read_csv(‘data.csv’,header = 0 ,index_col =?) ?
Perhaps load the dataset as a dataframe first, inspect it to confirm it was loaded correctly, then retrieve just the sequence of observations for the primary variable and use that as the series (e.g. drop the date/times and ids).
So if I drop those column when we want to predict with this kind of time series prediction is it affect the performance?
In my dataset I have many columns. so how can we specified that we want to predict which one?
You can select columns using an array index, if you are new to array indexes this will help:
https://machinelearningmastery.com/gentle-introduction-n-dimensional-arrays-python-numpy/
And this:
https://machinelearningmastery.com/index-slice-reshape-numpy-arrays-machine-learning-python/
It may, you can test this.
Hi Jason. thank you for your valuable posts!
2 questions:
1) For the shampoo study, I am running it in Jupyter and the last few lines are:
ARIMA(4, 2, 1) RMSE=68.519
ARIMA(6, 0, 0) RMSE=91.283
ARIMA(6, 1, 0) RMSE=82.523
ARIMA(6, 1, 1) RMSE=66.742
ARIMA(6, 2, 0) RMSE=79.127
ARIMA(8, 1, 0) RMSE=81.112
ARIMA(10, 1, 0) RMSE=86.852
Best ARIMA(6, 1, 1) RMSE=66.742
I noticed your output does not have (6,1,1). Any thoughts to why we are getting different results?
2) There is a deprecation warning regarding ARIMA. I have tried updating the library as the warning instructed, but the RMSE values are way off. Do you think the new libraries mean we have to specify the model in a different way in order to match the older libraries? My worry is if the new library also has different algorithms meaning we cannot match results between the old and new.
You’re welcome.
Yes, we can expect different results:
https://machinelearningmastery.com/faq/single-faq/why-do-i-get-different-results-each-time-i-run-the-code
I hope to update the example soon.
@Jason First, thank you very much Jason for these amazing tutorials. Really push me to keep on learning!
@Yazan I just run this tutorial and found the same discrepancies with RMSE values. The values seen in the tutorial are the power of 2 values of “our” small RMSE results. If you remove the “sqrt” from line 24, you’ll have the same range of results than in the sample.
Why? No idea, I am just a aficionado beginner.. Maybe anyone has a better insight on why, and if this change affects the result.
You’re welcome.
Hi, thanks mr jason for your amazing blog which is really helpful for me. Well I have been trying to make a time series analysis for my data and I am currently using your way to make the program. After a trial of the code you have posted here, I get a non logic value of forecasting where I get a sales value is a negative value although using a minimum value of MSE order combination. Will you give me advice on how to correct it, thanks
You’re welcome.
Perhaps you can correct predictions with some post processing?
Perhaps you can try an alternate data preparation prior to modeling?
Perhaps you can try an alternate model configuration?
Perhaps you can try an alternate model?
Hi Jason,
Is stationarity check a must in the method? What will happen if I didn’t check? We can make assumptions on the ARIMA as mentioned below, right?
Preconditions. The ARIMA model can make assumptions about the time series dataset, such as normality and stationarity. These could be checked and a warning raised for a given of a dataset prior to a given model being trained
Thank you.
If the series is not stationary, even you get the model, it is not useful to predict the future. ARIMA (with the “I”) allows non-stationary time series to be fitted by finding the integration (I part), which is repeatedly differencing the time series until it become stationary. Hence you can see, stationary is required. Either you check it, or the model must figure this out.
Thank you so much for the reply. This is very enlightening. Will you be able to explain more on “the model must figure this out”? Can I say because I’m doing the grid search, I’m using the cross validation in the training set as well using testing set to avoid overfit, if my results are satisfactory (like judging from RMSE), it’s most likely from the models that have selected the proper I in ARIMA to make the time series stationary. In that sense, the model has figured this out and learned by itself to get a stationary time series? Else the results won’t be good?
You’re correct!
Hi Jason, could you please make an example using the ARIMAX model ?
Hi Onari…The following resource is a great starting point for this topic:
https://www.analyticsvidhya.com/blog/2021/11/basic-understanding-of-time-series-modelling-with-auto-arimax/