k-fold Cross Validation Does Not Work For Time Series Data and
Techniques That You Can Use Instead.
The goal of time series forecasting is to make accurate predictions about the future.
The fast and powerful methods that we rely on in machine learning, such as using train-test splits and k-fold cross validation, do not work in the case of time series data. This is because they ignore the temporal components inherent in the problem.
In this tutorial, you will discover how to evaluate machine learning models on time series data with Python. In the field of time series forecasting, this is called backtesting or hindcasting.
After completing this tutorial, you will know:
- The limitations of traditional methods of model evaluation from machine learning and why evaluating models on out of sample data is required.
- How to create train-test splits and multiple train-test splits of time series data for model evaluation in Python.
- How walk-forward validation provides the most realistic evaluation of machine learning models on time series data.
Kick-start your project with my new book Time Series Forecasting With Python, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
- Updated Apr/2019: Updated the link to dataset.
- Updated Aug/2019: Fixed small typo in the number of models used in walk-forward validation (thanks Eliav).
- Updated Aug/2019: Updated data loading to use new API.

How To Backtest Machine Learning Models for Time Series Forecasting
Photo by Nasa, some rights reserved.
Model Evaluation
How do we know how good a given model is?
We could evaluate it on the data used to train it. This would be invalid. It might provide insight into how the selected model works, and even how it may be improved. But, any estimate of performance on this data would be optimistic, and any decisions based on this performance would be biased.
Why?
It is helpful to take it to an extreme:
A model that remembered the timestamps and value for each observation
would achieve perfect performance.
All real models we prepare will report a pale version of this result.
When evaluating a model for time series forecasting, we are interested in the performance of the model on data that was not used to train it. In machine learning, we call this unseen or out of sample data.
We can do this by splitting up the data that we do have available. We use some to prepare the model and we hold back some data and ask the model to make predictions for that period. The evaluation of these predictions will provide a good proxy for how the model will perform when we use it operationally.
In applied machine learning, we often split our data into a train and a test set: the training set used to prepare the model and the test set used to evaluate it. We may even use k-fold cross validation that repeats this process by systematically splitting the data into k groups, each given a chance to be a held out model.
These methods cannot be directly used with time series data.
This is because they assume that there is no relationship between the observations, that each observation is independent.
This is not true of time series data, where the time dimension of observations means that we cannot randomly split them into groups. Instead, we must split data up and respect the temporal order in which values were observed.
In time series forecasting, this evaluation of models on historical data is called backtesting. In some time series domains, such as meteorology, this is called hindcasting, as opposed to forecasting.
We will look at three different methods that you can use to backtest your machine learning models on time series problems. They are:
- Train-Test split that respect temporal order of observations.
- Multiple Train-Test splits that respect temporal order of observations.
- Walk-Forward Validation where a model may be updated each time step new data is received.
First, let’s take a look at a small, univariate time series data we will use as context to understand these three backtesting methods: the Sunspot dataset.
Stop learning Time Series Forecasting the slow way!
Take my free 7-day email course and discover how to get started (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
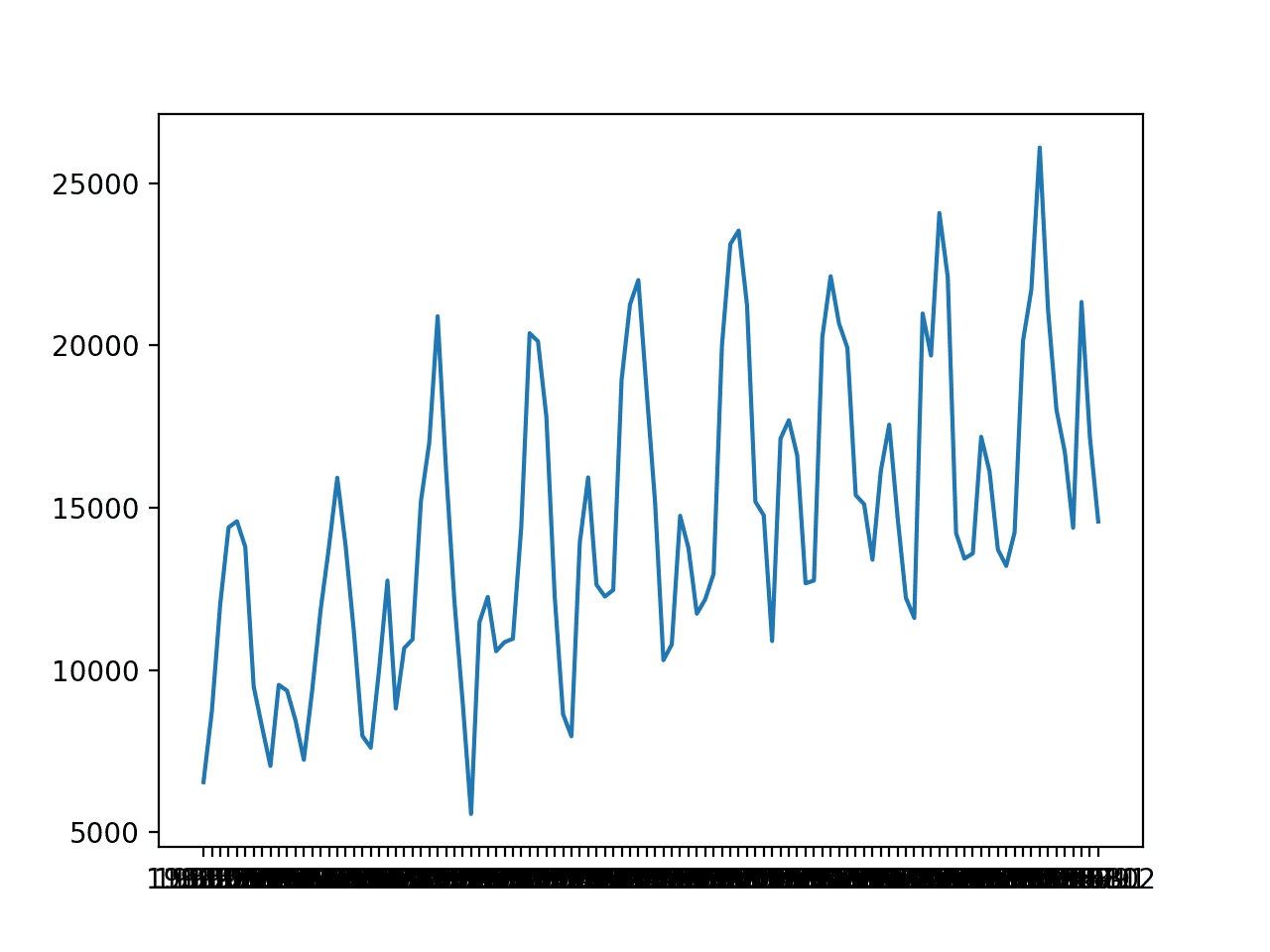
Monthly Sunspot Dataset
This dataset describes a monthly count of the number of observed sunspots for just over 230 years (1749-1983).
The units are a count and there are 2,820 observations. The source of the dataset is credited as Andrews & Herzberg (1985).
Below is a sample of the first 5 rows of data, including the header row.
|
1 2 3 4 5 6 |
"Month","Sunspots" "1749-01",58.0 "1749-02",62.6 "1749-03",70.0 "1749-04",55.7 "1749-05",85.0 |
Below is a plot of the entire dataset.
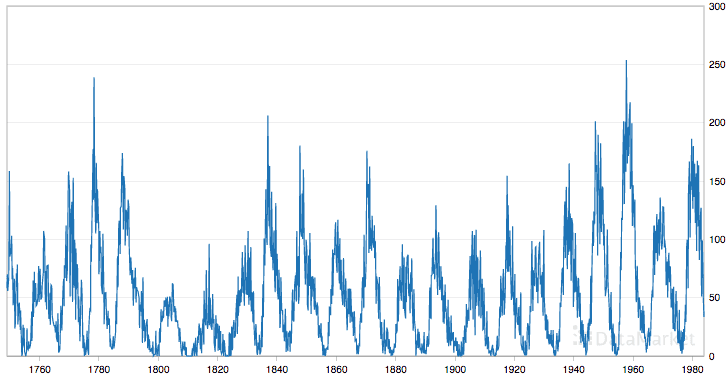
Monthly Sunspot Dataset
The dataset shows seasonality with large differences between seasons.
Download the dataset and save it into your current working directory with the filename “sunspots.csv“.
Load Sunspot Dataset
We can load the Sunspot dataset using Pandas.
|
1 2 3 4 5 6 7 |
# Load sunspot data from pandas import read_csv from matplotlib import pyplot series = read_csv('sunspots.csv', header=0, index_col=0) print(series.head()) series.plot() pyplot.show() |
Running the example prints the first 5 rows of data.
|
1 2 3 4 5 6 7 |
Month 1749-01-01 00:00:00 58.0 1749-02-01 00:00:00 62.6 1749-03-01 00:00:00 70.0 1749-04-01 00:00:00 55.7 1749-05-01 00:00:00 85.0 Name: Sunspots, dtype: float64 |
The dataset is also plotted.
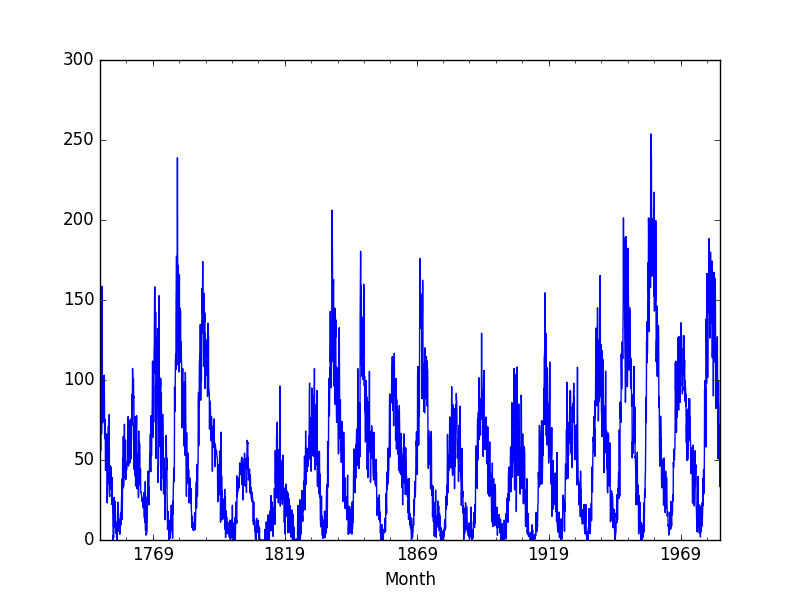
Plot of the Sunspot Dataset
Train-Test Split
You can split your dataset into training and testing subsets.
Your model can be prepared on the training dataset and predictions can be made and evaluated for the test dataset.
This can be done by selecting an arbitrary split point in the ordered list of observations and creating two new datasets. Depending on the amount of data you have available and the amount of data required, you can use splits of 50-50, 70-30 and 90-10.
It is straightforward to split data in Python.
After loading the dataset as a Pandas Series, we can extract the NumPy array of data values. The split point can be calculated as a specific index in the array. All records up to the split point are taken as the training dataset and all records from the split point to the end of the list of observations are taken as the test set.
Below is an example of this in Python using a split of 66-34.
|
1 2 3 4 5 6 7 8 |
from pandas import read_csv series = read_csv('sunspots.csv', header=0, index_col=0) X = series.values train_size = int(len(X) * 0.66) train, test = X[0:train_size], X[train_size:len(X)] print('Observations: %d' % (len(X))) print('Training Observations: %d' % (len(train))) print('Testing Observations: %d' % (len(test))) |
Running the example prints the size of the loaded dataset and the size of the train and test sets created from the split.
|
1 2 3 |
Observations: 2820 Training Observations: 1861 Testing Observations: 959 |
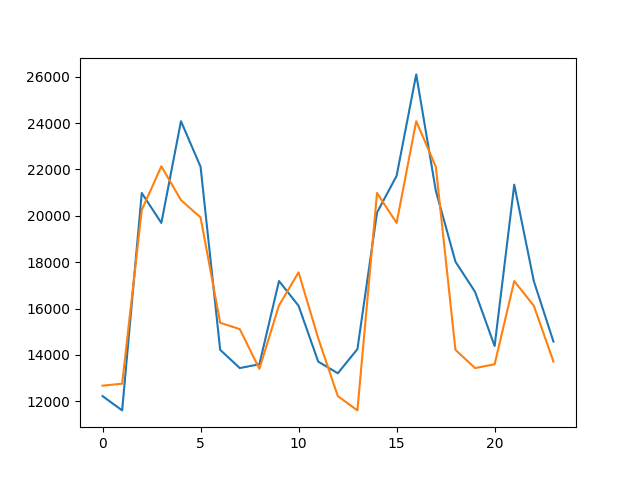
We can make this visually by plotting the training and test sets using different colors.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
from pandas import read_csv from matplotlib import pyplot series = read_csv('sunspots.csv', header=0, index_col=0) X = series.values train_size = int(len(X) * 0.66) train, test = X[0:train_size], X[train_size:len(X)] print('Observations: %d' % (len(X))) print('Training Observations: %d' % (len(train))) print('Testing Observations: %d' % (len(test))) pyplot.plot(train) pyplot.plot([None for i in train] + [x for x in test]) pyplot.show() |
Running the example plots the training dataset as blue and the test dataset as green.
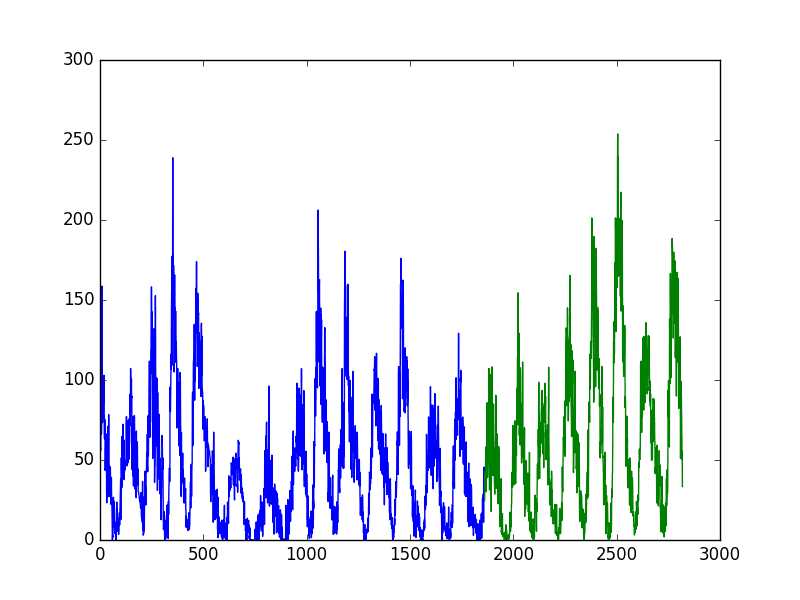
Sunspot Dataset Train-Test Split
Using a train-test split method to evaluate machine learning models is fast. Preparing the data is simple and intuitive and only one model is created and evaluated.
It is useful when you have a large amount of data so that both training and tests sets are representative of the original problem.
Next, we will look at repeating this process multiple times.
Multiple Train-Test Splits
We can repeat the process of splitting the time series into train and test sets multiple times.
This will require multiple models to be trained and evaluated, but this additional computational expense will provide a more robust estimate of the expected performance of the chosen method and configuration on unseen data.
We could do this manually by repeating the process described in the previous section with different split points.
Alternately, the scikit-learn library provides this capability for us in the TimeSeriesSplit object.
You must specify the number of splits to create and the TimeSeriesSplit to return the indexes of the train and test observations for each requested split.
The total number of training and test observations are calculated each split iteration (i) as follows:
|
1 2 |
training_size = i * n_samples / (n_splits + 1) + n_samples % (n_splits + 1) test_size = n_samples / (n_splits + 1) |
Where n_samples is the total number of observations and n_splits is the total number of splits.
Let’s make this concrete with an example. Assume we have 100 observations and we want to create 2 splits.
For the first split, the train and test sizes would be calculated as:
|
1 2 3 4 5 6 7 |
train = i * n_samples / (n_splits + 1) + n_samples % (n_splits + 1) train = 1 * 100 / (2 + 1) + 100 % (2 + 1) train = 33.3 or 33 test = n_samples / (n_splits + 1) test = 100 / (2 + 1) test = 33.3 or 33 |
Or the first 33 records are used for training and the next 33 records are used for testing.
The second split is calculated as follows:
|
1 2 3 4 5 6 7 |
train = i * n_samples / (n_splits + 1) + n_samples % (n_splits + 1) train = 2 * 100 / (2 + 1) + 100 % (2 + 1) train = 66.6 or 67 test = n_samples / (n_splits + 1) test = 100 / (2 + 1) test = 33.3 or 33 |
Or, the first 67 records are used for training and the remaining 33 records are used for testing.
You can see that the test size stays consistent. This means that performance statistics calculated on the predictions of each trained model will be consistent and can be combined and compared. It provides an apples-to-apples comparison.
What differs is the number of records used to train the model each split, offering a larger and larger history to work with. This may make an interesting aspect of the analysis of results. Alternately, this too could be controlled by holding the number of observations used to train the model consistent and only using the same number of the most recent (last) observations in the training dataset each split to train the model, 33 in this contrived example.
Let’s look at how we can apply the TimeSeriesSplit on our sunspot data.
The dataset has 2,820 observations. Let’s create 3 splits for the dataset. Using the same arithmetic above, we would expect the following train and test splits to be created:
- Split 1: 705 train, 705 test
- Split 2: 1,410 train, 705 test
- Split 3: 2,115 train, 705 test
As in the previous example, we will plot the train and test observations using separate colors. In this case, we will have 3 splits, so that will be 3 separate plots of the data.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
from pandas import read_csv from sklearn.model_selection import TimeSeriesSplit from matplotlib import pyplot series = read_csv('sunspots.csv', header=0, index_col=0) X = series.values splits = TimeSeriesSplit(n_splits=3) pyplot.figure(1) index = 1 for train_index, test_index in splits.split(X): train = X[train_index] test = X[test_index] print('Observations: %d' % (len(train) + len(test))) print('Training Observations: %d' % (len(train))) print('Testing Observations: %d' % (len(test))) pyplot.subplot(310 + index) pyplot.plot(train) pyplot.plot([None for i in train] + [x for x in test]) index += 1 pyplot.show() |
Running the example prints the number and size of the train and test sets for each split.
We can see the number of observations in each of the train and test sets for each split match the expectations calculated using the simple arithmetic above.
|
1 2 3 4 5 6 7 8 9 |
Observations: 1410 Training Observations: 705 Testing Observations: 705 Observations: 2115 Training Observations: 1410 Testing Observations: 705 Observations: 2820 Training Observations: 2115 Testing Observations: 705 |
The plot also shows the 3 splits and the growing number of total observations in each subsequent plot.
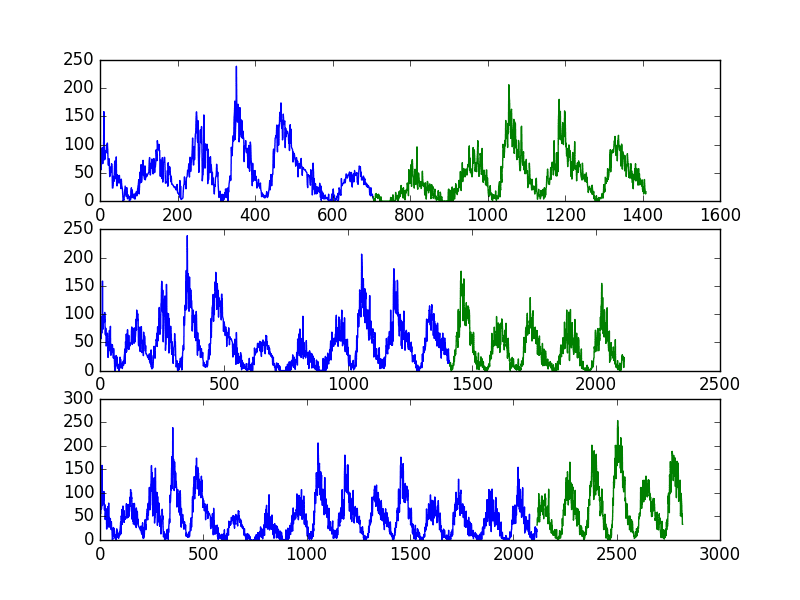
Sunspot Dataset Multiple Train-Test Split
Using multiple train-test splits will result in more models being trained, and in turn, a more accurate estimate of the performance of the models on unseen data.
A limitation of the train-test split approach is that the trained models remain fixed as they are evaluated on each evaluation in the test set.
This may not be realistic as models can be retrained as new daily or monthly observations are made available. This concern is addressed in the next section.
Walk Forward Validation
In practice, we very likely will retrain our model as new data becomes available.
This would give the model the best opportunity to make good forecasts at each time step. We can evaluate our machine learning models under this assumption.
There are few decisions to make:
1. Minimum Number of Observations. First, we must select the minimum number of observations required to train the model. This may be thought of as the window width if a sliding window is used (see next point).
2. Sliding or Expanding Window. Next, we need to decide whether the model will be trained on all data it has available or only on the most recent observations. This determines whether a sliding or expanding window will be used.
After a sensible configuration is chosen for your test-setup, models can be trained and evaluated.
- Starting at the beginning of the time series, the minimum number of samples in the window is used to train a model.
- The model makes a prediction for the next time step.
- The prediction is stored or evaluated against the known value.
- The window is expanded to include the known value and the process is repeated (go to step 1.)
Because this methodology involves moving along the time series one-time step at a time, it is often called Walk Forward Testing or Walk Forward Validation. Additionally, because a sliding or expanding window is used to train a model, this method is also referred to as Rolling Window Analysis or a Rolling Forecast.
This capability is currently not available in scikit-learn, although you could contrive the same effect with a carefully configured TimeSeriesSplit.
Below is an example of how to split data into train and test sets using the Walk Forward Validation method.
|
1 2 3 4 5 6 7 8 9 |
from pandas import read_csv from matplotlib import pyplot series = read_csv('sunspots.csv', header=0, index_col=0) X = series.values n_train = 500 n_records = len(X) for i in range(n_train, n_records): train, test = X[0:i], X[i:i+1] print('train=%d, test=%d' % (len(train), len(test))) |
Running the example simply prints the size of the training and test sets created. We can see the train set expanding teach time step and the test set fixed at one time step ahead.
Within the loop is where you would train and evaluate your model.
|
1 2 3 4 5 6 7 8 9 10 11 |
train=500, test=1 train=501, test=1 train=502, test=1 train=503, test=1 train=504, test=1 ... train=2815, test=1 train=2816, test=1 train=2817, test=1 train=2818, test=1 train=2819, test=1 |
You can see that many more models are created.
This has the benefit again of providing a much more robust estimation of how the chosen modeling method and parameters will perform in practice. This improved estimate comes at the computational cost of creating so many models.
This is not expensive if the modeling method is simple or dataset is small (as in this example), but could be an issue at scale. In the above case, 2,320 (or 2,820 – 500) models would be created and evaluated.
As such, careful attention needs to be paid to the window width and window type. These could be adjusted to contrive a test harness on your problem that is significantly less computationally expensive.
Walk-forward validation is the gold standard of model evaluation. It is the k-fold cross validation of the time series world and is recommended for your own projects.
Further Reading
- sklearn.model_selection.TimeSeriesSplit API Documentation
- Rolling-Window Analysis of Time-Series Models for more on rolling windows.
- Backtesting on Wikipedia to learn more about backtesting.
Summary
In this tutorial, you discovered how to backtest machine learning models on time series data with Python.
Specifically, you learned:
- About the importance of evaluating the performance of models on unseen or out-of-sample data.
- How to create train-test splits of time series data, and how to create multiple such splits automatically.
- How to use walk-forward validation to provide the most realistic test harness for evaluating your models.
Do you have any questions about evaluating your time series model or about this tutorial?
Ask your questions in the comments below and I will do my best to answer.






Jason,
second link from “Further Reading” should probably point to mathworks.com instead of amathworks.com, which is not found
Thanks Michael, fixed!
Many thanks, it is short and full of information.
I’m glad to hear you found it useful.
For walking forward validation it will consume a lot of time to validate after each single interation and even results won’t be much different between each iteration. Better way would be to increase h steps in each iteration and divide train and test data in that manner. Train data could be added for each h steps and test data could be for h steps for each iteration rather than single observation. This is just my sugestion from my point of view. No hard rules here.
Hi Shreyak,
Yes, that would be a sampled version of walk-forward validation, a subset.
This is pretty much what the multiple train-test splits provides in the sklearn TimeSeriesSplit object – if I understood you correctly.
Hi Dr. Jason,
Based on Shreyak’s idea of simplifying WFV, it requires you to have a common h-steps factor for total observations and minimum train samples , respectively, evenly dividing both quantities. Therefore expanding the window width by the common factor, and at same time, keeping h steps for prediction consistent at each iteration.
However, the limitation with this approach is if the common factor is 1 or even 2, or 3, and you have a large train samples, it would still default back to the traditional WFV, which is time consuming.This is where TimeSeriesSplit object comes in – that is, having a reasonable set of splits that is relevant even with large train samples.
In conclusion, it’s possible to combine multiple train-test splits method and WFV technique by expanding each train split and retraining the model, while maintaining a consistent test split.
Dr. Jason, what’s your take on this?
My take is that it is very easy to mess up and that beginner should stick to simple walk forward validation.
Sounds good, as long as whatever approach one uses worked for their problems.
Thank you!
Hello Udeh, could you add more references about your comments?
when you say ‘ Shreyak’s idea’, who are you talking about?
My query is related to walk forward validation:
Suppose a time series forecasting model is trained with a set of data and gives a good evaluation with test-set in time_range-1 and model produces a function F1. For time_range-2 and another set of training and testing data model generates function F2. Similarly for time_range-N the model generate Function FN. How the different models when combined and implemented forecast the result based on forecasting function based of local model and not the combined model of all time range model, which may possibly be producing error in forecasting.
Hi Saurabh,
Sorry, I don’t quite understand the last part of your question. Are you able to restate it?
I am just going through your posts on Time Series. Are you using any particular resource as a reference material for these things ?
A shelf of textbooks mainly 🙂
Hi Jason
Thanks so much for this in-depth post. My question is:
Which performance measure should we use in selecting the model?
For example, if I add one test subset at a time in a binary(1, 0) classification problem, the accuracy would be either 1 or 0.
In this case, how should I select a model? Should I use other measures instead?
I am building my model as stock price classification where 1 represents up, and 0 means down. I use TimeSeriesSplit and divide into T (sample size) – m (rolling window) + 1.
Thanks a lot and I look forward to listening your insights!
Hi Ian,
This is a problem specific question.
Perhaps classification accuracy on the out of sample dataset would be a good way to pick a model in your case?
Jason,
Thanks so much for answering.
If we walk one step forward every time just like what you illustrate in the Walk Forward Validation, doesn’t that mean the test dataset come from out of sample?
Hope this is not too problem specific, and thanks again in advance.
Hi Ian,
Walk forward validation is a method for estimating the skill of the model on out of sample data. We contrive out of sample and each time step one out of sample observation becomes in-sample.
We can use the same model in ops, as long as the walk-forward is performed each time a new observation is received.
Does that make sense?
Thanks Jason for an informative post!
If the time series is very long, e.g. minute values for 10 years, it will take a very long time to train. As I understand you, another way to do this is to fix the length of the training set, e.g. 2 years, but just move it, like this:
Split 1: year 1+2 train, year 3 test
Split 2: year 2+3 train, year 4 test
…
Split 8: year 8+9 train, year 10 test
Is this correct and valid?
Sounds good to me.
Also consider how valuable the older data is to fit the model. It is possible data from 10 years ago is not predictive of today, depends on the problem of course.
well how is this splits code?(8 splits)
well ? how will it do ? what is the it’s code?
Splitting a dataset is really specific to the dataset.
If you need help getting started with numpy arrays, perhaps start here:
https://machinelearningmastery.com/index-slice-reshape-numpy-arrays-machine-learning-python/
well which code should we use for this splits?
Sorry, I cannot write code for you, what problem/error are you having exactly?
Thank you for your post Jason.
I would like to ask you which model we will chose if we have implementation purpose.
In fact, for example if the time series is hour values of 3 years, walk forward could be applied in this way:
Split 1: year 1 train, year 2 test and we will get model1, error of prediction 1
Split 2: year 1+2 train, year 3 test and we will get model2, error of prediction 2
which model should we then choose ?
Great question.
Pick the model that best represents the performance/capability required for your application.
Jason,
I think that when Marwa mentioned ‘models’, she meant applying the same model (such as ARMA) on different data (corresponding to the expanding window).
I think that the walk-forward method, just like k-fold CV, gives an array of metrics whose mean somehow corresponds to the true skill of the model.
I think that when this mean is evaluated, the model should be trained on the entire dataset (check Practical Time Series Forecasting with R- Shmueli ) just like with K-fold CV.
Please correct me if I am wrong.
Regards
Walk forward validation will give a mean estimate of the skill of the model.
Walk forward validation requires some portion of the data be used to fit the model and some to evaluate it, and the portion for evaluation is stepped to be made available to training as we “walk forward”. We do not train on the entire training dataset, if we did and made a prediction, what would we compare the prediction to in order to estimate the skill of the model?
Hi Jason,
There seems to be a contradiction. The qn was “which model we will chose if we have implementation purpose.” i.e. which model to use for production. In your article: https://machinelearningmastery.com/train-final-machine-learning-model/ you state: “Once we have the estimated skill, we are finished with the resampling method. If you are using a train-test split, that means you can discard the split datasets and the trained model. They have served their purpose and are no longer needed. This is why we prefer to train the final model on all available data.”
However here you say: “Pick the model that best represents the performance/capability required for your application.”
So then what do you suggest we do for rolling out the final model to production? How to get the final model, other than to retrain the model on all data?
Hi Katya…The following resource is important when determining best “performance” of a model to be used in production:
https://machinelearningmastery.com/model-prediction-versus-interpretation-in-machine-learning/
Dear Jason,
Thanks so much for this in-depth post. My question is:
If my time series are discontinuous(such as two weeks in March and two weeks in September), How should I divide the data set?
If I use time series as supervised learning, it could lead to a sample containing data for March and September.
This question has puzzled me for a long time and I look forward to hearing from you.
I don’t have a good answer.
Perhaps try to fill in the missing time with 0s or nans.
Perhaps try to ignore the missing blocks.
Perhaps focus on building a model at a lower scale (month-wise).
Hey Jason, can you comment on Rob Hyndman’s paper stating that CV can, in fact, be used for time-series data (https://robjhyndman.com/papers/cv-wp.pdf)?
As a follow-up, would this code work in a time-series context: https://machinelearningmastery.com/use-keras-deep-learning-models-scikit-learn-python/
Thank you in advance for your guidance!
Try it and see.
I hope to when I have a pocket of time.
Is there a way to store the model fit values in such a way that we can update the model after every iteration instead of recreate an entirely new one?
My dataset has 55,000 samples and I want to run a test set of 5,000, but recreating 5,000 models would take roughly 80 hours. Thanks.
Yes, here’s how to save the model:
https://machinelearningmastery.com/save-arima-time-series-forecasting-model-python/
Thanks for responding so quickly! Say I trained a model, saved it, ran it on a test sample x1 and then iterated to test the next test sample x2. Once I load the old model, how would I add sample x1 to update the model, potentially making it perform better?
That way I am always predicting sample n+1 with a train set from 0 to n without always creating a new model for the 5000 iterations.
You would have to fit the model on just the new data or on a combination of the new and old data.
This can be done with a new model or by updating the existing model.
I do not have an example with ARIMA, but I do have examples with LSTMs here:
https://machinelearningmastery.com/update-lstm-networks-training-time-series-forecasting/
Hi, Jason
Thanks a lot for this post, I have recently gone through many for your blog post on time series forecasting and found it quite informative; especially the post on feature engineering for time series so it can be tackled with supervised learning algorithms.
Now, if I have a time series data for demand forecasting, and I have used a lot of feature engineering on the ‘date’ variable to extract all the seasonality, for example, day, month, the day of the week, if that day was a holiday, quarter, season, etc. I have also used some FE on the target variable to create lag features, min, max, range, average, etc.
My question to you is: Do I still need use backtesting/ Walk Forward Validation? or I can now use a simple k-fold cross validation since the order of time series won’t be important?
Thanks a lot. Keep doing this awesome work.
Huzefa
It really depends on your data.
In practice, I do recommend walk-forward validation when working with time series data. It is a great way to make sure you are not tricking yourself.
Jason,
Thank you for getting back. Yes, I agree with you. One more thing I realized is, I have made lags as a feature and if in any of the fold of CV a future data is used to predict past then it will act as a target leakage!
Best,
Huzefa
Absolutely!
Hi Jason
Your posts are really amazing. I have learned a lot reading your articles. I really appreciate if you can help me with a doubt regarding backtest and transforming time series to supervised learning.
May I used backtest, to identify the best lag for transforming time series to supervised learning ?
Sure.
Hi Jason,
Thank you so much for this post.
However I will have a question that might seems stupid but…
This give me a graphical version of the reality (on the train) and of my predictions (on the test). But it is not an evaluation of my model….
How do I know using those methods, if my models is great or bad?
Imagine I want to try an ARIMA (5,2) and an ARIMA (6,3). How do I do to pick the best one? How do I evaluate each one using “Walk Forward Validation”????
To evaluate the first model, I can do the mean of the error, for each split, between the prediction and the real value?
To pick the best model I can compare those mean between the 2 models?
Would it be a good evaluation methods?
Thank you again!
You can compare the predictions to the expected values and calculate an error score.
Here are some examples:
https://machinelearningmastery.com/time-series-forecasting-performance-measures-with-python/
Hi Jason,
I have a set of monthly panel data from 2000 to 2015 and I want to predict future values. In detail, I want to predict one month ahead by using a (pooled) rolling regression with a fixed window size of 5 years. (I know, there are better alternatives for panel data like regression with fixed effects, but in my case, with pooled OLS I’m getting accurate predictions.) Regression model looks like this: y_{i,t+1}= b0+ b1*x_{i,t} + b2*x2_{i,t} +… + x10_{i,t} where t is the current month and i is the id.
Furthermore, I select a new model in every step by using a dynamic model selection. In detail:
1. Take a fixed windows size of five years and split it into a training and validation set. The first 58 months as training and the month 59 as validation set.
2. Choose Explanatory Variables or rather a regression model by running a stepwise regression for model selection with the training and validation set and the Average Square Error of the validation set as a criterion.
3. Take the data from month 60 and the regression model from step 2, to make a forecast for month 61.
4. Go to step 1 and roll the window one month forward.
I couldn’t find any literature where you select a new regression model or new explanatory variables at every step of the rolling regression. Do you know if there is any literature on that?
Thank you!
Nice!
Good question. Can’t think of a good source off the top of my head, I would be sniffing around applied stats books/papers or more likely applied economics works.
Thank you!
Until now I can’t find anything on that approach and I searched several papers and books on that topic. I will keep searching! 🙂
By the way, does this approach makes sense to you?
Hang in there.
Generally, there is no one size fits all approach. Often you need to dive in and try stuff and see what suits the problem/data/project.
Correct me if I’m wrong, but it seems to me that TimeSeriesSplit is very similar to the Forward Validation technique, with the exceptions that (1) there is no option for minimum sample size (or a sliding window necessarily), and (2) the predictions are done for a larger horizon.
PS. Thanks a lot for your posts!
It is a one-time split, where as walk-forward validation splits on each time step from one point until the end of the dataset.
Does that help?
Hi Jason, I don’t see why TimeSeriesSplit makes such a “complicated” formula to create a test set of constant size. I would rather make it as a proportion of the whole window at the first iteration, and then keep that length for the remaining steps. Would it be correct ?
Yes, nice one. You have essentially described a variation on walk forward validation.
Hi Jason,
I have a query regarding Walk forward validation of TS. Let’s say I need to forecast for next 3 months (Jan-Mar 18) using last 5 years of data (Jan13-Dec 17).
In principle I would want to use Walk forward as I would like to see how well the model generalizes to unseen data. I’d use your approach which is:
1) Set Min no of observations : Jan12-Dec 16
2) Expanding TEST window : Entire 2017, which means I would forecast next 3 points (Jan-Mar 17) in iteration 1 and in next iteration, Jan 17 becomes part of train and I predict for Feb-mar-April 17.I do it for entire 2017.
My question is why do I need to RETRAIN model everytime I add 1 data point? Why can’t I just score the next 3 TEST points assuming the fact that model that I have trained before ITR1 is the best one?
Can’t I select (let’s say) top 5 models from step 1,calculate their Average for all TEST samples (3 months window) and select the one with least RMSE?.
Eagerly awaiting your reply!
You can, but the further you get from real obs as inputs the worse model skill will be come.
This post will give you some additional ideas on performing a multi-step forecast without using obs as inputs:
https://machinelearningmastery.com/multi-step-time-series-forecasting/
Hi Jason,
Thanks for the reply.
“the further you get from real obs” by that do you mean to say that I am not retraining my model using real data?
I mean that the longer the lead time – further you forecast into the future, the less stable/skillful the results.
Thanks Jason. You are indeed doing a great job.
Thanks.
Hi Jason,
Thanks a lot for your post. I am working on a demand forecasting problem for thousands of products, and I only have sales data of two years. Unit of data point can be days, but for now I aggregate into weeks. about 60% of the products have lots of zero and some bursty sales weeks. The rest have more stable sales through out the years. I tried two approaches:
– Using sales data of previous 4 weeks to train and predict sales of next week
– Using sales data of year 1 to predict the whole sales data of next year with no update to the model
My questions:
– Is there any theoretical error in these approaches? I can clarify a few things more if you need
– In this post you only talk about one time series. Can this be applied to my case where I have thousands of time series needed to be forecast at the same time?
– For this kind of problem, which algorithm tend to give best result? Can an out-of-the-box algo like XGBoost do the job? I have browsed through some papers and they introduced different methods like Neural Networks or Bayesian methods, which haven’t touched yet.
Thanks.
That sounds like a great problem.
I’m eager to dive in and offer some advice, but it would be a big time investment for me, I just don’t have the capacity. I hope to have more posts on this topic soon.
In general, I recommend testing a suite of modeling methods and framings of a problem to help you discover what works best for your specific dataset.
I’m eager to hear how you go.
Hi Jason
I am a meteorologist currently working on a time series verification problem.
My colleagues make forecasts every day and I hope to evaluate the accuracy of them.
I find that there are some time shift between our forecast and the observation. For example, we think it will be raining at 5 am tomorrow. However, the rain happens at 4 or 6. If we use normal verification method, such as contingent table, we get a miss and a false alarm. However, I think this evaluation method is inappropriate in this case since we the weather condition at 4 and 5 are not independent, we just miss the temporal attribution of these data. Can you give me some suggest about how to evaluate this kind of times series data?
Great question.
I believe there is a huge body of literature on weather forecasting verification (I used to work in this area).
Here is a great place to start:
http://www.cawcr.gov.au/projects/verification/
Hi Jason,
Is using AIC for forecasting a good method? Or should I use cross-validation while building forecasting models?
It really depends on your project goals and on your specific data.
how to estimate the AIC and BIC with NO model but only two series y and yhat?
Hi Chau…The following discussion may be of interest to you:
https://stats.stackexchange.com/questions/509044/how-to-calculate-aic-and-bic
Thank you for informative series. I would probably have to read it again, but if you could please correct me whether Sliding Window and Backtest mean the same thing. In the sense that you move the window forward step at a time?
Sliding window refers to a way of framing a time series as a supervised learning problem.
Backtesting is a general term for evaluating a model on historical data.
Dear Dr Jason,
For those having difficulty plotting the data sourced from the site https://datamarket.com/data/set/22ti/zuerich-monthly-sunspot-numbers-1749-1983 , The following may be helpful before even using Python.
Even if you imported the file from the website as a CSV file, the trouble is that there are NaN values and extraneous information at the bottom of the spreadsheet. It requires cleaning the file. Otherwise if the file is not cleaned, Python will produce error messages.
.
(1) Open the sunspot.csv file into a spreadsheet program eg MS Excel
(2) Leave the header at the top of the file alone.
(3) Scroll down to the very end of the data file (2821 rows down). Delete the rows containing Nan and text “Zuerich monthly sunspot numbers 1749-1983”.
(4) Save the file as sunspot.csv in CSV format
(3) In Python import the data as usual
Everything should be OK from that point.
Thank you,
Anthony of Sydney
I also provode all datasets in CSV format here:
https://github.com/jbrownlee/Datasets
I wonder why the monthly number of sunspots from http://www.sidc.be/silso/datafiles
vary so much from
https://github.com/jbrownlee/Datasets/blob/master/monthly-sunspots.csv
Good question, I’m not sure exactly.
My source was the CSV file on “data market”, linked in the post.
Hello Jason,
You have become a one stop website for machine learning. Thank you for all the efforts!
I am little stuck and validate my approach here, if you can:
I am trying to predict a stock market index using multiple time series: ex say many commodity indexes besides the targeted index itself. Is this approach terribly wrong? If not can you please possible point to good start point. I am really stuck here badly. Appreciate your thoughts
Thanks.
This is a common question that I answer here:
https://machinelearningmastery.com/faq/single-faq/can-you-help-me-with-machine-learning-for-finance-or-the-stock-market
Just additional comment to my previous comment is that I am trying to design a multi time series problem using supervised ml method such as Random Forest or Elastic Net
Hi Jason,
Thanks as always.
Please how do I train and evaluate my model within the loop of a Walk Forward Validation approach?
Within the Walk Forward Validation, after choosing my min training size, I created, say for, eg.
range of train to len(records):
train, test = X_obs[0:i], X_obs[i:i+1]
# Fit Model
history = model.fit(train_X, train_y, epochs=1000, batch_size=4192, validation_data= (test_X, test_y), verbose=0, shuffle=False)
# Evaluate Model
loss = model.evaluate(test_X, test_y, verbose=0)
print(loss)
model.save(‘lstm_model.h5’)
At the end, I have 10 different loss or validation scores. Is the last saved model the average of all the 10 models? How do I make predictions and calculate the RMSE for the average model?
I’m still learning the Walk Forward Validation method and will appreciate your help in guiding me on the right thing to do.
I look forward to hearing from you soon .
I recommend not using a validation set when fitting the model. The skill score is calcualted based on the predictions made within the walk-forward validation loop.
I used validation set because I wanted to monitor the validation loss value with modelcheckpoint. Thus, I would pick the best model and see how it would perform on a new or independent test set.
In addition, I would use the method or approach for the the hyperparamenter tunings to fit a final model and compare the final model with the model from modelcheckpoint.
Hi Jason, in this case, how can we monitor the validation loss during training? to develop and diagnose learning curves
It might not be the best metric to monitor. Instead, perhaps track predictive error.
so to check if my model is overfitting or not, it is enough to compare train error to the error obtained from walk forward validation?
Good question.
Generally, you will want to check that performance on the test set does not come at the expense of performance on the training set.
There are many ways to think about this, it might depend on the specifics of your problem/model and how you’ve framed the problem.
Hi Jason,
Thanks a lot for your post. You said in the Walk Forward Validation section that “”In the above case, 2,820 models would be created and evaluated.”” Is it not 2,320 since we use the 500 first observations as the minimum ?
Thanks.
Yes. Nice catch.
Hello Jason,
Thanks for the post.
Question is out of total 2320 models which Model to select for predictions?
You need some metric to measure each model and compare. That’s not shown in this post but you can see how this is done in https://machinelearningmastery.com/arima-for-time-series-forecasting-with-python/
The metrics such as AIC and BIC are examples.
Hi Jason,
Thanks for the article. I like the walk forward validation approach. I am currently using the same approach in one of the problem and have a question that I would like to discuss with you.
Q: How can we make train, validation and test split using walk forward validation approach? We generally split data into 3 parts and keep a separate test data for final evaluation. If we are keeping a window of width w and sliding it over next days, I can use to either tune hyperparameters or final validation score. What about test score and generalizability of our model?
Thanks in advance!
Good question.
Perhaps choose a period over which the model will make predictions, not be updated with true values and the holdout set can be used as validation for tuning the model?
Jason,
So, I’m wondering how these folds from Walk Forward Validation would be passed into a python pipeline or as a CV object into a sklearn model like xgboost. I’ve used GridSearchCV to create the cross-validation folds before. My project at work has sales data for a number of stores each week. I’m creating a model that will predict sales 4 weeks out by each store. Right now, I have a max of 80 weeks of data. I figured to start with a minimum train size of 52 weeks and test on the next 4 weeks. Each fold would jump 4 weeks ahead. Here, n_train = 52 and max_week = 80. My code and output are below. Thanks so much!
Code:
for i in range(n_train, max_week):
if i % 4 == 0:
train, test = df[(df.WeekCount_ID >= 1) & (df.WeekCount_ID i) & (df.WeekCount_ID <= i + 4)]
print('train=%d, test=%d' % (len(train), len(test)))
Output:
train=3155, test=260
train=3415, test=260
train=3675, test=260
train=3935, test=260
train=4195, test=272
train=4467, test=282
train=4749, test=287
Good question.
I write my own validation and grid search procedures for time series, it’s also my general recommendation in order to give more control. The sklearn tools are not suited to time series data.
Jason, thanks for the quick reply. So, for someone who is learning all of this concurrently (machine learning, time series, python, sql, etc) and not sure how to write my own python procedures, is this custom code of yours something that you cover in any of your books? If not, is this something that you would share or that I could find posted on another forum? Thanks again.
I give an example of custom code for backtesting in almost every time series example I provide.
I have a new book coming out in a week or two with many such examples.
Hi Jason,
Amazing tutorial!!!!!!!!
Let’s assume that i have training data for periods 1-100 and i want to make predictions for periods 101-120. Should i predict the target variable for period 101 and then as an input dataset predict the period 102 etc?
Many thanks
Yes, you can use the real observation is available or use the prediction as the input. The latter is called a recursive model:
https://machinelearningmastery.com/multi-step-time-series-forecasting/
Is it correct to say that this is the difference between static and dynamic forecast? Static taking the real observations for predictions and dynamic taking the predictions for further predictions?
Sounds reasonable.
Hi Jason,
May I ask two questions?
1. How to apply early stopping in walk forward validation to select the model in each walk forward step?
2. I think for time series data, we can Convert a Time Series to a Supervised Learning Problem. As the result, each sample is consist of past time step data as input and one target output. Every sample is now independent and there is no time order existed when using stateless LSTM for training. We can now shuffle all the samples and split the data as training and validation set as normal. Correct me if I am wrong.
You can do early stopping on the fitting of the model prior to making a prediction in each step of the validation process.
Perhaps. It might depend on the specifics of your domain.
Thanks for your reply.
If the model is to predict classification problem. The accuracy for each step will only be 0 or 1, which cannot be used for validation based early stopping.
Why not?
Do you mean we can make it like if for 10 epochs’ accuracy is 1 then stop training? But in this situation how to compare two models in two epochs with same accuracy=1? I mean if there are many samples for validation, I can save the best model with highest val_acc by check point function from Keras.
Not sure I follow.
Early stopping with time series is hard, but I think it is possible (happy to be proven wrong). Careful attention will need to be paid to exactly what samples are used as the validation set each step.
I don’t have a worked example, sorry.
Hi Jason,
I am new to the ML. I understood ML topics theoretically. Coming to the implementation case, really it is very hard for me. Through your website, I did some implementation work. Thanks for your help.
Coming to my question,
how to use ML binary classification concepts in case of nonstationary data (Example: EEG data)?
At present, with the help of available samples, I train the model using KV fold cross-validation.
clf=ML-Classifcationmodel();
y_pred = cross_val_predict(clf,MyX,MyY,cv=10)
every time I am getting the same results.
but if I shuffle the samples before training using below syntax, every time I am getting different results.
from sklearn.utils import shuffle
mydataset = shuffle(df1)
how to find the best model in such cases.
It’s not valid to use cross validation for time series data, regression or classification.
The train/test data must be split in such a way as to respect the temporal ordering and the model is never trained on data from the future and only tested on data from the future.
There has been a paper published here By Rob Hyndman which claims that if your problem is a purely autoregressive problem (as it would be for the framing of an ML problem as a supervised learning problem) then it is in fact valid to use K-Fold cross validation on time series, provided the residuals produced by the model are themselves uncorrelated.
The paper can be found here: https://pdfs.semanticscholar.org/b0a8/b26cb5c0836a159be7cbd574d93b265bc480.pdf
Nice find, thanks. I’ll have to give it a read.
In this post, it is explained that a Time Series problem could be reframed as a machine learning one with inputs and outputs. Could we consider in this case that each row is an independent observation and use Cross Validation , Nested Cross validation or any method for hyperparameters tuning and validation?
Nearly. The problem is that rows that contain information about the future in the training set will bias the model.
Dear Jason, thanks for your awesome work here, it helped my a lot ;)! I’m always happy to see machinelearningmastery.com in my search results list.
One question:
I want to know what window-size is the best for model.
Imagine your dataset has 2000 rows, you start with a window size of 500 to fit the model. That means i get 1500 RMSE results.
Later in that loop my windows size is for example at 1200, i use the first 1200 inputs for fitting and i only get 800 RMSE results.
Is it fair to compare the performance of both runs?
Or would it be better to ensure a static “test” length?
I have much more data available – but i want to use as less as possible to get high performance.
Regards from berlin 😉
Excellent question.
I recommend testing a suite of window sizes in order to discover the effect it has on your model for your specific dataset.
Bigger is not always better.
Sorry for my reply but i think i didn’t get the point ;).
A better example: A data set with 10000 rows, we want to know which window size performs best. For fast execution we only use the last N Values to run some tests…
TEST A) First we use the last 2000 data points to test different window sizes (200,300,400). We start our first run with win-size 200, we train on 1:200 and check performance on 201:201+horizon. We collect RMSE values for each “fold & horizon” and go further, step by step (+1) until we reach index >20004000 The smaller the window size (200), the more data i have left to test, if the window is larger, i.e. 1000 i have less data to test.
Do i have to use a “fixed” test area length to get comparable results or whats the rule of thumb here?
That’s really confusing me, many thanks…
The model evaluation across the window sizes (or whatever scheme you want to vary) should be performed on the same out of sample data.
I really love you jason 😉
A solution would be to start my test area always at i.e. index 1000 and to expand the fitting window into the past.
1….[800:999]:wns200 >> test from 1000 to 2000
1….[600:999]:wns400 >> test from 1000 to 2000
What do you think about it ?
You’re the best, many thanks again…
Sure, sounds good.
Hi Jason,
I’m very thankful for all your posts; I learn a lot with all of them.
Regarding the last option (i.e. the WFA method), I would like to be able to non-anchor the window. I have come up with the following list comprehension method:
sliceListX = [arr[i: i + window] for i in range(len(arr) – (window-1))]
Being “window” the integer value. I have managed to non anchor the window. However, I’m unable to insert another parameter for the window rolling quantity, that is, being able to move the window not only one step, but one, or two, or four. I have also posted the question on SO because I think that having a solution will benefit many others.
https://stackoverflow.com/questions/53797035/rolling-window-in-python-revisited-adding-window-rolling-quantity-as-a-paramet
Any idea on how to achieve it? (not a direct request of code).
Thanks in advance,
Sorry, I cannot give good off the cuff advice.
Finally got a working example. You can check it in the above link both the anchored version and the non anchored version. Hope it helps!
Well done!
Amazing article! Helped me a lot!
I would like to ask one question, though. If I use the shuffled splitting function from sklearn, my model is strongly biased and I have the idea that data leakage occurs.
Can you explain how this is prevented by taking a train set before 1 point in time and a test set after that point in time? I do not fully grasp the dynamics.
Many thanks!
I recommend using walk-forward validation instead.
Train-Test split that respect temporal order of observations.
and then Train shuffle only in Train dataset,eg:np.random.shuffle(Train)
Test shuffle only in Test dataset,eg:np.random.shuffle(Test)
Does it work?
Sounds reasonable.
Hello Jason, thank you for great article.
I am not sure I understand the concept of walk forward validation entirely 🙂
For example, I have a time series dataset with 3000 rows. I want to do walk forward validation. I start from the row # 500 and go ahead. Finally, I will have 2500 models created with correspondent errors.
Which one model form these 2500 should I use than for future forecasting?
Thank you!
You may or may not create a new model for each step.
You are evaluating the “model creation strategy” on average for your dataset, not a specific model.
Once you pick a strategy (e.g. model type and config), you can fit it on all available data and start making predictions. This is called creating a final model, more here:
https://machinelearningmastery.com/train-final-machine-learning-model/
Hi Jason,
I liked the explanation and the alternatives that are offered, but I’m curious about one thing. How would you implement a cross-validation approach in time-series data where the previous periods’ data are used to predict the future (for instance stock market prices)?
Walk forward validation will support whatever framing of the problem you require.
Hi, great post. I just have one doubt. Should we split our time-series data into train and test samples and then do the required normalization. Or should we normalize our series first and then do the split?
It really depends on the framing of the problem.
I have to design a test framework that tests the situation in which you expect to use the model.
Just like using all data to fit a model, you should use all reasonably available data to prepare any scaling, this applies within each walk-forward validation step.
Thank you Jason for your work.
When you work with a neural network with a sliding window, you make a new training at each step. Would it make sense to start the new step with the neural networks weights obtained in the previous one as big part of the training samples can be the same?
If so, how would you do it in Python?
Best Regards.
You can choose to refit for each window or not. I typically do not.
I have many examples, you can start here:
https://machinelearningmastery.com/start-here/#deep_learning_time_series
Hej Jason,
thank you for this well-written & well-explained tutorial. I would be very glad if you could answer one remaining question related to Multiple Train-Test Splits.
So for my understanding Multiple Train-Test Splits is a good choice to find the optimal window size for the walk forward modeling later. Do you agree on that?
Since we can check the performance based on the number of observations the model had…
Thanks! ????
Regards from Germany
Chris
Yes, it can be a good idea to test many different input window sizes to see what works well for your specific dataset.
Cool! Thanks for you reply! 🙂
Hi Jason,
Thank you for your article which is very help for me as a beginner. I’m just quiet curious that the formula of multiple train split ,splitting train_sets and test_sets, why is formed like that. it will be so grateful if you can tell me where to get more info of it.
thanks!
best regards.
What do you mean exactly?
I mean why is the formula formed like this:
training_size = i * n_samples / (n_splits + 1) + n_samples % (n_splits + 1)
test_size = n_samples / (n_splits + 1)
can i get derivation process of it somewhere ?
thank you for your reply.
Perhaps check the original code library?
get it .thank you very much.
best regards.
Hi Jason,
Thank you for this great tutorial.
What do you think about doing the multiple train-test splits in a different way:
You split the data at a certain point to a trainset and a testset.
Then you use bootstrap or a “semi” k-fold cross validation where you randomly split both the train and test sets into k folds and then train the model k times, each time on k-1 folds of the trainset and evaluate the model on k-1 folds of the testset.
What are the advantages of using the multiple train-test splits that you proposed above over this approach?
Thanks!!
Anat
Generally, you cannot use k-fold cross validation for time series data. It results in data leakage.
but I am not suggesting using an ordinary k-fold cross validation. I suggest separately splitting the train set (of past observations) into k-folds and the test set ( of later observations – after a certain point in time) into k-folds. This just allows to repeat the training / evaluation process k times for significance of the results.
I think I understand the advantage of the multiple train-test splits: it accounts for the model performance at different windows in time. The solution I proposed did not… it only evaluates the model on one period of time
Hey Jason,
Thanks for the post. I’m planning to use a supervised learning approach for time series data of 1 year (I have a retailer’s store, week level sales information). How do you suggest I go about it?
Thanks,
Adhithya
I recommend following this process:
https://machinelearningmastery.com/how-to-develop-a-skilful-time-series-forecasting-model/
These tutorials will help to get started:
https://machinelearningmastery.com/start-here/#timeseries
If my model does not use features that incorporate information about prior samples, then how does a k-fold “cheat”? It seems like if the data in any fold is likely to repeat in the future, then why is the test result from fold 1 (thus training occurs on folds 2 thru 10) in a 10 fold CV invalid? I can see how re-sampling before k-fold CV is problematic (i.e. removing the data’s temporality), but have a hard time understanding the assertion that k-fold cannot be applied to time series data – full stop. Is your assertion always true, or is it model/feature dependent? I apologise for inquiring about something that should probably be obvious. Your website is awesome and your pedagogy’s on point. Thanks for all the help.
The ordering of observations by time can cause a problem, as the model may have access to a future it may be asked to predict.
Does that help?
I can wrap my head around it at a high level and never consider using k-fold for my time-series dataset/feature/model configurations. That said, as I fall further down the ML rabbit hole, I find certain configurations that make me question the assertion. Questioning it will undoubtedly come at a cost if I don’t make an effort to rigorously prove this to myself.
Can you recommend any books that specifically address the temporal/nontemporal data issue with many examples. Please and thank you.
Not really, for the literature it is somewhat self evident (e.g. using information about the future to predict the future is bad news).
Instead, perhaps put together a small test harness with a linear model and evaluate skill under different resampling schemes. Prove to yourself that data leakage gives optimistic evaluation of model performance.
More on data leakage here:
https://machinelearningmastery.com/data-leakage-machine-learning/
I think I have a very fundamental misunderstanding of data types. While some data I have is sampled temporally, previous samples do not inform the outcome of future examples. That is, I currently consider data to be “time series” data even though no autocorrelation exist. If a set of time series data exhibits no autocorrelation, is it still considered flawed in a k-fold CV. I wish we had a whiteboard between us so you could explain this to me in 10 secs.
If the data is sequential (e.g. ordered by time), k-fold cross validation is probably a bad idea.
Hello, Jason, wonderful article !
Let me ask you something, I’m doing a binary classification in order to predict if is a good time to buy or sell a stock (-1 for sell, 1 for buy), so my target asume this two values.
I did what you said and implemented the WFV in my model, just like you did, I get the first 500 rows for training and next for testing, and so on until the end of the series.
In each iteration on the for loop, I called the .fit() function, the .predict() right after and finally I saved the model on each iteration (hoping that in the last iteration the saved model has the right weights for the task), the question is: Is this procedure right ? Should I use the last saved model to do predictions on new data ?
One last thing, in each iteration, I saved the test accuracy of the model in a list and get the mean of it, and surprisily the model get 0.9362 of mean accuracy, can we say that this model is able to predict new incoming data ?
Thanks in advance, cheers from Brasil !
Generally, I don’t believe the stock market is predictable:
https://machinelearningmastery.com/faq/single-faq/can-you-help-me-with-machine-learning-for-finance-or-the-stock-market
The evaluation procedure sounds good. I recommend fitting a final model on all available for making predictions after evaluation.
That is a nice accuracy, perhaps confirm that is reliable across many different time periods (decades).
Thank you for your reply, I’ll read this article you sent..
Saying that I’ve already trained the model and it’s “good” to go, so I start to make predictions in new data. e.g: when the market closes at 5 p.m, I’ll get the latest data and feed into the network, which will predict either -1 or 1.
1) Should I train and save the model everyday with this newest data ? (I mean, if this helps keeping performance and improving the model, worth it !)
2) Suppose that the model already did 10 predictions (in data out of train/test), and in my point of view some predictions aren’t right, should I fix the predictions and train the model it again ? What’s the smartest way to deal with this scenario ?
Thanks for providing this quality content !
Try re-training and using the old model and compare results, go with whichever strategy offers better skill for your dataset.
Perhaps use a naive method, e.g. persistance as a fallback method when you don’t trust the model in real time? Or perhaps fall back to the model from the prior day/week/month?
In fact, I won’t use it real time.. I’ll wait the market close, download the today’s prices, predict with the model and decide (based on the prediction) if I’m going to long or short..
“Perhaps use a naive method, e.g. persistance as a fallback method when you don’t trust the model in real time? Or perhaps fall back to the model from the prior day/week/month? ” I didn’t understand this part, is this the answer for the second question?
In a nutshell, the model is predicting what should I do next day. Later on I’ll try to put some prints of the predictions here. Ty again
After running the WFV, here’s a graph of the predictions: https://imgur.com/a/SUyOTzJ
As you can see, the model made some wrong predictions, could you help me improving this ? What do you suggest ? I’m thinking about editing my targets and training the model again, hoping that the noisy predictions disapear..
If you are using a neural net, I have suggestions for improving performance here:
https://machinelearningmastery.com/start-here/#better
I strongly recommend this process:
https://machinelearningmastery.com/how-to-develop-a-skilful-time-series-forecasting-model/
I see, if you’re not predicting real time, you can ignore my comment about falling back to another model.
Yes, I’m using that MLPClassifier() from sklearn.. I’l learn about RNN as soon as possible too.. Thank you for the links !
Hello Jason,
It amazes me after reading dozens of your blogs about time series.It still remains some confusions.
In my case, I try to use LSTM for univariate forecast.
1. I have read your post “How to Convert a Time Series to a Supervised Learning Problem in Python” before, and transform dataset to several sequences for supervised learning. If I want to apply backtest on my model, should I do it on raw data or transformed sequence?
2. In “Multiple Train-Test Splits” section, should the model work best in the last case(with as much data as possible)?
3. It seems ambiguous when combining “time series to supervised data” with “walk forward validation”. According to my understanding, I should train my LSTM model with supervised-learning data first, then evaluate the model with every single piece of training data.
Best regard,
Lee
The shortest path to understanding is here:
https://machinelearningmastery.com/start-here/#deep_learning_time_series
Or my book.
Or a complete tutorial, like this one:
https://machinelearningmastery.com/how-to-develop-deep-learning-models-for-univariate-time-series-forecasting/
Nevertheless:
1. Backtesting is performed on the transformed data, e.g. transform the data to a supervised learning problem after scaling/differencing/etc.
2. The idea is to estimate the performance of the model when making predictions on new data and determine if it has skill by comparing performance to a baseline model. Your chosen algorithm may or may not perform better with more history.
3. You can choose to update the model after every step forward or not. I often do not as its to computationally expensive..
Finally, LSTMs are terrible at univariate time series forecasting:
https://machinelearningmastery.com/findings-comparing-classical-and-machine-learning-methods-for-time-series-forecasting/
Use an SARIMA or ETS instead.
Hello Jason,
Thank you for your reply so soon.
I got a really long time series in my case, namely a giant dataset. It does perform well in my two-layer-LSTM with such an amount of data(hope it performs well operationally).
I would try other methods later.
Best regard,
Lee
Great!
Typo:
In question 2: “with as much data as possible” -> “with as much training data as possible”
Hey, i think you had a little mistake at the last part of “Walk Forward Validation”
After showing us how to apply the model (the python code), you said :”In the above case, 2,820 models would be created and evaluated.”, which is not true, it is easly can be seen that 2320 (2820 – 500)/[n_train:n_records] models have been created.
Besides that, you gave here a satisfing explanation of some intuitive methods for replacing the well known ‘resampling methods’ from the classical machine learning, for uses onto TS data.
Thank you!
Absolutely right, thanks! Fixed.
Hello Jason,
here when you say train and test, do you actually mean train and validation ? since cross validation is done only on the training data whereby you split the entire training data into training and validation.
Thanks in advance.
I mean test, but you could use validation for the same function.
More here:
https://machinelearningmastery.com/difference-test-validation-datasets/
Thank you Jason,
So if I have a suite of models, example: Linear Regression, ridge, lasso, etc and I want to asses the performance of each in order to choose my final model can I do the following:??
1- split the time series data into 80% training and 20% testing
2- do walk forward validation on the 80% training
3- repeat (2) for all the models
4- choose the model with the best performance and evaluate now on the 20% testing ?
Many thanks in advance
Sounds great!
Thank you Jason! do you recommend nested cross validation (that internally implements walk forward validation) for time series ?
Example blog: https://towardsdatascience.com/time-series-nested-cross-validation-76adba623eb9
I don’t recommended any technique generally, but if you think it is appropriate for your problem, go for it.
Dr. Brownlee,
Especially in the case of Walk Forward Validation (but could also be addressed for multiple step forecasting), can you suggest the base way to prepare the training data and apply those preparations to the test set? Specifically, I’m referring to prep such as outlier treatment and normalization. Seems like you would need to prepare each new training set separately, which could be quite computationally expensive.
Thanks,
Jordan
Coefficients needed for data prep (e.g. min/max) would come from the initial training set.
Another approach would be to re-prepare data prior to each walk forward using all available obs.
I’ve been working on a flood forecast task training the model on LSTMs/GRU and even CNNs networks; I mostly was splitting the data in three sets: Train; Validation; and Test. The model always were overfitting. I’ve tried many things to improve it, but none worked.
However in one of my tries to improve the model, I mistakenly splitted the Train and Validation randomly, but test remained in the future; When I trained the model the results were greater than before and there were no overfit, as well both train and validation were improve together and at the end evaluating on test I was getting results as good as the validation and even better!
Since I did it the wrong way, why did it worked? Does it show that some periods of time are not correlated, thus the result did great instead of bad? I am really confused about the results since I did a mistake. One thing to note is that before doing the wrong splliting, the data was already in the 3D format, which means that the order of observations were preserved in the batches.
It may suggest that perhaps LSTM is not appropriate, that you were treating the LSTM like an MLP.
Perhaps try an MLP and compare results?
With time series splitting:
MPL model – The model doesn’t overfit neither does it improve. Both training and validation loss oscilates i.e goes up and down at every epoch.
LSTM model – The same as the MLP happens here.
Hybrid model (CONV-LSTM-DENSE) – Same thing
With randomly splitting :
MPL model – The training continuously improves, as well the validation but with oscilation. The model is overfitting.
LSTM model – Does well, the trainning and validation are always improving, there are a few oscilation in the validation loss. Validation performance decrease at the last epochs, where it start to overfit.
Hybrid model (CONV-LSTM-DENSE) – The model does very well. The loss of training and validation are always decreasing. There are some oscilations in the loss of validation. The model continuously improves and doesn’t overfit.
Nice work.
did u split the time series data sets train test with shuffle after making it supervised learning ?
Hi ! If I choose to use the expanding window, how do I build my model ? Should I build a RNN that could take inputs of different sizes (like 500,501,502…) or should i build one different model for each instance of that sequence ? If so, how can I compare those models?
Good question, I cover this in great detail here:
https://machinelearningmastery.com/start-here/#deep_learning_time_series
Hi, when i use the rolling window. how i will prepare my test set?
In the same way. Some of the train set might be needed for input to predict the first few steps of test.
It is easier to put all the data together, transform it, then split it.
Hi, Dr. Jason
I built a classifier for time series data (sequence-to-label classification) using unidirectional LSTM RNNs. At first I was dividing the data into 70% for training and 30% for testing using the ‘Holdout’ method, the results have been good (training accuracy = 99% and testing accuracy = 98%). And then I used k-fold cross validation, this led to the weakness of the model (training accuracy = 83% and testing accuracy = 83%), I realized that k-fold cross validation cannot be used with time series data, because it randomly divides the data into k-times, which affects their order. But the ‘Holdout’ method also divides data randomly and this affects the sequence of data, However gave good results. Knowing I didn’t use the shuffle.
I searched a lot and found no logical explanation for this difference.
Thanks in advance for help.
Train/Test split and CV are not appropriate for sequence data!
You must use walk-forward validation (described above).
Thanks Dr. Jason
Please, I want an explanation of the result of the Holdout method.
What do you mean exactly? Which part are you having trouble with?
My problem is that I found the ‘Holdout’ method give better results than the methods mentioned above even though it is a kind of CV.
What is the reason for this?
A train/test split and cross validation will be optimistic compared to walk forward validation.
A CV will shuffle observations randomly and give results form predicting the past given the future, e.g. a bad idea.
A train/test split is better, but may not test the model enough.
Thank you very much Dr. Jason
I searched a lot and finally reached a logical explanation. The Holdout method (Out-of-sample (OOS)) randomly divides the data with preserve the temporal order of observations. It deals well with real-world time series.
https://www.researchgate.net/publication/322586715_A_Comparative_Study_of_Performance_Estimation_Methods_for_Time_Series_Forecasting
Thanks for sharing.
Hi Dr. Jason
you’re welcome.
Dr. Jason, I have a simple question, when using the Multiple Train-Test Splits method, should I calculate the average value of accuracy? (For example in case 3 splits would be accuracy = (acc1 + acc2 + acc3)/3), or I take the accuracy of the last split?.
Thanks in advance for help.
Yes.
Thank you very much Dr. Jason
You’re welcome.
Thank you. Could you maybe do an article about multi-step predictions in time series? I’m super interested in the basic concepts… for example forecasting a year of shampoo sales, what would be the differences between 1 step forecasting in walk forward validation and multi step forecasting? When and why to choose one approach over the other?
Yes, there are many. You can start here:
https://machinelearningmastery.com/faq/single-faq/how-do-you-use-lstms-for-multi-step-time-series-forecasting
It is really easy with linear models, you just call forecast() with the number of steps needed.
The difference is walk-forward validation has access to more information.
Thanks, I think I have some basic problems connecting the dots here: I read your posts aboit using SARIMA as well as Exponential Smoothing algorithms (Holt Winters) for forecasting.
Both include an example where shampoo sales are forecasted based on monthly values. Are both algorithms/methods, that would fall under the “4. Multiple Oitput strategy” you described here https://machinelearningmastery.com/multi-step-time-series-forecasting/ ? From your answer I would guess so, but not sure.
Also both articles on SARIMA and Exponential Smoothing refer in their section about walk forward validation the ppssibility of doing a multi-step prediction within the cross validation.
I was wondering what would be the benefits/downsides of that? How to determine the step number (horizon) in the cross-validation? When do I choose multi-step over the 1-step walk forward validation? Should this mirror the predictopn timeframe I want to do with the fitted model?
I have a time series (4 years of monthly sales data) and want to predict the next 12 months. Currently I use the walk forward validation as described in your post about Exponential Smoothing. This has a horizon of 1 month. Since I want to forecast the next 12 months, would it be beneficial to expand the horizon to 12 months in the cross validation?
I hope it’s clear where I have troubles connecting the various information I found here. Your blog was really helpful for me. Thank you for that.
Good questions.
Yes, they can be used for a multi-output model, e.g. model.forecast(steps=10)
Yes, you can use walk-forward validation for multistep prediction, you can evaluate the model per step or across all steps.
You forecast the number of steps you need for your dataset, no more. The further you predict into the future, the worse the performance – predicting the future is hard!
Yes. Expand to 12 months and evaluate per future timestep or across all future time steps or both.
Does that help?
Yes, I think so. Thank you.
You’re welcome.
hi I need to know if I am predicting loan advances by weather condition per month and year would it be considered as a time series? my plan was just to verify the effect of the weather on loans
It sounds like time series.
Hi Jason,
I have a question about splitting time series data when you have multiple sources. In my use-case, I have multiple time series that I’m trying to use the same model for. For example, I am modeling sales predictions for a department in a store over time, and I have separate data for each department, and I am trying to create a central model that can predict the sales in any given department based on the past sales. I am currently splitting this up by using 70% of the departments as training sequences and 30% as testing sequences. I think that the equivalent of what you described in this article would be using the first 70% of all of the departments as the training sequences and the last 30% of all of the departments as the testing sequences. I am planning on trying both, but I am wondering if you think the former or latter is advisable?
Thanks!
Sounds like a good start.
This might also give you ideas:
https://machinelearningmastery.com/faq/single-faq/how-to-develop-forecast-models-for-multiple-sites
thank you!
HI Jason,
I have a question about the lifecycle of a model. Thanks to this tutorial I understand how to utilize TimeSeriesSplit on backtesting my model. I further expand this by creating a RandomForestClassifier with random_state=0 to return consistent results. I run through the loop saving the best model based on accuracy. Then I hyperparameter tune and save the best model. Finally, when it comes to prediction, would I use this saved model or would I instantiate a new RandomForestClassifier without random_state to harness the power of randomness? If the choice is the latter, why wouldn’t I go with the hyperparam tuned best model?
Thanks!
No, all testing is used to find the model/config. Those models are discarded. You then use the best model/config to fit a final model on all available data and start making predictions.
I explain more here:
https://machinelearningmastery.com/train-final-machine-learning-model/
Wow, thank you! Just to confirm: fitting on train/test data is just to quickly figure out if our ML algorithm is viable for the problem we are trying to solve. We can then take it further by using hyperparam tuning to figure out the model’s config. Then finally, to predict we set up a new model with those configs we found from hyperparam tuning.
Much appreciated.
Yes, this is the process outlined here:
https://machinelearningmastery.com/start-here/#process
Hi Jason,
I just have a question about shuffling the training data. From your article, I fully understand and learned (thanks for your sharing btw) that shuffling or applying cross-validation isn’t a good idea before splitting time series data. But what if after training test split? is it necessary and probably even essential to shuffle the training set after data splitting for time series data to avoid sequence bias?
Thank you for your answer in advance!
If you split the data, then shuffle the train set, that is fine – and might help stateless models operating on lag obs like most ml models.
Hi Jason,
How would I do walk forward validation with seasonal data? I need to walk forward in seasonal iterations (Spring, Summer, Fall, Winter), and each season contains thousands of rows.
Thanks
David
No difference.
Test the model under the same scheme you expect to use it.
Hola Jason, quería hacer una consulta, estoy realizando mi tesis y aplico series temporales. tengo data histórica mensual de 20 a’nos, la consulta es que la data que tengo ya devido en train y test y quiero utilizar el Walk Forward Validation, como aplico esto para que me vaya acumulando y vuela hacer así sucesivamente, por ejemplo si hago 10 divisiones.
– ? como seria el código en Python para que me divida, me acumule y vaya haciendo el Walk fordward validation?
– tengo entendido k el WFV se utiliza cuando solo tienes una sola variable en el tiempo, o se podría aplicar cuando se tiene varias variables y kiero evaluarlas a la vez en el tiempo, como aplicaría el WFV cuando tengo varias variables a la vez en el tiempo y como acumularía…..
Sounds like a great project.
There are many examples of walk-forward validation on the blog. Perhaps find one and adapt it for your project.
Yes, it applies for multivariate outputs and multi-step outputs. All cases.
Hi Jason!
Thanks for another great post.
There something I can’t completely understand…
Why can’t we turn it into classic ML problem where each sample input is let’s say fixed for 20 timestamps (t-20 to t0) and the response (or target) is the next value (t1) or later (multistep)?
when you break the data like that you would be able to use k-fold ?
If the model learns based on a sample from the future and predicts a sample from the past, the results will be optimistic and unreliable.
great tutorial!
How we can shuffle and surrogate time series data in R/Python. Please make a tutorial on it.
Shuffling time series data in a test harness would be invalid.
Hi Jason!
Regarding the problem of shuffling I don’t understand why would you shuffle time dependent data? That would make the time dependence disappear, right?
They do it here: https://www.tensorflow.org/tutorials/structured_data/time_series
Thanks!
Correct, it is a terrible idea generally.
Hi Jason!
Thanks for article. I have a question regarding sampled version of Walk-Forward validation. Let’s say i have some time series data where the last available data entries (with the latest timestamp) have greater importance for predictions on the test data. Is there any reasonable way how to do automated hyperparameter tuning on retraining? 🙁 I cannot easily split training data to get some validation subset for hyperparameter tuning. Choosing latest data as validation data will probably break model performance.
Thanks!
Typically the model will capture this relationship, and you can help by farming the problem as a supervised learning problem that only considers the most recent lagged observations:
https://machinelearningmastery.com/time-series-forecasting-supervised-learning/
Regarding a grid search with walk forward validation, see this:
https://machinelearningmastery.com/how-to-grid-search-sarima-model-hyperparameters-for-time-series-forecasting-in-python/
Hi Jason,
Great read. Thank you.
I was wondering. I have multiple related univariate timeseries in a set one after the other but each of the rows have supporting features (descriptions of the agent regarding the timeseries at hand). For each agent, I have generated lag windows within the row of some previous entries (7 days), and I have also added statistics such as mean and standard deviation pair-wise values of each day etc. in order to give the model more attributes to work with.
Since I have basically turned each entry in the timeseries as a ‘chunk’ with some previous data, is k-fold cross validation now a correct approach to use?
I have read quite a few papers that do this by generating temporal chunks of speech through the MFCCs of a time window and then use 10 fold cross validation, and I suppose I’m doing a similar thing with my series since each data object now also describes some previous steps in order to perform regression on the numerical output at step n.
My question is that, after this kind of lag-window and statistical transformation, is k-fold now an acceptable validation approach for a linear regression or neural network model with this data as input?
Thanks,
Jordan
Thanks!
You know your data better than me.
In general, no, if you train on the future and predict the past, the test is invalid.
Hi Jason,
Thank you! Great explanations like always.
I have one question relation to time-series prediction by skipping some data between the train and test.
Because today for example I am interested in forecasting 2 weeks (in a daily basis) but starting in 4 weeks.(skipping the next 4 weeks)
To cross-validate my model, I can’t just create my folds like:
Fold1: Train week 1 until week 10 and predict week 11,12
Fold2: Train week 1 until week 11 and predict week 12,13
and so on….
This split can’t give me an idea about the performance of the model. So I am creating my folds as follows:
Fold1: Train week 1 until week 10 skip 11,12,13,14 and predict week 15,16
Fold2: Train week 1 until week 11 skip 12,13,14,15 and predict week 16,17
and so on….
Is it the right way to cross-validate the model like that or do you suggest other ways?
Thanks in advance
Great question.
You MUST test the model under the conditions you expect to use it – whatever that happens to be.
Clear answer. Thanks ! 🙂
You’re welcome.
“It’s not valid to use cross validation for time series data, regression or classification. The train/test data must be split in such a way…”
With the case of time series classification, I have a hard time grasping your quote. I agree that the quote can apply to regression, but I don’t see how that can apply to classification. I understand that the feature values depend on the observation before it (temporal ordering), but in the end of the day, isn’t classification just taking different feature values and categorizing/splitting the values into a bucket? Therefore, we can ignore the temporal aspect of our data and randomly split our train/test sets.
Simple Binary Example to illustrate:
Feature1 target_variable
Day 1: 1 1
Day 2: 2 0
Day 3: 3 1
Day 4: 4 0
…
We can see that the ‘target_variable’ is 0 if even and 1 if odd. The feature data is in temporal order and each feature observation is dependent on the one before it (+1). But the models should still be able to pick up this pattern and classify it correctly. So whether we need to TimeSeriesSplit for our time series problem should be entirely up to the problem we are trying to solve? Thank you.
If you train on examples from the future your model will be invalid/optimistic, regardless of regression or classification.
I can’t thank you enough for your great articles but I pray for you with all the best, god bless you Dr. Brownlee.
Thanks!
Hey Jason, thank you for your amazing post.
I would like to better understand walk forward validation and sliding window approach. Do you have any source where you combine these two? In specific, do you have any example with MULTIVARIATE data?
Thank you and super appreciated your work!
Yes, perhaps start here:
https://machinelearningmastery.com/multivariate-time-series-forecasting-lstms-keras/
Hi Jason, Do you have any citations or references about Walk Forward Validation method over other validation methods for time-series?
So, I use LSTM in some experiments, but It is hard to explain because there is a clear separation from training/validation and test phases (split subset)
Not off hand, sorry. Any textbook on time series:
https://machinelearningmastery.com/books-on-time-series-forecasting-with-r/
Hello Jason. Thanks for the article.
I have one question just for know if I understood when to use sliding window and backtesting.
Backtesting is used for evaluate what model is the best for make a prediction and sliding windows is just a way to prepare the data for make the final prediction??
In other words, with a set data, first I make the backtesting with differents models and then I´ll make the final prediction with the best model using sliding windows, right??
Thank you.
Almost.
Sliding window is how we prepare the data for modeling, regardless of whether we are testing or using the model.
Backtesting is how we evaluate the model.
Dear Jason,
Thank you very much for the tutorial, it helps a lot for my project.
I have some questions regarding the multiple train splits and walk-forward validation.
Firstly, I applied the multiple train splits (with TimeSeriesSplit in python, n_splits = 10), but I noticed that the first few splits performed pretty badly, I assume it is because the number of the training data in the earlier splits is too small. Is this affecting the evaluation of the model performance?
Secondly, is walk-forward validation also applicable for multi-step forecasting with a direct approach where my output will be n_output >= 2 (I’m applying MLP, so n_output is my output node), where I would do for n_output = 2 as the following:
train: 500, test 2
train: 502, test 2
train: 504, test 2
….
Thank you very much in advance, I’m looking forward to your reply
best regards
I recommend using walk forward validation as a general rule.
Hi Jason,
Maybe I’m a bit slow, but I’m having a bit of trouble understanding how this all comes together. Regardless of whether it’s walk-forward validation, or temporal test-train splits, where does the data come from?
Say I have a time series like “abc def ghi jkl mno pqr s” with window size 3 and a 1 step prediction, and I split it as such:
train: “abcdefghi”
validation: “jklm”
test: “nopqrs”
and train it on windows “abc” to predict “d”, on “bcd” to predict “e”, … on “fgh” to predict “i”
For validation, do I use “ghi” to predict “j”, … up to “jkl” to predict “m”? Or do I just use “jkl” to predict “m” alone? That is, do I use the training data to predict values that lie in the validation data?
Similarly, for testing the model, do I first start with using “klm” to predict “n” and continue up to the end of the series (“pqr” to predict “s”) or do I start with the window “nop” to predict “q”?
With walk forward validation you would just have train and test, no val.
Hi Jason,
I see, thanks. How would I ensure that I don’t overfit the model to the test data, though?
Ensure the test dataset is sufficiently large and representative – this will give you confidence you are not overfitting.
Hi Jason,
Thank you for all of your blog posts they have been very helpful for a newcomer to machine learning like me.
However as a newcomer I get confused very easily so bear with me for what could be a stupid question.
I have been following your ‘Multivariate Time Series Forecasting with LSTMs in Keras’ tutorial and was trying to apply the Walk Forward Validation technique to that example. Therefore I replaced the train-test split used in that example with the Walk Forward loop as shown in this post and then shifted the the training and evaluation of the model into that walk forward loop.
The result of this is that I now have hundreds of models all with their own RMSE.
My question then is, am I meant to choose the model with the best RMSE from all those models reated in the Walk Forward validation or am I meant to somehow aggregate the models.
Kind Regards,
Harrison
You’re welcome.
Yes, for each model evaluated on the same walk-forward validation and data, choose the one that has the best skill and lowest complexity.
Hi Jason,
thanks for your all time great tutorials!
can we use both validation set to stop training at the point of over fitting, as well as walk-forward validation?
if possible can you show me how please.
You’re welcome.
Probably not. It does not sound appropriate off the cuff.
HI, First of All, Great Content, thanks.
Regarding feature optimization over the iterations, if we performance any kind of optimization in one iteration, do we keep it to the next ones?
An example, i start with all my features on the first iteration, if i learn from the results that some of them have little predictive value, do i keep them for the next iterations?
If you have additional reference of best practices on this topic of feature optmization, could you share?
Thanks in Advance.
Sorry, I don’t understand. Perhaps you could elaborate?
Hi Jason,
My concern is related to feature optimization from one Split iteration to the next.
Lets say, after training for Split N, i find that one or more features have little predictive value and i decide to take them out of the model for the Test Stage. Do i keep them out (excluded) for the next iterations on Split n+1, n+ 2,….. (Excluding a feature is just an example, the concern could be generalized for any Feature Engineering)
Or should i train every split iteration from Zero, with all features available and discarding any other feature optimization performed in previous splits?
Thanks
Justing adding steps that reflect my understanding.
Get all relevant data
Break data into multiple pieces
Run an optimisation to find the best parameters on the first piece of data (first in-sample)
Apply those parameters on the second piece of data (first out-of-sample)
Run an optimisation to find the best parameters on the next in-sample data
Apply those parameters on the next out-of-sample data
Repeat until you’ve covered all the pieces of data
Collate the performances of all the out-of-sample data
I think it better to start by selecting a metric to optimize, then define a test harness to evaluate models, then try a suite of dataprep/models/configs on the test harness to optimize your metric.
No, one treatment/model/config is evaluated in a consistent way on your test harness.
Thank you for your brilliant post, Jason!
Do you have any useful post/link on how to conduct FORWARD TESTING (e.g., using one-step ahead prediction to predict the next day, week, month?)
Thank you and keep smashing it!
Kevin
Yes, walk forward validation can do exactly this.
Yes, I know how to use walk forward validation for BACKTESTING (e.g., using 80% of data as training and 20% as testing, making the predictions one-step ahead over the testing data). However, I was wondering if you have an example where you show how to make predictions on new data (not matching the testing data)?
Thank you!
Kevin
The code is the same. Fit the model on all available data and call predict().
Perhaps this example will help:
https://machinelearningmastery.com/make-sample-forecasts-arima-python/
Hi Jason,
Your posts on framing a time series as a supervised learning problem as well as this post about backtesting machine learning models have been very informative for me.
I recently started learning machine learning and am currently working on predicting PM2.5 values using weather (Temperature, wind speed) and other correlated pollutants(NOx,CO…) as predictors. This is a multivariate time series dataset with an hourly frequency.
I want to frame this data as a supervised learning dataset. Based on the sliding window approach, I plan to add a number of lag variables for each variable. For predictions, I want to make hourly forecasts. Thus I was thinking of retraining models at each hourly step for the next forecast similar to the way you have described walk forward validation.
My question for you was if you see any flaws in this approach ? I ask as I am confused when you say that we need to choose either a sliding or expanding window whereas it seems I am using both.
As an example,
1. I plan to initially train on hourly data (say) Jan 1 2017, 12 am-Dec 31 2018, 11 pm,
2. Then make a prediction for Jan 1 2017 12 am.
3. And keep incorporating each subsequent hourly data point in the training set for model retraining and next step predictions.
Thanks.
No, sounds like a good approach. Prototype and test it, and compare to other approaches you can think of. This will help:
https://machinelearningmastery.com/how-to-develop-a-skilful-time-series-forecasting-model/
Thank you, that is helpful.
Also, a slightly related question, what do you think could be a reasonable way to deal with missing chunks in the time series data while applying walk forward validation ? I have a few missing patches and am currently imputing with the mean but not sure how good of a method that can be.
Good question, here are some suggestions:
https://machinelearningmastery.com/faq/single-faq/how-do-i-handle-discontiguous-time-series-data
Thank you.
Fantastic article as always. Question about downstream processes, probability thresholds, and parameter search:
Let’s say I’ve performed walk-forward validation on my data, and now I have a dataset of predictions for all validation sets.
Let’s say I have a downstream process that decides whether or not to take some action based on the “probability true” value.
Let’s say I create a program to search for the best “probability true” threshold value.
Do I need to split my time series data into “training” and “validation” sets for the optimal “probability true” parameter search? I’ve already done walk forward validation on the original training set. Do I also need to do walk forward validation for finding the best probability threshold in my downstream process?
Hmmm. Tough, things are getting complicated.
The threshold finding process must not be aware of the known value or of known values from the future. That’s a good start (requirement).
Perhaps you can hold the model constant, step forward with new data and use that to tune the threshold?
This is off the cuff. I think you might need to think hard about this and even prototype some ideas.
Jason is there anything wrong with a mult variate time series dataset without sliding window? For example my dataset is sub hourly building electricity (target variable) combined with weather data and time-of-week dummies. What I’m doing is for each time step (15 minutes) fitting the entire model with exception of the last row which is my test used to predict kW. Obviously offline process I am walking thru the entire years worth of data, fitting a model at each time step, and predicting out one step. comparing modeled kW to actual and the rsme really isn’t too bad. But I don’t think this is sliding window…
Not sure how you would train or validate the model.
Hi Jason, could the walk forward validation be enough to validate the model? For example the model would predict about a half years worth of hourly data (~3000 predictions, each prediction a new model was fitted) and I was comparing the rsme of the actual to predicted. Any tips greatly appreciated 🙂
Yes.
I used walk-forward validation in most of my deep learning for time series examples in the book and blog.
Is it also possible to use a statistics model (OLS multiple regression) to validate a machine learning model? If so what would be the process for that? Like would I run two separate walk forward validations with the same exact variables through a regression model prediction and also the machine learning model prediction… And then compare walk forward validation RSME’s between the statistics model & ML model? Curious if you think that would be a waste of time or not! Thanks Jason!
You can train an alternate model and compare performance. But it does not validate/invalidate another model, just provides a point of reference.
Yes, it is an excellent idea.
Shoot, I dont think I commented properly on your last message but I meant to comment on your:
Yes.I used walk-forward validation in most of my deep learning for time series examples in the book and blog.
Hi Jason. To increase the model fit speed, can we load weights obtained from the previous datasets to train with the next batch? Because I think that training a model every time and ignoring the previous weights is not optimal. At least we can use load the previous weights as the initial weight of the next model
Yes. Also see this:
https://machinelearningmastery.com/update-neural-network-models-with-more-data/
Hi Jason,
Thanks for all your work on ML, it’s really helpful.
I have one question regarding predictions inside a walk forward loop.
Let’s say we split the data as you did, for example train=2816, test=1 (just a single step inside the WF loop)
How do you make a prediction when the test set is only 1?
In other words, what should the input data be in model.predict function?
Sure, I can use last 100 (or n) observations from the train set as an input to predict the next timestep, but shouldn’t we test the model on unseen data?
The walk-forward validation case assumes we are making one step-predictions. You can make multi-step predictions if you prefer – there are many examples of this on the blog.
Thanks, but that’s not what I meant. I want to make one step prediction, but my concern is about the input data we pass into the predict function – shouldn’t it be different from the training data?
Generally, the model will take the last n time steps as input to predict t.
This does not have to be the case, you can design the prediction problem any way you want!
very very thnx for you..
You’re welcome.
Hi Jason,
I would like to make a persistence model for the forecast of a multivariate time series of the type multiple parallel input and multi-step output, honestly although I have the data very well organized for the case according to the series_to_supervised function, I have not been able to make a model of this style.
Could you please show me an example or tell me how I should make this model (except for the organization of the data because I already have that list according to the case).
Thank you for your attention, I am waiting for your answer.
Yes, there are many examples on the blog, perhaps start here:
https://machinelearningmastery.com/start-here/#deep_learning_time_series
Hi what if my train and test csv files are different, then how to use test file for prediction of the ime series values?
Fit your model on the training set and make predictions on the test set and compare the predicted values to the expected values.
Hello Jason!
Thanks for the numerous tutorials and great articles!
I used some of your tutorials as a basis to build my own CNN LSTM model for time series forecasting. My model is used to predict either the increase or decrease in alcohol consumption of the following day (classification model) or the absolute value of alcohol consumption of the following day.
While designing the model, I have of course already come across the terms “Sliding Window” or “Expanding Window” and now apply a Window of 21 days, with a Stride of 1, to make my predictions – as I understand this has nothing to do with backtesting.
Nevertheless, somehow the whole thing already sounds very similar to backtesting to me, or am I wrong? I’m not quite sure whether I afterwards would have to generate another window for backtesting (in a larger frame) and then apply this over the whole model. Would the window used in the model then simply be used in the larger window of the backtesting? For example, a 21-day window in the model in a 500-day window for backtesting?
In my model I also use a train-validation split of 90 to 10%, I then need the size information of the training split for the definition of the input_shape in the cnn model. If using backtesting, would this information somehow be omitted, or would it simply have to be adjusted again and again during each backtesting window adjustment?
In all the tutorials on backtesting that I have read so far, they simply create a very simple model that is then repeatedly fitted in a for loop. However, my model is composed of different parts and I somehow lack the knowledge of how to bring the whole thing into a backtesting framework… Unfortunately, there is rather limited help online. Do you know of any tutorials where backtesting is done with a CNN-LSTM model? That would be a great help for me!
Anyway, thanks a lot for the great help I already received from you 🙂
You’re welcome.
A sliding window is a type of backtesting. It is called walk-forward validation when used on new data each slide.
Not sure if that answers your question.
Thanks for the quick reply!
But doesn’t a CNN or LSTM always use a window in some way to go over the data?
For example in your blog entry https://machinelearningmastery.com/how-to-develop-rnn-models-for-human-activity-recognition-time-series-classification/ you combine a LSTM and CNN model. You write “Note, it is common to not shuffle sequence data when fitting an LSTM. Here we do shuffle the windows of input data during training (the default). In this problem, we are interested in harnessing the LSTMs ability to learn and extract features across the time steps in a window, not across windows.”.
Does this window have something to do with backtesting? As i understand it is simply a method for training the model and not for evaulating it.
Yes, where each batch or even the entire training set is an ordered list of samples (windows).
Yes, we use walk-forward validation to evaluate models of this type.
thanks again for the super fast reply… and sorry for being so slow, I just find it difficult to grasp.
those “ordered list of samples” have nothing to do with backtesting in general?
No, the fact that samples are ordered is critical to the definition of the problem and to the way we train/test/evaluate models. If we train on the future and predict on the past, the model is invalid.
Dear Jason,
Thanks so much for this in-depth post. I wonder if you could elaborate on the use of LOOCV on the subject level (LOSOCV) for deep learning models in classification tasks. For example, the use of LOSOCV to train a CNN-LSTM model to classify subjects as healthy controls or dementia patients based on their EEG data (or any other time series data).
Thank you.
Rahul.
What is “LOSOCV”?
Hi Jason,
I’ve been reading your content for some time now while trying to learn how to program Machine Learning using Python. It has been helpful.
I’m not sure if this is a coincidence or not, but I found that using walk-forward validation when compared to my original data, there is a shift to the right (original data is trained, and the shift is the tested data).
The results look pretty accurate if I were to shift it to the left, but I’m not sure if that was intended or not. Could you share your insight? Is it because it is a “walk-forward” that it’s “shifted”?
Good question, see this:
https://machinelearningmastery.com/faq/single-faq/why-is-my-forecasted-time-series-right-behind-the-actual-time-series
Hello Jason, thanks for your great help on many titles,
In order to compare multiple forecasting models, I use walk forward cross-validation with expanding window on 20 different datasets and note the average errors(MAE or RMSE), and create boxplots. These datasets belong to different devices and, using them I am optimizing the hyperparameters. On the test side, I am a little bit confused. I have another group of 20 datasets. With the same hyperparameters, is it a good way to make the test on these secondary groups of datasets the same way (cross-validate which include training and validation again) and generate error metrics again, or use another way?
Best regards
Once you confirmed about your hyperparameters, you train your model again, and use your test set to evaluate it to get a sense of how it works for new data. You don’t need to cross validate again. But use your test set as a confirmation that your model is a good one.
Hi Jason,
Assuming you have to interpolate missing values in your time series, would you do this in the same way for both your train and test sets to backtest? Generally for testing an ML model imputation should not be done using test set data but not sure how this applies when interpolating time series data?
Time series imputation can either be interpolation, or copy-over like “back-fill” or “forward-fill”. These methods have no parameters to calibrate and hence should work just well for training and test data. Filling missing value as average, however, need to be very careful for what average means and often is not a good approach for time series.
Thanks Adrian for your reply. Would you check how accurate interpolation/other imputation methods are for your test set? For example interpolate for periods of time where you have actual data to see if it gives good results, otherwise you may be introducing bad data into your test set which will give misleading validation of a time series model?
I believe there is something you need to check with your particular dataset. Can’t possibly say it is accurate or not in general. Decisions like this usually needs justification to prove why it is a good idea.
Just to add to the article, the timeseries split functionality is now offered by sklearn as you may find it here
https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.TimeSeriesSplit.html
Hello Jason,
I have being reading your articles since 2 years Jason, They have helped me quite a lot.
I also would like to know whether there is a code example that contains sliding window example as I have been struggling to start working on this for months.
Appreciate any help and advice on this, thank you.
Hi Cel…I would highly recommend the following resource for better understanding:
https://machinelearningmastery.com/introduction-to-time-series-forecasting-with-python/
Hi Jason,
I’m not sure about thing. If we cant to tune a model based on walk forward validation. A train-test split is enough to tune the hyperparameters and test the model? Ignoring the validation split that is usually used in ANN models.
Thanks a lot for all your content, is a great help.
Thank you for the feedback J.Llop! I am not sure I understand your question. Could you clarify so that I may be better assist you?
Sorry I did not see your response and asked again on other question.
I mean that I’m tuning the hyperparameters of a LSTM doing walk forward validation(WFV). So I have split the dataset in train and test data.
Because from what I understood, doing WFV is not necessary to do a train-validation-test splits. I’m skipping the creation of a validation set between the train and test time series, so the test results, I get doing the WFV are the ones I’m using at the end for comparing to other models.
But it is strange to me, because it makes me think that the model could overfit, without the existance of a validation set itself.
So it is enough to do a WFV with train-test split, and grid searching the parameters during it, or is it necessary to:
-make a train-validation-test split,
-tune the parameters making a WFV with the train-validation sets
-test the model with a WFV with the train-validation sets
Thank you in advance!
Hi J.LLOP…The following will provide more clarity on how to avoid overtraining.
https://machinelearningmastery.com/early-stopping-to-avoid-overtraining-neural-network-models/
Hi James, I review it but there is something I miss when applied to time series forecasting.
If we are using walk-forward validation. Can we tune the hyperparameters with a train-test split using this technique along?
Or is it necessary to make a walk-forward validation between train-validation sets for tuning hyperparameters. And then test the results with a walk-forward validation between train(previous train + validation) – test splits.
Could you resume the process for train-validation-test splits when tuning time series forecasting?
I checked one post you have tuning LSTM but there you only have train-test splits.
Is it to assume that we have an other test split reserved for testing results once the hyperparameter is finished?
The thing is in my model, I do a train-test split and walk forward validation, and I tune the hyperparameters on that splits. So the final results I get (rmse…) are also based on that one, I don’t have any data reserved, so I don’t know if I could overfit, or it is something walk-forward validation avoids because is different to regular k-fold cross validation techniques.
Thanks so much for your help
Hi J.LLOP…The following article does a great job of explaining the benefits of walk forward validation. While it does help as stated below, you should always perform validation against unseen data to ensure that overfitting is not occurring.
“By using Walk Forward Validation approach, we in fact reduce the chances overfitting issue because it never uses data in the testing that was used to fit model parameters. At the same time, this approach allows to take full advantage of the data by using as much of the data as possible to fit and to test the models. However, though walk-forward is most preferred for statistical models; for ML, the improved estimate comes at the computational cost when we are creating so many models. This could be an issue at scale in case of large dataset.”
(Retrieved from https://sarit-maitra.medium.com/take-time-series-a-level-up-with-walk-forward-validation-217c33114f68#:~:text=By%20using%20Walk%20Forward%20Validation,and%20to%20test%20the%20models. on January 20, 2022)
I already write you back, but a simple question would be:
I bought the book “Deep Learning for Time Series Forecasting – Jason Brownlee” and followed the V chapter (Multi-step Forecasting) to make a grid search framework.
The walk-forward validation makes sure the results are not over-fit or do we have to run other tests for that?
Thanks a lot in advance
Hi Jason,
I’m not sure about something. If we want to tune (hyperparameters, such as LSTM) a model based on walk forward validation. A train-test split is enough to tune the hyperparameters and test the model as well? Ignoring the validation split that is usually used in ANN models (based on cross validation).
I mean, could I use the train-test split and make walk forward validation for testing the model while I am choosing the best model, skipping a validation set itself.
Thanks a lot for all your content, is a great help.
Your comment is awaiting moderation.
Hi Jason,
Thankyou for all the insight that your blog posts have provided. Very useful indeed.
I’m preparing data for LSTM time series forecasting as follows:
1. Create sliding window to get Tx (32 in this case) input datapoints for each sample. And then looking to a future timestep for the label. Pretty standard. I’m moving the sliding window one timestep forward to get the next set of input/output data.
2. Then I’m shuffling and splitting the X and y to get train, val and test sets.
So, the train, val and test sets are a collection of windowed samples taken randomly from the entire dataset. But in the process of doing so I fear that due to the ‘overlap’ of the windows that there will be leakage of information from val and test back to the training data.
Q) If you’re with me so far, could you advise whether that would be the case?
I think your suggestion is: Given a 60:20:20 pct split, to take the fist 60% of data over time as training data, the next 20% as validation and the most recent 20% as test, and then generate three sets of sliding window samples from those splits.
Q) Would you shuffle the prepared train data before training?
Q) While this approach eliminates leakage would it be sensitive to non-stationary data such as closing prices of a stock?
Hi Nigel…Time series data should not be altered or shuffled so as to maintain the autocorrelation properties that the LSTM is able to determine.
Hi James,
Thank you for your reply.
Just to clarify, I’m creating the sequence of ordered timesteps and labels before shuffline. That is, my LSTM input is [m, Ty, n] where:
m – number of samples
Ty – number of timesteps
n – number of features
The Ty are contiguous measurements ‘windowed’ from the timeseries before shuffling. It’s the samples m which are shuffled and then split into Train, Val and Test.
Despite that, should I still not shuffle the data at all and feel the samples into the LSTM ‘in order’ that they were taken from the time series data?
Hi James,
Thank you for your reply.
Just to clarify, I’m creating the sequence of ordered timesteps and labels before shuffline. That is, my LSTM input is [m, Ty, n] where:
m – number of samples
Ty – number of timesteps
n – number of features
The Ty are contiguous measurements ‘windowed’ from the timeseries before shuffling. It’s the samples m which are shuffled and then split into Train, Val and Test.
Despite that, should I still not shuffle the data at all and feel the samples into the LSTM ‘in order’ that they were taken from the time series data?
Hi James
Suppose that i will implement a loop to manage backtest with only one instance to test and training growing at each step (split many samples)
What about the training / fitting of the model (sequential model in Keras), shall we keep the fitting without recompiling new model etc…
Hi Rimitti…the following may help with updating models.
https://machinelearningmastery.com/update-neural-network-models-with-more-data/
Hello, I am a bit late to reading this but thank you. I am trying to choose between multiple time-series models using walk forward analysis. One is the clear winner in the trained dataset, and another is the clear winner in the untrained dataset. How do I determine which is better? Should I also consider variation between each phase and/or amount of degradation from trained performance to untrained performance? I appreciate your thoughts!
Hi Steve…you choose the model that performs best on data never seen during training. This is the “validation dataset”.
Well I am bit cofused can you just help me understand the basic difference between multiple train test split and wak forward validation
Hi Wazo…The following may be of interest to you:
https://machinelearningmastery.com/train-test-split-for-evaluating-machine-learning-algorithms/
In cross-validation with 10 iterations, we can say 10-fold cross-validation. How does walk forward validation with 10 iterations? Can we say too that 10-fold walk-forward validation?
Hi Jason, thanks a lot for this post. Really!!
So, let me see if I understood it well.
1) This is about validating your model so that you get to know if it is overfitted or not before checking the test set (which I should only evaluate few times), right? So, let’s say I validated and selected my model and I want to make the out of sample forecasts in the test set. If I ran several models in a rolling training window, how should the predict() command work? Should it select the latest training model coefficients (let’s think of a linear regression to make it simple)?
Or 2) should I again fit a new model in the test set to use more recent data and then make the prediction 1 step ahead? (assuming that I have already selected the model type/config when validating in the training set).
2.1) Initially I thought that the test set should never be fitted, but thinking more about the real unkown data
that I will have to make forecasts in the real world, I would like to use recent data to get my model
coefficients.
Many Thanks in advance,
Isadora
Hi Jason,
I have the following setup:
Classification task to predict 0, 1
Features: time series
I would like to backtest the trading strategy, therefore will use expanding window cross validation (you call it walk forward cross val).
However I would like to tune hyperparameters for each model as realistically I would need to do so in production, so the backtest should reflect it.
Therefore, could you tell me if this approach is correct:
Train data on the initial window, tune hyperparameters using consecutive window of data as validation.
Pick best parameters.
Retrain data on train+validate and
Take yet another consecutive window as test.
Move along by 1 data point and re-do.
Get average performance over test data sets.
So say t_1 to t_1000 is initial window. Train on that and try different hyperparameters and check which one is best on validation data which is t_1001 to t_1051. Then pick best hyperparam, retrain model on train+validate, and test on t_1052 to t_1053.
Next question is about production (i.e. final model).
Once I got the estimate of my algorithm’s skill, I need to obtain the final model.
Shall I take all data and split it into train + validation e.g. train t_1 to t_5000 and validate t_5001 to t_5500.
Tune hyperparameters using the validation set thus establishing best final model.
Then combine all data and fit the model using the found hyperparameters.
Hello, thanks for the amazing job you do. I would like to know if it’s a good idea to visualize a curve like learning curve while using walk forward validation. My idea is to plot the loss obtained in each split against the consecutive number of split or the sequence variable. This will explain how loss behave while the model advance trough the splits. Does this make any sense to you? Could this be use as an alternative to learning curve?
Hi David…You are very welcome! Your idea is very interesting. Please share the results of the implementation of your idea.